|
Plane Wave
In physics Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ..., a plane wave is a special case of a wave or field: a physical quantity whose value, at any given moment, is constant through any plane that is perpendicular to a fixed direction in space. For any position \vec x in space and any time t, the value of such a field can be written as F(\vec x,t) = G(\vec x \cdot \vec n, t), where \vec n is a unit-length vector, and G(d,t) is a function that gives the field's value as dependent on only two real parameters: the time t, and the scalar-valued displacement d = \vec x \cdot \vec n of the point \vec x along the direction \vec n. The displacement is constant over each plane perpendicular to \vec n. The values of the field F may be scalars, vectors, or any other physical or ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." It is one of the most fundamental scientific disciplines. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics. (...) You will come to see physics as a towering achievement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Wiley (publisher)
John Wiley & Sons, Inc., commonly known as Wiley (), is an American multinational publishing company that focuses on academic publishing and instructional materials. The company was founded in 1807 and produces books, journals, and encyclopedias, in print and electronically, as well as online products and services, training materials, and educational materials for undergraduate, graduate, and continuing education students. History The company was established in 1807 when Charles Wiley opened a print shop in Manhattan. The company was the publisher of 19th century American literary figures like James Fenimore Cooper, Washington Irving, Herman Melville, and Edgar Allan Poe, as well as of legal, religious, and other non-fiction titles. The firm took its current name in 1865. Wiley later shifted its focus to scientific, technical, and engineering subject areas, abandoning its literary interests. Wiley's son John (born in Flatbush, New York, October 4, 1808; died in East ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Rectilinear Propagation
Rectilinear propagation describes the tendency of electromagnetic waves (light) to travel in a straight line. Light does not deviate when travelling through a homogeneous medium, which has the same refractive index throughout; otherwise, light experiences ''refraction''. Even though a wave front may be bent, (e.g. the waves created by a rock hitting a pond) the individual rays are moving in straight lines. Rectilinear propagation was discovered by Pierre de Fermat. Rectilinear propagation is only an ''approximation''. The rectilinear approximation is only valid for short distances, in reality light is a wave and have a tendency to spread out over time. The distances for which the approximation is valid depends on the wavelength and the setting being considered. For everyday usages, it remains valid as long as the refractive index in the medium is constant. The more general theory for how light behaves is described by Maxwell's equations. Proof Take three cardboard A, B and C, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Plane-wave Expansion
In physics, the plane-wave expansion expresses a plane wave as a linear combination of spherical waves: e^ = \sum_^\infty (2 \ell + 1) i^\ell j_\ell(k r) P_\ell(\hat \cdot \hat), where * is the imaginary unit, * is a wave vector of length , * is a position vector of length , * are spherical Bessel functions, * are Legendre polynomials, and * the hat denotes the unit vector. In the special case where is aligned with the ''z'' axis, e^ = \sum_^\infty (2 \ell + 1) i^\ell j_\ell(k r) P_\ell(\cos \theta), where is the spherical polar angle of . Expansion in spherical harmonics With the spherical-harmonic addition theorem the equation can be rewritten as e^ = 4 \pi \sum_^\infty \sum_^\ell i^\ell j_\ell(k r) Y_\ell^m(\hat) Y_\ell^(\hat), where * are the spherical harmonics and * the superscript denotes complex conjugation. Note that the complex conjugation can be interchanged between the two spherical harmonics due to symmetry. Applications The plane wave expansio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the rate that the vector field alters the volume in an infinitesimal neighborhood of each point. (In 2D this "volume" refers to area.) More precisely, the divergence at a point is the rate that the flow of the vector field modifies a volume about the point ''in the limit'', as a small volume shrinks down to the point. As an example, consider air as it is heated or cooled. The velocity of the air at each point defines a vector field. While air is heated in a region, it expands in all directions, and thus the velocity field points outward from that region. The divergence of the velocity field in that region would thus have a positive value. While the air is cooled and thus contracting, the divergence of the velocity has a negative value. Physical interpretation of divergence In physical terms, the divergence of a vector field is the extent to which the vector fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Gradient
In vector calculus, the gradient of a scalar-valued differentiable function f of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p gives the direction and the rate of fastest increase. The gradient transforms like a vector under change of basis of the space of variables of f. If the gradient of a function is non-zero at a point p, the direction of the gradient is the direction in which the function increases most quickly from p, and the magnitude of the gradient is the rate of increase in that direction, the greatest absolute directional derivative. Further, a point where the gradient is the zero vector is known as a stationary point. The gradient thus plays a fundamental role in optimization theory, where it is used to minimize a function by gradient descent. In coordinate-free terms, the gradient of a function f(\mathbf) may be defined by: df=\nabla f \cdot d\mathbf where df is the total infinitesimal change in f for a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Linear Operator
In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a mapping V \to W between two vector spaces that preserves the operations of vector addition and scalar multiplication. The same names and the same definition are also used for the more general case of modules over a ring; see Module homomorphism. If a linear map is a bijection then it is called a . In the case where V = W, a linear map is called a linear endomorphism. Sometimes the term refers to this case, but the term "linear operator" can have different meanings for different conventions: for example, it can be used to emphasize that V and W are real vector spaces (not necessarily with V = W), or it can be used to emphasize that V is a function space, which is a common convention in functional analysis. Sometimes the term ''linear function'' has the same meaning as ''linear map' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Local Operator
Local may refer to: Geography and transportation * Local (train), a train serving local traffic demand * Local, Missouri, a community in the United States Arts, entertainment, and media * ''Local'' (comics), a limited series comic book by Brian Wood and Ryan Kelly * ''Local'' (novel), a 2001 novel by Jaideep Varma * ''The Local'' (film), a 2008 action-drama film * ''The Local'', English-language news websites in several European countries Computing * .local, a network address component Mathematics * Local property, a property which occurs on ''sufficiently small'' or ''arbitrarily small'' neighborhoods of points * Local ring, type of ring in commutative algebra Other uses * Pub, a drinking establishment, known as a "local" to its regulars See also * * * Local group (other) * Locale (other) * Localism (other) * Locality (other) * Localization (other) * Locus (other) * Lokal (other) Lokal may refer t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
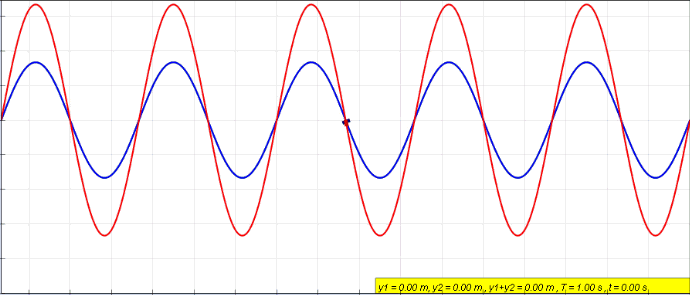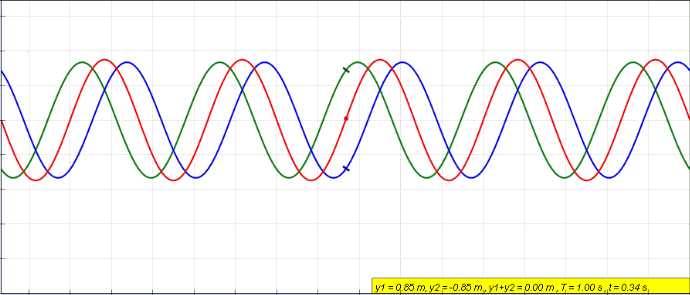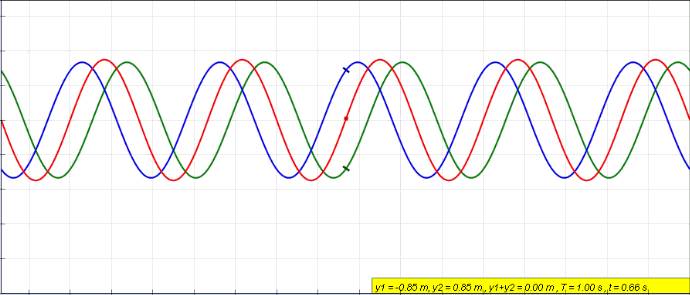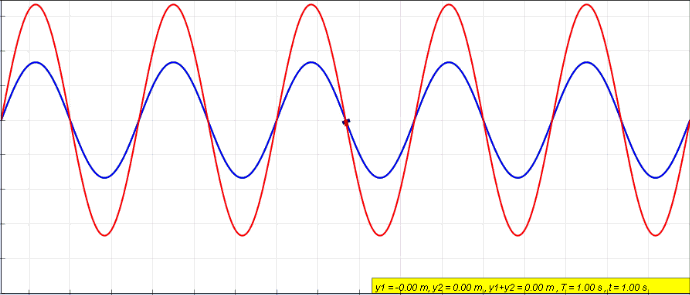
Plane Standing Wave
Plane most often refers to: * Aero- or airplane, a powered, fixed-wing aircraft * Plane (geometry), a flat, 2-dimensional surface * Plane (mathematics), generalizations of a geometrical plane Plane or planes may also refer to: Biology * Plane (tree) or ''Platanus'', wetland native plant * ''Planes'' (genus), marsh crabs in Grapsidae * '' Bindahara phocides'', the plane butterfly of Asia Maritime transport * Planing (boat), where weight is predominantly supported by hydrodynamic lift * ''Plane'' (wherry), a Norfolk canal boat, in use 1931–1949 Music *"Planes", a 1976 song by Colin Blunstone *"Planes (Experimental Aircraft)", a 1989 song by Jefferson Airplane from ''Jefferson Airplane'' *" Planez", originally "Planes", a 2015 song by Jeremih *"The Plane", a 1987 song on the '' Empire of the Sun'' soundtrack *"The Plane", a 1997 song by Kinito Méndez Other entertainment * Plane (''Dungeons & Dragons''), any fictional realm of the D&D roleplaying game's multiverse * ''Pla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Standing Wave
In physics, a standing wave, also known as a stationary wave, is a wave that oscillates in time but whose peak amplitude profile does not move in space. The peak amplitude of the wave oscillations at any point in space is constant with respect to time, and the oscillations at different points throughout the wave are in phase. The locations at which the absolute value of the amplitude is minimum are called node (physics), nodes, and the locations where the absolute value of the amplitude is maximum are called antinodes. Standing waves were first described scientifically by Michael Faraday in 1831. Faraday observed Faraday wave, standing waves on the surface of a liquid in a vibrating container. Franz Melde coined the term "standing wave" (German: ''stehende Welle'' or ''Stehwelle'') around 1860 and demonstrated the phenomenon in his classic experiment with vibrating strings. This phenomenon can occur because the medium is moving in the direction opposite to the movement of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Light Wave
In physics, electromagnetic radiation (EMR) is a self-propagating wave of the electromagnetic field that carries momentum and radiant energy through space. It encompasses a broad spectrum, classified by frequency or its inverse, wavelength, ranging from radio waves, microwaves, infrared, visible light, ultraviolet, X-rays, and gamma rays. All forms of EMR travel at the speed of light in a vacuum and exhibit wave–particle duality, behaving both as waves and as discrete particles called photons. Electromagnetic radiation is produced by accelerating charged particles such as from the Sun and other celestial bodies or artificially generated for various applications. Its interaction with matter depends on wavelength, influencing its uses in communication, medicine, industry, and scientific research. Radio waves enable broadcasting and wireless communication, infrared is used in thermal imaging, visible light is essential for vision, and higher-energy radiation, such as X-rays ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
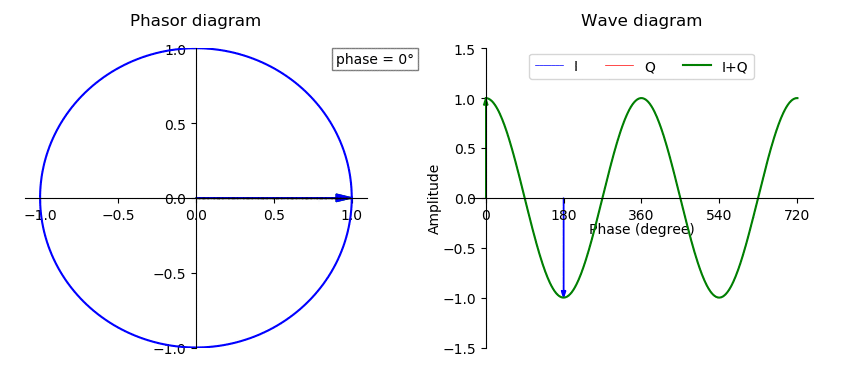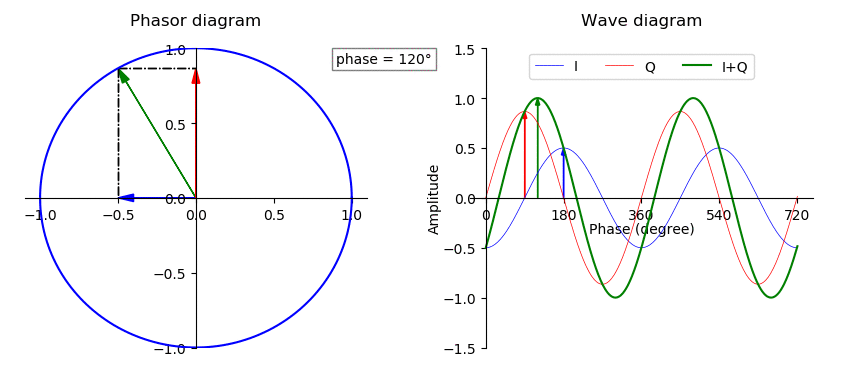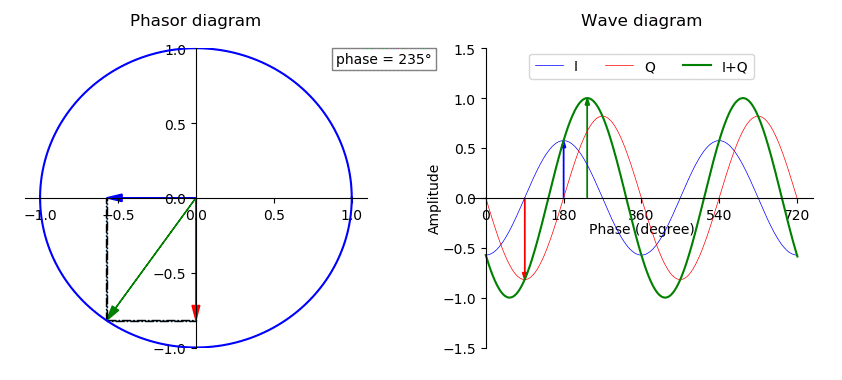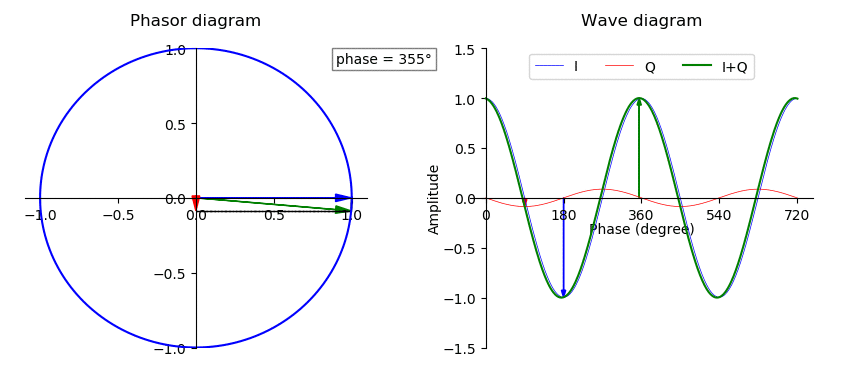
Phase Shift
In physics and mathematics, the phase (symbol φ or ϕ) of a wave or other periodic function F of some real variable t (such as time) is an angle-like quantity representing the fraction of the cycle covered up to t. It is expressed in such a scale that it varies by one full turn as the variable t goes through each period (and F(t) goes through each complete cycle). It may be measured in any angular unit such as degrees or radians, thus increasing by 360° or 2\pi as the variable t completes a full period. This convention is especially appropriate for a sinusoidal function, since its value at any argument t then can be expressed as \varphi(t), the sine of the phase, multiplied by some factor (the amplitude of the sinusoid). (The cosine may be used instead of sine, depending on where one considers each period to start.) Usually, whole turns are ignored when expressing the phase; so that \varphi(t) is also a periodic function, with the same period as F, that repeatedly sc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |