|
Pipe Surface
In geometry and topology, a channel or canal surface is a surface formed as the envelope of a family of spheres whose centers lie on a space curve, its '' directrix''. If the radii of the generating spheres are constant, the canal surface is called a pipe surface. Simple examples are: * right circular cylinder (pipe surface, directrix is a line, the axis of the cylinder) * torus (pipe surface, directrix is a circle), * right circular cone (canal surface, directrix is a line (the axis), radii of the spheres not constant), * surface of revolution (canal surface, directrix is a line), Canal surfaces play an essential role in descriptive geometry, because in case of an orthographic projection Orthographic projection (also orthogonal projection and analemma) is a means of representing Three-dimensional space, three-dimensional objects in Two-dimensional space, two dimensions. Orthographic projection is a form of parallel projection in ... its contour curve can be drawn as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torus
In geometry, a torus (plural tori, colloquially donut or doughnut) is a surface of revolution generated by revolving a circle in three-dimensional space about an axis that is coplanar with the circle. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a spindle torus. If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid. Real-world objects that approximate a torus of revolution include swim rings, inner tubes and ringette rings. Eyeglass lenses that combine spherical and cylindrical correction are toric lenses. A torus should not be confused with a '' solid torus'', which is formed by r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Implicit Surface
In mathematics, an implicit surface is a surface in Euclidean space defined by an equation : F(x,y,z)=0. An ''implicit surface'' is the set of zeros of a function of three variables. ''Implicit'' means that the equation is not solved for or or . The graph of a function is usually described by an equation z=f(x,y) and is called an ''explicit'' representation. The third essential description of a surface is the '' parametric'' one: (x(s,t),y(s,t), z(s,t)), where the -, - and -coordinates of surface points are represented by three functions x(s,t)\, , y(s,t)\, , z(s,t) depending on common parameters s,t. Generally the change of representations is simple only when the explicit representation z=f(x,y) is given: z-f(x,y)=0 (implicit), (s,t,f(s,t)) (parametric). ''Examples'': #The plane x+2y-3z+1=0. #The sphere x^2+y^2+z^2-4=0. #The torus (x^2+y^2+z^2+R^2-a^2)^2-4R^2(x^2+y^2)=0. #A surface of genus 2: 2y(y^2-3x^2)(1-z^2)+(x^2+y^2)^2-(9z^2-1)(1-z^2)=0 (see diagram). #The su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
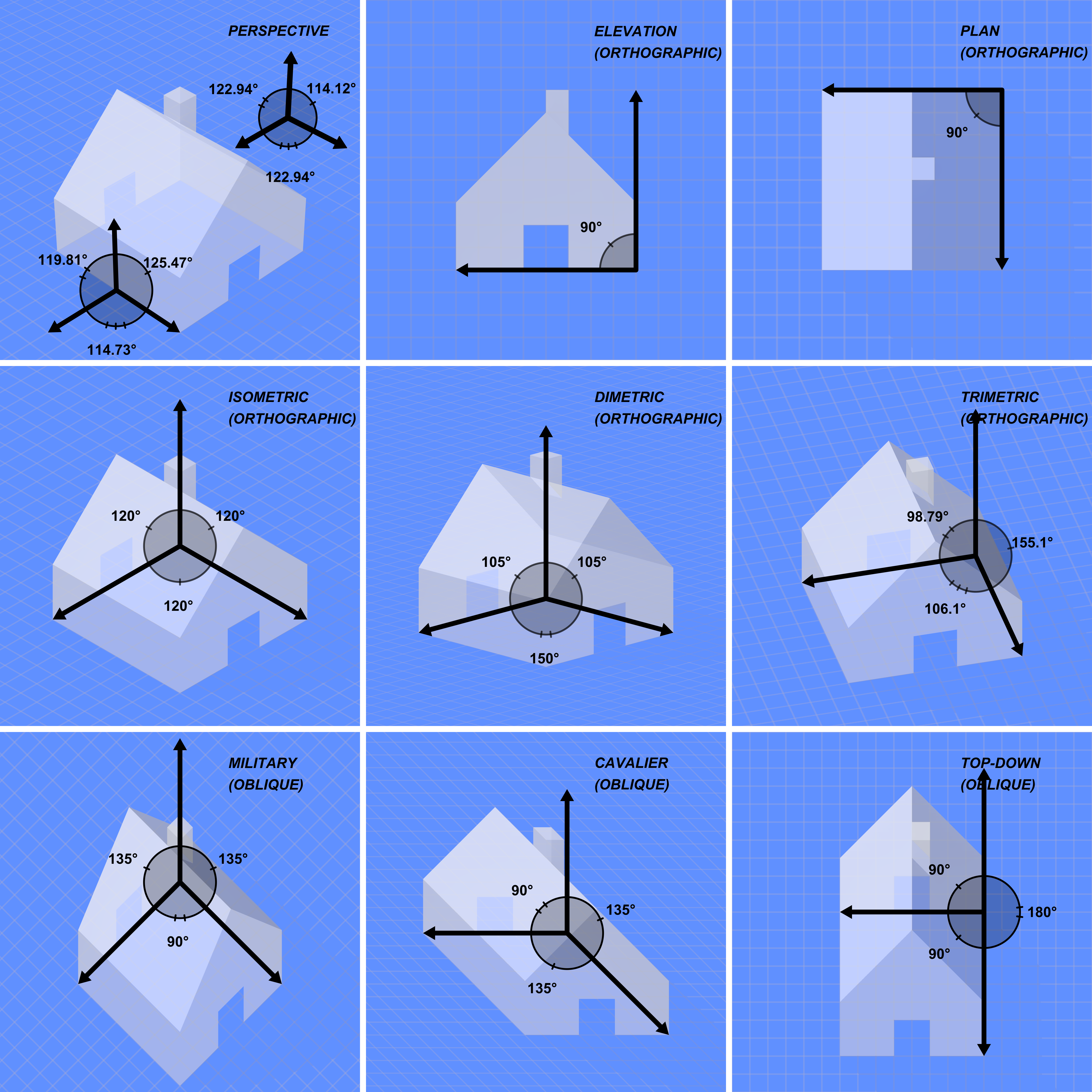
Orthographic Projection
Orthographic projection (also orthogonal projection and analemma) is a means of representing Three-dimensional space, three-dimensional objects in Two-dimensional space, two dimensions. Orthographic projection is a form of parallel projection in which all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface. The obverse of an orthographic projection is an oblique projection, which is a parallel projection in which the projection lines are ''not'' orthogonal to the projection plane. The term ''orthographic'' sometimes means a technique in multiview projection in which principal axes or the planes of the subject are also parallel with the projection plane to create the ''primary views''. If the principal planes or axes of an object in an orthographic projection are ''not'' parallel with the projection plane, the depiction is called ''axonometric'' or an ''auxiliary views''. (''A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Of Revolution
A surface of revolution is a surface in Euclidean space created by rotating a curve (the generatrix) around an axis of rotation. Examples of surfaces of revolution generated by a straight line are cylindrical and conical surfaces depending on whether or not the line is parallel to the axis. A circle that is rotated around any diameter generates a sphere of which it is then a great circle, and if the circle is rotated around an axis that does not intersect the interior of a circle, then it generates a torus which does not intersect itself (a ring torus). Properties The sections of the surface of revolution made by planes through the axis are called ''meridional sections''. Any meridional section can be considered to be the generatrix in the plane determined by it and the axis. The sections of the surface of revolution made by planes that are perpendicular to the axis are circles. Some special cases of hyperboloids (of either one or two sheets) and elliptic paraboloids are su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
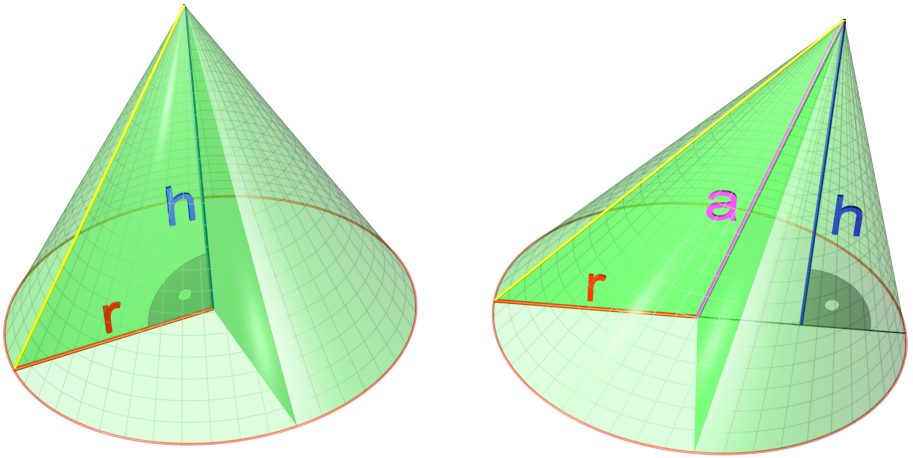
Right Circular Cone
A cone is a three-dimensional geometric shape that tapers smoothly from a flat base (frequently, though not necessarily, circular) to a point called the apex or vertex. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base that is in a plane that does not contain the apex. Depending on the author, the base may be restricted to be a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is a two-dimensional object in three-dimensional space. In the case of a solid object, the boundary formed by these lines or partial lines is called the ''lateral surface''; if the lateral surface is unbounded, it is a conical surface. In the case of line segments, the cone does not extend beyond the base, while in the case of half-lines, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Right Circular Cylinder
A cylinder (from ) has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base. A cylinder may also be defined as an infinite curvilinear surface in various modern branches of geometry and topology. The shift in the basic meaning—solid versus surface (as in ball and sphere)—has created some ambiguity with terminology. The two concepts may be distinguished by referring to solid cylinders and cylindrical surfaces. In the literature the unadorned term cylinder could refer to either of these or to an even more specialized object, the ''right circular cylinder''. Types The definitions and results in this section are taken from the 1913 text ''Plane and Solid Geometry'' by George Wentworth and David Eugene Smith . A ' is a surface consisting of all the points on all the lines which are parallel to a given line and which pass through a fixed plane curve in a p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generatrix
In geometry, a generatrix () or describent is a point, curve or surface that, when moved along a given path, generates a new shape. The path directing the motion of the generatrix motion is called a directrix or dirigent. Examples A cone can be generated by moving a line (the generatrix) fixed at the future apex of the cone along a closed curve (the directrix); if that directrix is a circle perpendicular to the line connecting its center to the apex, the motion is rotation around a fixed axis and the resulting shape is a circular cone. The generatrix of a cylinder, a limiting case of a cone, is a line that is kept parallel to some axis. See also * Surface of revolution A surface of revolution is a surface in Euclidean space created by rotating a curve (the generatrix) around an axis of rotation. Examples of surfaces of revolution generated by a straight line are cylindrical and conical surfaces depending on ... References Elementary geometry Computer graphics { ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line (geometry), line, but that does not have to be Linearity, straight. Intuitively, a curve may be thought of as the trace left by a moving point (geometry), point. This is the definition that appeared more than 2000 years ago in Euclid's Elements, Euclid's ''Elements'': "The [curved] line is […] the first species of quantity, which has only one dimension, namely length, without any width nor depth, and is nothing else than the flow or run of the point which […] will leave from its imaginary moving some vestige in length, exempt of any width." This definition of a curve has been formalized in modern mathematics as: ''A curve is the image (mathematics), image of an interval (mathematics), interval to a topological space by a continuous function''. In some contexts, the function that defines the curve is called a ''parametrization'', and the curve is a parametric curve. In this artic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |