|
Perspectivity
In geometry and in its applications to drawing, a perspectivity is the formation of an image in a picture plane of a scene viewed from a fixed point. Graphics The science of graphical perspective uses perspectivities to make realistic images in proper proportion. According to Kirsti Andersen, the first author to describe perspectivity was Leon Alberti in his ''De Pictura'' (1435). In English, Brook Taylor presented his ''Linear Perspective'' in 1715, where he explained "Perspective is the Art of drawing on a Plane the Appearances of any Figures, by the Rules of Geometry". In a second book, ''New Principles of Linear Perspective'' (1719), Taylor wrote :When Lines drawn according to a certain Law from the several Parts of any Figure, cut a Plane, and by that Cutting or Intersection describe a figure on that Plane, that Figure so described is called the ''Projection'' of the other Figure. The Lines producing that Projection, taken all together, are called the ''System of Rays''. And ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Desargues's Theorem
In projective geometry, Desargues's theorem, named after Girard Desargues, states: :Two triangles are in perspective ''axially'' if and only if they are in perspective ''centrally''. Denote the three vertices of one triangle by and , and those of the other by and . ''Axial perspectivity'' means that lines and meet in a point, lines and meet in a second point, and lines and meet in a third point, and that these three points all lie on a common line called the ''axis of perspectivity''. ''Central perspectivity'' means that the three lines and are concurrent, at a point called the ''center of perspectivity''. This intersection theorem is true in the usual Euclidean plane but special care needs to be taken in exceptional cases, as when a pair of sides are parallel, so that their "point of intersection" recedes to infinity. Commonly, to remove these exceptions, mathematicians "complete" the Euclidean plane by adding points at infinity, following Jean-Victor Poncelet. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
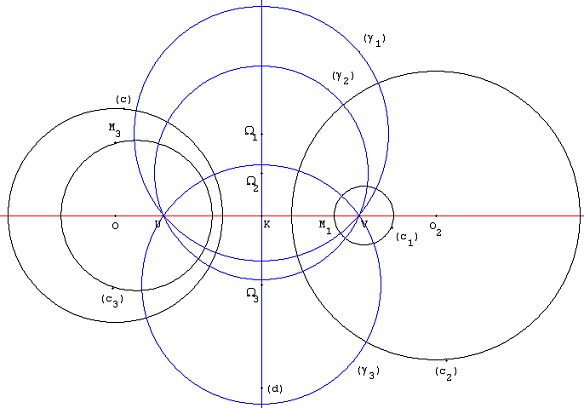
Perspective (geometry)
Two figures in a plane are perspective from a point ''O'', called the center of perspectivity if the lines joining corresponding points of the figures all meet at ''O''. Dually, the figures are said to be perspective from a line if the points of intersection of corresponding lines all lie on one line. The proper setting for this concept is in projective geometry where there will be no special cases due to parallel lines since all lines meet. Although stated here for figures in a plane, the concept is easily extended to higher dimensions. Terminology The line which goes through the points where the figure's corresponding sides intersect is known as the axis of perspectivity, perspective axis, homology axis, or archaically, perspectrix. The figures are said to be perspective from this axis. The point at which the lines joining the corresponding vertices of the perspective figures intersect is called the center of perspectivity, perspective center, homology center, pole, or archaica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homography
In projective geometry, a homography is an isomorphism of projective spaces, induced by an isomorphism of the vector spaces from which the projective spaces derive. It is a bijection that maps lines to lines, and thus a collineation. In general, some collineations are not homographies, but the fundamental theorem of projective geometry asserts that is not so in the case of real projective spaces of dimension at least two. Synonyms include projectivity, projective transformation, and projective collineation. Historically, homographies (and projective spaces) have been introduced to study perspective and projections in Euclidean geometry, and the term ''homography'', which, etymologically, roughly means "similar drawing", dates from this time. At the end of the 19th century, formal definitions of projective spaces were introduced, which differed from extending Euclidean or affine spaces by adding points at infinity. The term "projective transformation" originated in these abstra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts. The basic intuitions are that projective space has more points than Euclidean space, for a given dimension, and that geometric transformations are permitted that transform the extra points (called "points at infinity") to Euclidean points, and vice-versa. Properties meaningful for projective geometry are respected by this new idea of transformation, which is more radical in its effects than can be expressed by a transformation matrix and translations (the affine transformations). The first issue for geometers is what kind of geometry is adequate for a novel situation. It is not possible to refer to angles in projective geometry as it is in Euclidean geometry, because angle is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts. The basic intuitions are that projective space has more points than Euclidean space, for a given dimension, and that geometric transformations are permitted that transform the extra points (called "points at infinity") to Euclidean points, and vice-versa. Properties meaningful for projective geometry are respected by this new idea of transformation, which is more radical in its effects than can be expressed by a transformation matrix and translations (the affine transformations). The first issue for geometers is what kind of geometry is adequate for a novel situation. It is not possible to refer to angles in projective geometry as it is in Euclidean geometry, because angle is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Duality (projective Geometry)
In geometry, a striking feature of projective planes is the symmetry of the roles played by points and lines in the definitions and theorems, and (plane) duality is the formalization of this concept. There are two approaches to the subject of duality, one through language () and the other a more functional approach through special mappings. These are completely equivalent and either treatment has as its starting point the axiomatic version of the geometries under consideration. In the functional approach there is a map between related geometries that is called a ''duality''. Such a map can be constructed in many ways. The concept of plane duality readily extends to space duality and beyond that to duality in any finite-dimensional projective geometry. Principle of duality A projective plane may be defined axiomatically as an incidence structure, in terms of a set of ''points'', a set of ''lines'', and an incidence relation that determines which points lie on which lines. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Technical Drawing
Technical drawing, drafting or drawing, is the act and Academic discipline, discipline of composing Plan (drawing), drawings that Visual communication, visually communicate how something functions or is constructed. Technical drawing is essential for communicating ideas in Manufacturing, industry and engineering. To make the drawings easier to understand, people use familiar symbols, Perspective (graphical), perspectives, units of measurement, notation systems, visual styles, and page layout. Together, such Convention (norm), conventions constitute a visual language and help to ensure that the drawing is unambiguous and relatively easy to understand. Many of the symbols and principles of technical drawing are codified in an international standard called ISO 128. The need for precise communication in the preparation of a functional document distinguishes technical drawing from the expressive drawing of the visual arts. Artistic drawings are subjectively interpreted; their meanin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
University Of Brighton
The University of Brighton is a public university based on four campuses in Brighton and Eastbourne on the south coast of England. Its roots can be traced back to 1858 when the Brighton School of Art was opened in the Royal Pavilion. It achieved university status in 1992. The University focuses on professional education, with the majority of degrees awarded also recognised by professional organisations or leading to professional qualifications. Subjects include pharmacy, engineering, ecology, computing, mathematics, architecture, geology, nursing, teaching, sport science, journalism, criminology and business. It has around 18,000 students and 2,400 staff. History In 1858 the Brighton School of Art opened its doors to its first 110 students, in rooms by the kitchens of the Royal Pavilion. It moved in 1876 to its own building in Grand Parade, with the Prime Minister, William Gladstone, witnessing the laying of the new building's foundation stone. The Municipal School of Scien ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rice University
William Marsh Rice University (Rice University) is a Private university, private research university in Houston, Houston, Texas. It is on a 300-acre campus near the Houston Museum District and adjacent to the Texas Medical Center. Rice is ranked among the top universities in the United States. Opened in 1912 as the Rice Institute after the murder of its namesake William Marsh Rice, Rice is a research university with an undergraduate focus. Its emphasis on undergraduate education is demonstrated by its 6:1 student-faculty ratio. The university has a Research I university, very high level of research activity, with $156 million in sponsored research funding in 2019. Rice is noted for its applied science programs in the fields of artificial heart research, structural chemical analysis, signal processing, space science, and nanotechnology. Rice has been a member of the Association of American Universities since 1985 and is Carnegie Classification of Institutions of Higher Education ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Wiley & Sons
John Wiley & Sons, Inc., commonly known as Wiley (), is an American multinational publishing company founded in 1807 that focuses on academic publishing and instructional materials. The company produces books, journals, and encyclopedias, in print and electronically, as well as online products and services, training materials, and educational materials for undergraduate, graduate, and continuing education students. History The company was established in 1807 when Charles Wiley opened a print shop in Manhattan. The company was the publisher of 19th century American literary figures like James Fenimore Cooper, Washington Irving, Herman Melville, and Edgar Allan Poe, as well as of legal, religious, and other non-fiction titles. The firm took its current name in 1865. Wiley later shifted its focus to scientific, technical, and engineering subject areas, abandoning its literary interests. Wiley's son John (born in Flatbush, New York, October 4, 1808; died in East Orange, New Je ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Breuil - Diverses Methodes Universelles Et Nouvelles, En Tout Ou En Partie Pour Faire Des Perspectives, 1642 - 177384
Breuil may refer to the following: People * Beta Breuil (1876 – after 1918), American script editor and screenwriter * Henri Breuil (1877–1961), French archeologist and ethnographer * Alphonse du Breuil (1811–1885), French botanist * Christophe Breuil (born 1968), French mathematician Places France * Breuil, Somme, in the Somme ''département'' *Breuil-Barret, in the Vendée ''département'' *Breuil-Bois-Robert, in the Yvelines ''département'' *Breuil-la-Réorte, in the Charente-Maritime ''département'' * Breuil-le-Sec, in the Oise ''département'' * Breuil-le-Vert, in the Oise ''département'' *Breuil-Magné, in the Charente-Maritime ''département'' *Breuil-sur-Vesle, in the Marne ''département'' Italy *Breuil-Cervinia Breuil-Cervinia (french: Breuil; it, Cervinia; Valdôtain: ) is a ''frazione'' of the ''comune'' of Valtournenche, and is considered one of the most renowned winter and summer tourist resorts in the Alps. Etymology The name of ''Breuil-Cervi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perspective Projection
Linear or point-projection perspective (from la, perspicere 'to see through') is one of two types of graphical projection perspective in the graphic arts; the other is parallel projection. Linear perspective is an approximate representation, generally on a flat surface, of an image as it is seen by the eye. Perspective drawing is useful for representing a three-dimensional scene in a two-dimensional medium, like paper. The most characteristic features of linear perspective are that objects appear smaller as their distance from the observer increases, and that they are subject to ''foreshortening'', meaning that an object's dimensions along the line of sight appear shorter than its dimensions across the line of sight. All objects will recede to points in the distance, usually along the horizon line, but also above and below the horizon line depending on the view used. Italian Renaissance painters and architects including Masaccio, Paolo Uccello, Piero della Francesca and Luca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
