|
Partition Algebra
The partition algebra is an associative algebra with a basis of partition of a set, set-partition diagrams and multiplication given by diagram Path (topology)#Path composition, concatenation. Its subalgebras include diagram algebras such as the Brauer algebra, the Temperley-Lieb algebra, Temperley–Lieb algebra, or the group ring, group algebra of the symmetric group. Representations of the partition algebra are built from sets of diagrams and from representations of the symmetric group. Definition Diagrams A partition of 2k elements labelled 1,\bar 1, 2,\bar 2,\dots, k,\bar k is represented as a diagram, with lines connecting elements in the same subset. In the following example, the subset \ gives rise to the lines \bar 1 - \bar 4, \bar 4 -\bar 5, \bar 5 - 6, and could equivalently be represented by the lines \bar 1- 6, \bar 4 - 6, \bar 5 - 6, \bar 1 - \bar 5 (for instance). For n\in \mathbb and k\in \mathbb^*, the partition algebra P_k(n) is defined by a \mathbb-basis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Associative Algebra
In mathematics, an associative algebra ''A'' over a commutative ring (often a field) ''K'' is a ring ''A'' together with a ring homomorphism from ''K'' into the center of ''A''. This is thus an algebraic structure with an addition, a multiplication, and a scalar multiplication (the multiplication by the image of the ring homomorphism of an element of ''K''). The addition and multiplication operations together give ''A'' the structure of a ring; the addition and scalar multiplication operations together give ''A'' the structure of a module or vector space over ''K''. In this article we will also use the term ''K''-algebra to mean an associative algebra over ''K''. A standard first example of a ''K''-algebra is a ring of square matrices over a commutative ring ''K'', with the usual matrix multiplication. A commutative algebra is an associative algebra for which the multiplication is commutative, or, equivalently, an associative algebra that is also a commutative ring. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
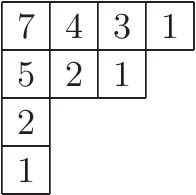
Partition Ex M
Partition may refer to: Arts and entertainment Film and television * ''Partition'' (1987 film), directed by Ken McMullen * ''Partition'' (2007 film), directed by Vic Sarin * '' Partition: 1947'', or ''Viceroy's House'', a 2017 film Music * Partition (music), a segment created from a set * "Partition" (song), by Beyoncé, 2014 * ''Partition'', soundtrack to the 2007 film by Brian Tyler Law and politics * Partition (law), the division of an estate * Partition (politics), a change of political borders, including: ** Partition of India ** Partition of Ireland ** Partitions of Poland Science and technology Computing * Disk partitioning, the division of a hard disk drive * Memory partition, a memory management technique * Partition (database), the division of a logical database * Logical partition, a subset of a computer's resources, virtualized as a separate computer * Binary space partitioning, in computer science * Partition problem, in number theory and computer science Math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Young Tableaux
In mathematics, a Young tableau (; plural: tableaux) is a combinatorial object useful in representation theory and Schubert calculus. It provides a convenient way to describe the group representations of the symmetric and general linear groups and to study their properties. Young tableaux were introduced by Alfred Young, a mathematician at Cambridge University, in 1900. They were then applied to the study of the symmetric group by Georg Frobenius in 1903. Their theory was further developed by many mathematicians, including Percy MacMahon, W. V. D. Hodge, G. de B. Robinson, Gian-Carlo Rota, Alain Lascoux, Marcel-Paul Schützenberger and Richard P. Stanley. Definitions ''Note: this article uses the English convention for displaying Young diagrams and tableaux''. Diagrams A Young diagram (also called a Ferrers diagram, particularly when represented using dots) is a finite collection of boxes, or cells, arranged in left-justified rows, with the row lengths in non-i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hook Length Formula
In combinatorics, combinatorial mathematics, the hook length formula is a formula for the number of Young tableau, standard Young tableaux whose shape is a given Young diagram. It has applications in diverse areas of mathematics, areas such as representation theory, probability theory, probability, and algorithm analysis; for example, the problem of longest increasing subsequences. A related formula gives the number of semi-standard Young tableaux, which is a specialization of a Schur polynomial. Definitions and statement Let \lambda=(\lambda_1\geq \cdots\geq \lambda_k) be a integer partition, partition of n=\lambda_1+\cdots+\lambda_k. It is customary to interpret \lambda graphically as a Young diagram, namely a left-justified array of square cells with k rows of lengths \lambda_1,\ldots,\lambda_k. A (standard) Young tableau of shape \lambda is a filling of the n cells of the Young diagram with all the integers \, with no repetition, such that each row and each column form incre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Binomial Coefficient
In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers and is written \tbinom. It is the coefficient of the term in the polynomial expansion of the binomial power ; this coefficient can be computed by the multiplicative formula : \binom nk = \frac, which using factorial notation can be compactly expressed as : \binom = \frac. For example, the fourth power of is : \begin (1 + x)^4 &= \tbinom x^0 + \tbinom x^1 + \tbinom x^2 + \tbinom x^3 + \tbinom x^4 \\ &= 1 + 4x + 6 x^2 + 4x^3 + x^4, \end and the binomial coefficient \tbinom =\tfrac = \tfrac = 6 is the coefficient of the term. Arranging the numbers \tbinom, \tbinom, \ldots, \tbinom in successive rows for gives a triangular array called Pascal's triangle, satisfying the recurrence relation : \binom = \binom + \binom . The binomial coefficients occur in many areas of mathematics, and espe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Stirling Number Of The Second Kind
In mathematics, particularly in combinatorics, a Stirling number of the second kind (or Stirling partition number) is the number of ways to partition a set of ''n'' objects into ''k'' non-empty subsets and is denoted by S(n,k) or \textstyle \left\. Stirling numbers of the second kind occur in the field of mathematics called combinatorics and the study of partitions. They are named after James Stirling. The Stirling numbers of the first and second kind can be understood as inverses of one another when viewed as triangular matrices. This article is devoted to specifics of Stirling numbers of the second kind. Identities linking the two kinds appear in the article on Stirling numbers. Definition The Stirling numbers of the second kind, written S(n,k) or \lbrace\textstyle\rbrace or with other notations, count the number of ways to partition a set of n labelled objects into k nonempty unlabelled subsets. Equivalently, they count the number of different equivalence relations with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Specht Module
In mathematics, a Specht module is one of the representations of symmetric groups studied by . They are indexed by partitions, and in characteristic 0 the Specht modules of partitions of ''n'' form a complete set of irreducible representations of the symmetric group on ''n'' points. Definition Fix a partition λ of ''n'' and a commutative ring ''k''. The partition determines a Young diagram with ''n'' boxes. A Young tableau of shape λ is a way of labelling the boxes of this Young diagram by distinct numbers 1, \dots, n. A tabloid is an equivalence class of Young tableaux where two labellings are equivalent if one is obtained from the other by permuting the entries of each row. For each Young tableau ''T'' of shape λ let \ be the corresponding tabloid. The symmetric group on ''n'' points acts on the set of Young tableaux of shape λ. Consequently, it acts on tabloids, and on the free ''k''-module ''V'' with the tabloids as basis. Given a Young table ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Partition Representation
Partition may refer to: Arts and entertainment Film and television * ''Partition'' (1987 film), directed by Ken McMullen * ''Partition'' (2007 film), directed by Vic Sarin * '' Partition: 1947'', or ''Viceroy's House'', a 2017 film Music * Partition (music), a segment created from a set * "Partition" (song), by Beyoncé, 2014 * ''Partition'', soundtrack to the 2007 film by Brian Tyler Law and politics * Partition (law), the division of an estate * Partition (politics), a change of political borders, including: ** Partition of India ** Partition of Ireland ** Partitions of Poland Science and technology Computing * Disk partitioning, the division of a hard disk drive * Memory partition, a memory management technique * Partition (database), the division of a logical database * Logical partition, a subset of a computer's resources, virtualized as a separate computer * Binary space partitioning, in computer science * Partition problem, in number theory and computer science Mathe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Symmetric Group
In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric group \mathrm_n defined over a finite set of n symbols consists of the permutations that can be performed on the n symbols. Since there are n! (n factorial) such permutation operations, the order (number of elements) of the symmetric group \mathrm_n is n!. Although symmetric groups can be defined on infinite sets, this article focuses on the finite symmetric groups: their applications, their elements, their conjugacy classes, a finite presentation, their subgroups, their automorphism groups, and their representation theory. For the remainder of this article, "symmetric group" will mean a symmetric group on a finite set. The symmetric group is important to diverse areas of mathematics such as Galois theory, invariant theory, the re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Partition Ex PR
Partition may refer to: Arts and entertainment Film and television * ''Partition'' (1987 film), directed by Ken McMullen * ''Partition'' (2007 film), directed by Vic Sarin * '' Partition: 1947'', or ''Viceroy's House'', a 2017 film Music * Partition (music), a segment created from a set * "Partition" (song), by Beyoncé, 2014 * ''Partition'', soundtrack to the 2007 film by Brian Tyler Law and politics * Partition (law), the division of an estate * Partition (politics), a change of political borders, including: ** Partition of India ** Partition of Ireland ** Partitions of Poland Science and technology Computing * Disk partitioning, the division of a hard disk drive * Memory partition, a memory management technique * Partition (database), the division of a logical database * Logical partition, a subset of a computer's resources, virtualized as a separate computer * Binary space partitioning, in computer science * Partition problem, in number theory and computer science Mathe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |