|
Proximal Gradient Methods For Learning
Proximal gradient (forward backward splitting) methods for learning is an area of research in optimization and statistical learning theory which studies algorithms for a general class of Convex function#Definition, convex Regularization (mathematics), regularization problems where the regularization penalty may not be Differentiable function, differentiable. One such example is \ell_1 regularization (also known as Lasso) of the form :\min_ \frac\sum_^n (y_i- \langle w,x_i\rangle)^2+ \lambda \, w\, _1, \quad \text x_i\in \mathbb^d\text y_i\in\mathbb. Proximal gradient methods offer a general framework for solving regularization problems from statistical learning theory with penalties that are tailored to a specific problem application. Such customized penalties can help to induce certain structure in problem solutions, such as ''sparsity'' (in the case of Lasso (statistics), lasso) or ''group structure'' (in the case of Lasso (statistics)#Group LASSO, group lasso). Relevant backgro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries. In the more general approach, an optimization problem consists of maxima and minima, maximizing or minimizing a Function of a real variable, real function by systematically choosing Argument of a function, input values from within an allowed set and computing the Value (mathematics), value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. Optimization problems Opti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Space
In mathematics and physics, a vector space (also called a linear space) is a set (mathematics), set whose elements, often called vector (mathematics and physics), ''vectors'', can be added together and multiplied ("scaled") by numbers called scalar (mathematics), ''scalars''. The operations of vector addition and scalar multiplication must satisfy certain requirements, called ''vector axioms''. Real vector spaces and complex vector spaces are kinds of vector spaces based on different kinds of scalars: real numbers and complex numbers. Scalars can also be, more generally, elements of any field (mathematics), field. Vector spaces generalize Euclidean vectors, which allow modeling of Physical quantity, physical quantities (such as forces and velocity) that have not only a Magnitude (mathematics), magnitude, but also a Orientation (geometry), direction. The concept of vector spaces is fundamental for linear algebra, together with the concept of matrix (mathematics), matrices, which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Learning Theory
Statistical learning theory is a framework for machine learning drawing from the fields of statistics and functional analysis. Statistical learning theory deals with the statistical inference problem of finding a predictive function based on data. Statistical learning theory has led to successful applications in fields such as computer vision, speech recognition, and bioinformatics. Introduction The goals of learning are understanding and prediction. Learning falls into many categories, including supervised learning, unsupervised learning, online learning, and reinforcement learning. From the perspective of statistical learning theory, supervised learning is best understood. Supervised learning involves learning from a training set of data. Every point in the training is an input–output pair, where the input maps to an output. The learning problem consists of inferring the function that maps between the input and the output, such that the learned function can be used to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Analysis
Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex optimization, convex minimization, a subdomain of optimization (mathematics), optimization theory. Convex sets A subset C \subseteq X of some vector space X is if it satisfies any of the following equivalent conditions: #If 0 \leq r \leq 1 is real and x, y \in C then r x + (1 - r) y \in C. #If 0 < r < 1 is real and with then Throughout, will be a map valued in the Extended real number line, extended real numbers with a Domain of a function, domain that is a convex subset of some vector space. The map is a if holds for any real and any |
Directed Acyclic Graph
In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG) is a directed graph with no directed cycles. That is, it consists of vertices and edges (also called ''arcs''), with each edge directed from one vertex to another, such that following those directions will never form a closed loop. A directed graph is a DAG if and only if it can be topologically ordered, by arranging the vertices as a linear ordering that is consistent with all edge directions. DAGs have numerous scientific and computational applications, ranging from biology (evolution, family trees, epidemiology) to information science (citation networks) to computation (scheduling). Directed acyclic graphs are also called acyclic directed graphs or acyclic digraphs. Definitions A graph is formed by vertices and by edges connecting pairs of vertices, where the vertices can be any kind of object that is connected in pairs by edges. In the case of a directed graph, each edg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Norm
In functional analysis, the dual norm is a measure of size for a continuous function, continuous linear function defined on a normed vector space. Definition Let X be a normed vector space with norm \, \cdot\, and let X^* denote its continuous dual space. The dual norm of a continuous linear functional f belonging to X^* is the non-negative real number defined by any of the following equivalent formulas: \begin \, f \, &= \sup &&\ \\ &= \sup &&\ \\ &= \inf &&\ \\ &= \sup &&\ \\ &= \sup &&\ \;\;\;\text X \neq \ \\ &= \sup &&\bigg\ \;\;\;\text X \neq \ \\ \end where \sup and \inf denote the supremum and infimum, respectively. The constant 0 map is the origin of the vector space X^* and it always has norm \, 0\, = 0. If X = \ then the only linear functional on X is the constant 0 map and moreover, the sets in the last two rows will both be empty and consequently, their supremums will equal \sup \varnothing = - \infty instead of the corre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ball (mathematics)
In mathematics, a ball is the solid figure bounded by a ''sphere''; it is also called a solid sphere. It may be a closed ball (including the boundary points that constitute the sphere) or an open ball (excluding them). These concepts are defined not only in three-dimensional Euclidean space but also for lower and higher dimensions, and for metric spaces in general. A ''ball'' in dimensions is called a hyperball or -ball and is bounded by a ''hypersphere'' or ()-sphere. Thus, for example, a ball in the Euclidean plane is the same thing as a disk, the planar region bounded by a circle. In Euclidean 3-space, a ball is taken to be the region of space bounded by a 2-dimensional sphere. In a one-dimensional space, a ball is a line segment. In other contexts, such as in Euclidean geometry and informal use, ''sphere'' is sometimes used to mean ''ball''. In the field of topology the closed n-dimensional ball is often denoted as B^n or D^n while the open n-dimensional ball is \o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moreau Decomposition
Moreau may refer to: People *Moreau (surname) Places *Moreau, New York * Moreau River (other) Music *An alternate name for the band Cousteau, used for the album ''Nova Scotia'' in the United States for legal reasons In fiction *Dr. Moreau, the anti villain of '' The Island of Dr. Moreau'', an 1896 science fiction novel by H. G. Wells, and various film adaptations *Andre-Louis Moreau, the hero of ''Scaramouche'', a historical novel by Rafael Sabatini. *Moreau series of novels by S. Andrew Swann *Jeff "Joker" Moreau, flight lieutenant in the video game ''Mass Effect'' *Moreau, half-human-half-animal race in the role-playing game ''D20 Modern ''d20 Modern'' is a modern fantasy role-playing game system designed by Bill Slavicsek, Jeff Grubb, Rich Redman, and Charles Ryan. The system's core rulebook was published by Wizards of the Coast on November 1, 2002; by 2006, ten additional supp ...'' *Damien Moreau, villain in season 3 of the television show '' Leverage'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elastic Net Regularization
In statistics and, in particular, in the fitting of linear or logistic regression models, the elastic net is a regularized regression method that linearly combines the ''L''1 and ''L''2 penalties of the lasso and ridge methods. Nevertheless, elastic net regularization is typically more accurate than both methods with regard to reconstruction. Specification The elastic net method overcomes the limitations of the LASSO (least absolute shrinkage and selection operator) method which uses a penalty function based on :\, \beta\, _1 = \textstyle \sum_^p , \beta_j, . Use of this penalty function has several limitations. For example, in the "large ''p'', small ''n''" case (high-dimensional data with few examples), the LASSO selects at most ''n'' variables before it saturates. Also if there is a group of highly correlated variables, then the LASSO tends to select one variable from a group and ignore the others. To overcome these limitations, the elastic net adds a quadratic part (\, \bet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rate Of Convergence
In mathematical analysis, particularly numerical analysis, the rate of convergence and order of convergence of a sequence that converges to a limit are any of several characterizations of how quickly that sequence approaches its limit. These are broadly divided into rates and orders of convergence that describe how quickly a sequence further approaches its limit once it is already close to it, called asymptotic rates and orders of convergence, and those that describe how quickly sequences approach their limits from starting points that are not necessarily close to their limits, called non-asymptotic rates and orders of convergence. Asymptotic behavior is particularly useful for deciding when to stop a sequence of numerical computations, for instance once a target precision has been reached with an iterative root-finding algorithm, but pre-asymptotic behavior is often crucial for determining whether to begin a sequence of computations at all, since it may be impossible or imprac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gradient Descent
Gradient descent is a method for unconstrained mathematical optimization. It is a first-order iterative algorithm for minimizing a differentiable multivariate function. The idea is to take repeated steps in the opposite direction of the gradient (or approximate gradient) of the function at the current point, because this is the direction of steepest descent. Conversely, stepping in the direction of the gradient will lead to a trajectory that maximizes that function; the procedure is then known as ''gradient ascent''. It is particularly useful in machine learning for minimizing the cost or loss function. Gradient descent should not be confused with local search algorithms, although both are iterative methods for optimization. Gradient descent is generally attributed to Augustin-Louis Cauchy, who first suggested it in 1847. Jacques Hadamard independently proposed a similar method in 1907. Its convergence properties for non-linear optimization problems were first studied by Has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
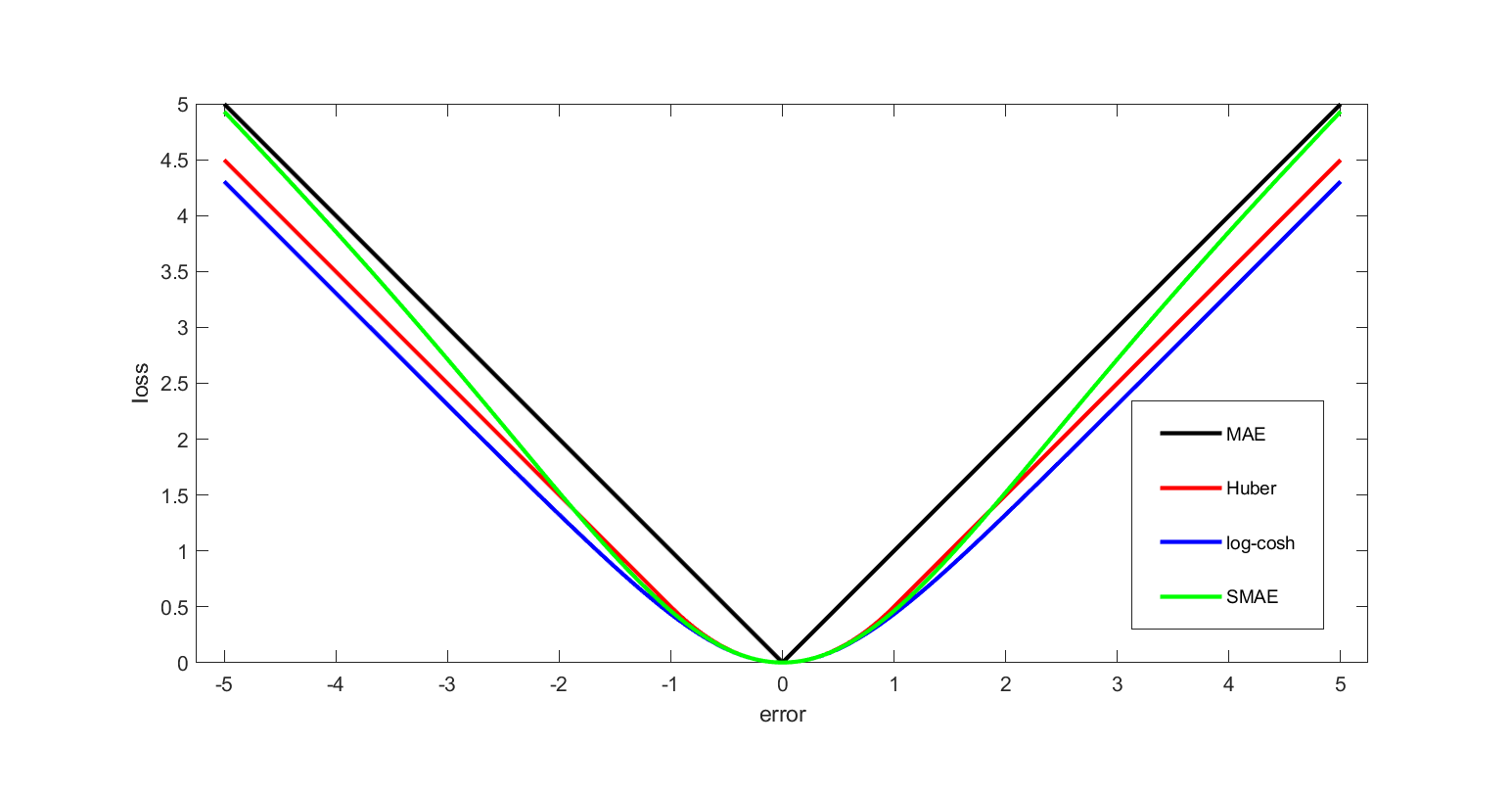
Loss Function
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite (in specific domains, variously called a reward function, a profit function, a utility function, a fitness function, etc.), in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy. In statistics, typically a loss function is used for parameter estimation, and the event in question is some function of the difference between estimated and true values for an instance of data. The concept, as old as Pierre-Simon Laplace, Laplace, was reintroduced in statistics by Abraham Wald in the middle of the 20th century. In the context of economi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |