|
Projector (linear Algebra)
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself (an endomorphism) such that P\circ P=P. That is, whenever P is applied twice to any vector, it gives the same result as if it were applied once (i.e. P is idempotent). It leaves its image unchanged. This definition of "projection" formalizes and generalizes the idea of graphical projection. One can also consider the effect of a projection on a geometrical object by examining the effect of the projection on points in the object. Definitions A projection on a vector space V is a linear operator P : V \to V such that P^2 = P. When V has an inner product and is complete (i.e. when V is a Hilbert space) the concept of orthogonality can be used. A projection P on a Hilbert space V is called an orthogonal projection if it satisfies \langle P \mathbf x, \mathbf y \rangle = \langle \mathbf x, P \mathbf y \rangle for all \mathbf x, \mathbf y \in V. A projection on a Hilber ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonal Projection
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself (an endomorphism) such that P\circ P=P. That is, whenever P is applied twice to any vector, it gives the same result as if it were applied once (i.e. P is idempotent). It leaves its image unchanged. This definition of "projection" formalizes and generalizes the idea of graphical projection. One can also consider the effect of a projection on a geometrical object by examining the effect of the projection on points in the object. Definitions A projection on a vector space V is a linear operator P : V \to V such that P^2 = P. When V has an inner product and is complete (i.e. when V is a Hilbert space) the concept of orthogonality can be used. A projection P on a Hilbert space V is called an orthogonal projection if it satisfies \langle P \mathbf x, \mathbf y \rangle = \langle \mathbf x, P \mathbf y \rangle for all \mathbf x, \mathbf y \in V. A projection ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix (mathematics)
In mathematics, a matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two by three matrix", a "-matrix", or a matrix of dimension . Without further specifications, matrices represent linear maps, and allow explicit computations in linear algebra. Therefore, the study of matrices is a large part of linear algebra, and most properties and operations of abstract linear algebra can be expressed in terms of matrices. For example, matrix multiplication represents composition of linear maps. Not all matrices are related to linear algebra. This is, in particular, the case in graph theory, of incidence matrices, and adjacency matrices. ''This article focuses on matrices related to linear algebra, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Subspace
In mathematics, and more specifically in linear algebra, a linear subspace, also known as a vector subspaceThe term ''linear subspace'' is sometimes used for referring to flats and affine subspaces. In the case of vector spaces over the reals, linear subspaces, flats, and affine subspaces are also called ''linear manifolds'' for emphasizing that there are also manifolds. is a vector space that is a subset of some larger vector space. A linear subspace is usually simply called a ''subspace'' when the context serves to distinguish it from other types of subspaces. Definition If ''V'' is a vector space over a field ''K'' and if ''W'' is a subset of ''V'', then ''W'' is a linear subspace of ''V'' if under the operations of ''V'', ''W'' is a vector space over ''K''. Equivalently, a nonempty subset ''W'' is a subspace of ''V'' if, whenever are elements of ''W'' and are elements of ''K'', it follows that is in ''W''. As a corollary, all vector spaces are equipped with at least ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subspace Topology
In topology and related areas of mathematics, a subspace of a topological space ''X'' is a subset ''S'' of ''X'' which is equipped with a topology induced from that of ''X'' called the subspace topology (or the relative topology, or the induced topology, or the trace topology). Definition Given a topological space (X, \tau) and a subset S of X, the subspace topology on S is defined by :\tau_S = \lbrace S \cap U \mid U \in \tau \rbrace. That is, a subset of S is open in the subspace topology if and only if it is the intersection of S with an open set in (X, \tau). If S is equipped with the subspace topology then it is a topological space in its own right, and is called a subspace of (X, \tau). Subsets of topological spaces are usually assumed to be equipped with the subspace topology unless otherwise stated. Alternatively we can define the subspace topology for a subset S of X as the coarsest topology for which the inclusion map :\iota: S \hookrightarrow X is continuous. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Domain Of A Function
In mathematics, the domain of a function is the set of inputs accepted by the function. It is sometimes denoted by \operatorname(f) or \operatornamef, where is the function. More precisely, given a function f\colon X\to Y, the domain of is . Note that in modern mathematical language, the domain is part of the definition of a function rather than a property of it. In the special case that and are both subsets of \R, the function can be graphed in the Cartesian coordinate system. In this case, the domain is represented on the -axis of the graph, as the projection of the graph of the function onto the -axis. For a function f\colon X\to Y, the set is called the codomain, and the set of values attained by the function (which is a subset of ) is called its range or image. Any function can be restricted to a subset of its domain. The restriction of f \colon X \to Y to A, where A\subseteq X, is written as \left. f \_A \colon A \to Y. Natural domain If a real function is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Open Set
In mathematics, open sets are a generalization of open intervals in the real line. In a metric space (a set along with a distance defined between any two points), open sets are the sets that, with every point , contain all points that are sufficiently near to (that is, all points whose distance to is less than some value depending on ). More generally, one defines open sets as the members of a given collection of subsets of a given set, a collection that has the property of containing every union of its members, every finite intersection of its members, the empty set, and the whole set itself. A set in which such a collection is given is called a topological space, and the collection is called a topology. These conditions are very loose, and allow enormous flexibility in the choice of open sets. For example, ''every'' subset can be open (the discrete topology), or no set can be open except the space itself and the empty set (the indiscrete topology). In practice ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Open Map
In mathematics, more specifically in topology, an open map is a function between two topological spaces that maps open sets to open sets. That is, a function f : X \to Y is open if for any open set U in X, the image f(U) is open in Y. Likewise, a closed map is a function that maps closed sets to closed sets. A map may be open, closed, both, or neither; in particular, an open map need not be closed and vice versa. Open and closed maps are not necessarily continuous. Further, continuity is independent of openness and closedness in the general case and a continuous function may have one, both, or neither property; this fact remains true even if one restricts oneself to metric spaces. Although their definitions seem more natural, open and closed maps are much less important than continuous maps. Recall that, by definition, a function f : X \to Y is continuous if the preimage of every open set of Y is open in X. (Equivalently, if the preimage of every closed set of Y is closed in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
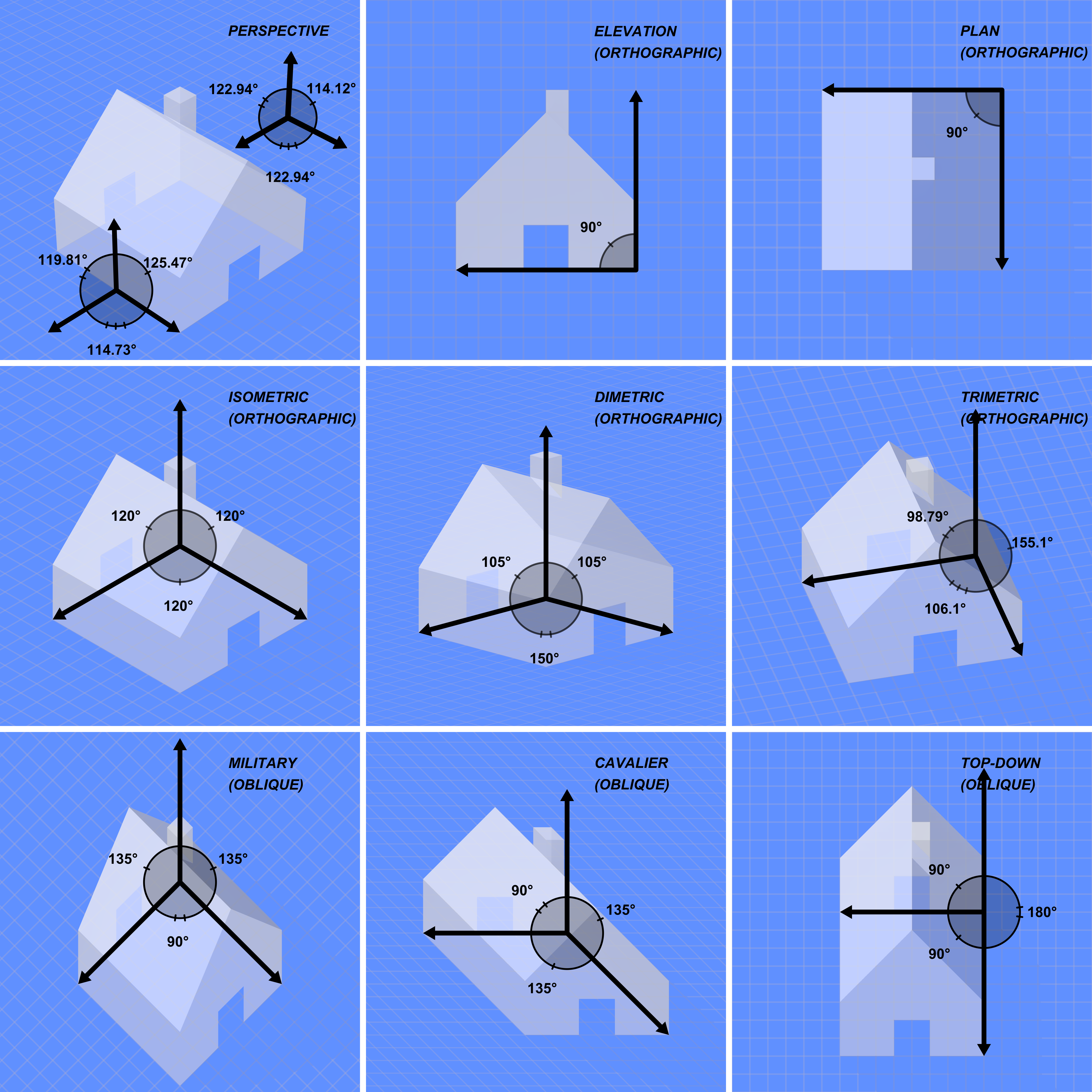
Oblique Projection
Oblique projection is a simple type of technical drawing of graphical projection used for producing two-dimensional (2D) images of three-dimensional (3D) objects. The objects are not in perspective and so do not correspond to any view of an object that can be obtained in practice, but the technique yields somewhat convincing and useful. Oblique projection is commonly used in technical drawing. The cavalier projection was used by French military artists in the 18th century to depict fortifications. Oblique projection was used almost universally by Chinese artists from the 1st or 2nd centuries to the 18th century, especially to depict rectilinear objects such as houses. Various graphical projection techniques can be used in computer graphics, including in Computer Aided Design (CAD), computer games, computer generated animations, and special effects used in movies. Overview Oblique projection is a type of parallel projection: * it projects an image by intersecting pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
If And Only If
In logic and related fields such as mathematics and philosophy, "if and only if" (shortened as "iff") is a biconditional logical connective between statements, where either both statements are true or both are false. The connective is biconditional (a statement of material equivalence), and can be likened to the standard material conditional ("only if", equal to "if ... then") combined with its reverse ("if"); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. For example, ''P if and only if Q'' means that ''P'' is true whenever ''Q'' is true, and the only case in which ''P'' is true is if ''Q'' is also true, whereas in the case of ''P if Q'', there could be other scenarios where ''P'' is true and ''Q' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Multiplication
In mathematics, particularly in linear algebra, matrix multiplication is a binary operation that produces a matrix from two matrices. For matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix. The resulting matrix, known as the matrix product, has the number of rows of the first and the number of columns of the second matrix. The product of matrices and is denoted as . Matrix multiplication was first described by the French mathematician Jacques Philippe Marie Binet in 1812, to represent the composition of linear maps that are represented by matrices. Matrix multiplication is thus a basic tool of linear algebra, and as such has numerous applications in many areas of mathematics, as well as in applied mathematics, statistics, physics, economics, and engineering. Computing matrix products is a central operation in all computational applications of linear algebra. Notation This article will use the following n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Vector
In mathematics, physics, and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector or spatial vector) is a geometric object that has magnitude (or length) and direction. Vectors can be added to other vectors according to vector algebra. A Euclidean vector is frequently represented by a ''directed line segment'', or graphically as an arrow connecting an ''initial point'' ''A'' with a ''terminal point'' ''B'', and denoted by \overrightarrow . A vector is what is needed to "carry" the point ''A'' to the point ''B''; the Latin word ''vector'' means "carrier". It was first used by 18th century astronomers investigating planetary revolution around the Sun. The magnitude of the vector is the distance between the two points, and the direction refers to the direction of displacement from ''A'' to ''B''. Many algebraic operations on real numbers such as addition, subtraction, multiplication, and negation have close analogues for vectors, operation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalue
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by \lambda, is the factor by which the eigenvector is scaled. Geometrically, an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction in which it is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed. Loosely speaking, in a multidimensional vector space, the eigenvector is not rotated. Formal definition If is a linear transformation from a vector space over a field into itself and is a nonzero vector in , then is an eigenvector of if is a scalar multiple of . This can be written as T(\mathbf) = \lambda \mathbf, where is a scalar in , known as the eigenvalue, characteristic value, or characteristic roo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |