|
Pricing Model
In financial economics, asset pricing refers to a formal treatment and development of two main pricing principles, outlined below, together with the resultant models. There have been many models developed for different situations, but correspondingly, these stem from either general equilibrium asset pricing or rational asset pricing, the latter corresponding to risk neutral pricing. Investment theory, which is near synonymous, encompasses the body of knowledge used to support the decision-making process of choosing investments, and the asset pricing models are then applied in determining the asset-specific required rate of return on the investment in question, or in pricing derivatives on these, for trading or hedging. (See also .) General Equilibrium Asset Pricing Under General equilibrium theory prices are determined through market pricing by supply and demand. Here asset prices jointly satisfy the requirement that the quantities of each asset supplied and the quan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Capital Asset Pricing Model
In finance, the capital asset pricing model (CAPM) is a model used to determine a theoretically appropriate required rate of return of an asset, to make decisions about adding assets to a well-diversified portfolio. The model takes into account the asset's sensitivity to non-diversifiable risk (also known as systematic risk or market risk), often represented by the quantity beta (β) in the financial industry, as well as the expected return of the market and the expected return of a theoretical risk-free asset. CAPM assumes a particular form of utility functions (in which only first and second moments matter, that is risk is measured by variance, for example a quadratic utility) or alternatively asset returns whose probability distributions are completely described by the first two moments (for example, the normal distribution) and zero transaction costs (necessary for diversification to get rid of all idiosyncratic risk). Under these conditions, CAPM shows that the cost of eq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ho–Lee Model
In financial mathematics, the Ho–Lee model is a short-rate model widely used in the pricing of bond options, swaptions and other interest rate derivatives, and in modeling future interest rates. It was developed in 1986 by Thomas Ho and Sang Bin Lee. Under this model, the short rate follows a normal process: :dr_t = \theta_t\, dt + \sigma\, dW_t The model can be calibrated to market data by implying the form of \theta_t from market prices, meaning that it can exactly return the price of bonds comprising the yield curve. This calibration, and subsequent valuation of bond options, swaptions and other interest rate derivatives, is typically performed via a binomial lattice based model. Closed form valuations of bonds, and " Black-like" bond option formulae are also available.Graeme West, (2010)''Interest Rate Derivatives'', Financial Modelling Agency. As the model generates a symmetric ("bell shaped") distribution of rates in the future, negative rates are possible. Further, i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
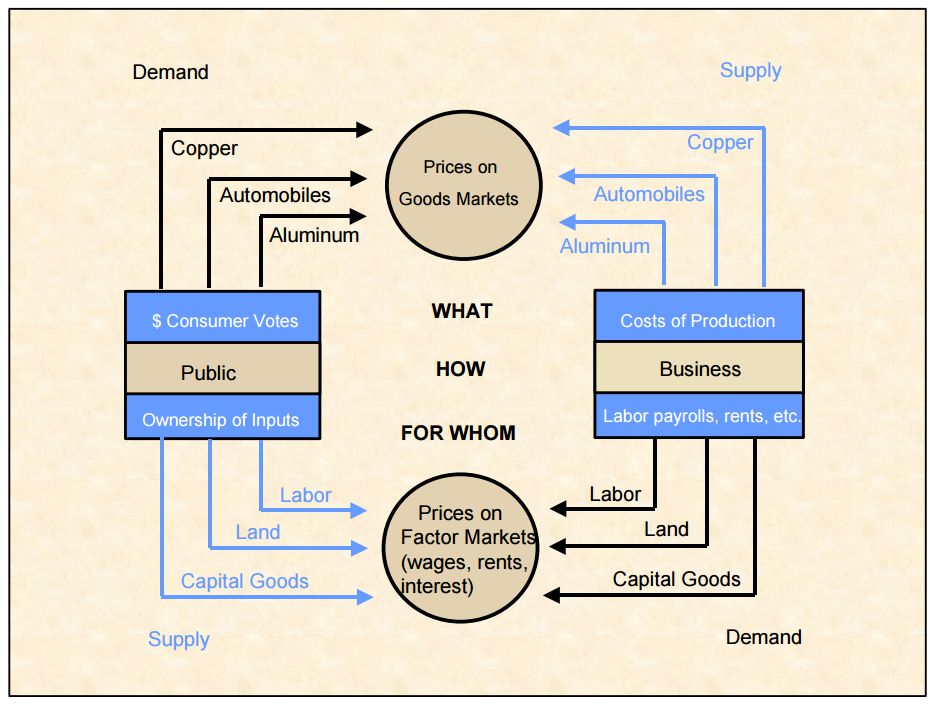
Price
A price is the (usually not negative) quantity of payment or compensation given by one party to another in return for goods or services. In some situations, the price of production has a different name. If the product is a "good" in the commercial exchange, the payment for this product will likely be called its "price". However, if the product is "service", there will be other possible names for this product's name. For example, the graph on the bottom will show some situations A good's price is influenced by production costs, supply of the desired item, and demand for the product. A price may be determined by a monopolist or may be imposed on the firm by market conditions. Price can be quoted to currency, quantities of goods or vouchers. * In modern economies, prices are generally expressed in units of some form of currency. (More specifically, for raw materials they are expressed as currency per unit weight, e.g. euros per kilogram or Rands per KG.) * Although prices ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Financial Economics
Financial economics, also known as finance, is the branch of economics characterized by a "concentration on monetary activities", in which "money of one type or another is likely to appear on ''both sides'' of a trade".William F. Sharpe"Financial Economics", in Its concern is thus the interrelation of financial variables, such as share prices, interest rates and exchange rates, as opposed to those concerning the real economy. It has two main areas of focus: Merton H. Miller, (1999). The History of Finance: An Eyewitness Account, ''Journal of Portfolio Management''. Summer 1999. asset pricing, commonly known as "Investments", and corporate finance; the first being the perspective of providers of capital, i.e. investors, and the second of users of capital. It thus provides the theoretical underpinning for much of finance. The subject is concerned with "the allocation and deployment of economic resources, both spatially and across time, in an uncertain environment".See Fama and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Corporate Finance
Corporate finance is the area of finance that deals with the sources of funding, the capital structure of corporations, the actions that managers take to increase the Value investing, value of the firm to the shareholders, and the tools and analysis used to allocate financial resources. The primary goal of corporate finance is to Shareholder value, maximize or increase valuation (finance), shareholder value. Correspondingly, corporate finance comprises two main sub-disciplines. Capital budgeting is concerned with the setting of criteria about which value-adding projects should receive investment funding, and whether to finance that investment with ownership equity, equity or debt capital. Working capital management is the management of the company's monetary funds that deal with the short-term business operations, operating balance of current assets and Current liability, current liabilities; the focus here is on managing cash, inventory, inventories, and short-term borrowing an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
LIBOR Market Model
The LIBOR market model, also known as the BGM Model (Brace Gatarek Musiela Model, in reference to the names of some of the inventors) is a financial model of interest rates. It is used for pricing interest rate derivatives, especially exotic derivatives like Bermudan swaptions, ratchet caps and floors, target redemption notes, autocaps, zero coupon swaptions, constant maturity swaps and spread options, among many others. The quantities that are modeled, rather than the short rate or instantaneous forward rates (like in the Heath–Jarrow–Morton framework) are a set of forward rates (also called forward LIBORs), which have the advantage of being directly observable in the market, and whose volatilities are naturally linked to traded contracts. Each forward rate is modeled by a lognormal process under its forward measure, i.e. a Black model leading to a Black formula for interest rate caps. This formula is the market standard to quote cap prices in terms of implied volatilities, he ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heath–Jarrow–Morton Framework
The Heath–Jarrow–Morton (HJM) framework is a general framework to model the evolution of interest rate curves – instantaneous forward rate curves in particular (as opposed to simple forward rates). When the volatility and drift of the instantaneous forward rate are assumed to be deterministic, this is known as the Gaussian Heath–Jarrow–Morton (HJM) model of forward rates. For direct modeling of simple forward rates the Brace–Gatarek–Musiela model represents an example. The HJM framework originates from the work of David Heath, Robert A. Jarrow, and Andrew Morton in the late 1980s, especially ''Bond pricing and the term structure of interest rates: a new methodology'' (1987) – working paper, Cornell University, and ''Bond pricing and the term structure of interest rates: a new methodology'' (1989) – working paper (revised ed.), Cornell University. It has its critics, however, with Paul Wilmott describing it as "...actually just a big rug for istake ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chen Model
In finance, the Chen model is a mathematical model describing the evolution of interest rates. It is a type of "three-factor model" (short-rate model) as it describes interest rate movements as driven by three sources of market risk. It was the first stochastic mean and stochastic volatility model and it was published in 1994 by Lin Chen, economist, theoretical physicist and former lecturer/professor at Beijing Institute of Technology, Yonsei University of Korea, and Nanyang Tech University of Singapore. The dynamics of the instantaneous interest rate are specified by the stochastic differential equations: : dr_t = \kappa(\theta_t-r_t)\,dt + \sqrt\,\sqrt\, dW_1, : d \theta_t = \nu(\zeta-\theta_t)\,dt + \alpha\,\sqrt\, dW_2, : d \sigma_t = \mu(\beta-\sigma_t)\,dt + \eta\,\sqrt\, dW_3. In an authoritative review of modern finance (''Continuous-Time Methods in Finance: A Review and an Assessment''), the Chen model is listed along with the models of Robert C. Merton, Oldrich Vasi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Longstaff–Schwartz Model
A short-rate model, in the context of interest rate derivatives, is a mathematical model that describes the future evolution of interest rates by describing the future evolution of the short rate, usually written r_t \,. The short rate Under a short rate model, the stochastic state variable is taken to be the instantaneous spot rate. The short rate, r_t \,, then, is the ( continuously compounded, annualized) interest rate at which an entity can borrow money for an infinitesimally short period of time from time t. Specifying the current short rate does not specify the entire yield curve. However, no-arbitrage arguments show that, under some fairly relaxed technical conditions, if we model the evolution of r_t \, as a stochastic process under a risk-neutral measure Q, then the price at time t of a zero-coupon bond maturing at time T with a payoff of 1 is given by : P(t,T) = \operatorname^Q\left \mathcal_t \right where \mathcal is the natural filtration for the process. The inter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kalotay–Williams–Fabozzi Model
A short-rate model, in the context of interest rate derivatives, is a mathematical model that describes the future evolution of interest rates by describing the future evolution of the short rate, usually written r_t \,. The short rate Under a short rate model, the stochastic state variable is taken to be the instantaneous spot rate. The short rate, r_t \,, then, is the (Compound interest#Continuous compounding, continuously compounded, annualized) interest rate at which an entity can borrow money for an infinitesimally short period of time from time t. Specifying the current short rate does not specify the entire yield curve. However, arbitrage, no-arbitrage arguments show that, under some fairly relaxed technical conditions, if we model the evolution of r_t \, as a stochastic process under a risk-neutral measure Q, then the price at time t of a zero-coupon bond maturing at time T with a payoff of 1 is given by : P(t,T) = \operatorname^Q\left[\left. \exp \ \mathcal_t \right], wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.png "Click for more on -> Longstaff–Schwartz Model")