|
Platonic Solid
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent (identical in shape and size) regular polygons (all angles congruent and all edges congruent), and the same number of faces meet at each vertex. There are only five such polyhedra: Geometers have studied the Platonic solids for thousands of years. They are named for the ancient Greek philosopher Plato who hypothesized in one of his dialogues, the ''Timaeus'', that the classical elements were made of these regular solids. History The Platonic solids have been known since antiquity. It has been suggested that certain carved stone balls created by the late Neolithic people of Scotland represent these shapes; however, these balls have rounded knobs rather than being polyhedral, the numbers of knobs frequently differed from the numbers of vertices of the Platonic solids, there is no ball whose knobs match the 20 vertic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mysterium Cosmographicum Solar System Model
Mysterium may refer to: * ''Mysterium'' (John Zorn album), 2005 * ''Mysterium'' (Manilla Road album), 2013 * ''Mysterium'' (board game), a cooperative board game designed by Oleksandr Nevskiy and Oleg Sidorenko * ''Mysterium'' (novel), an alternate history novel by Robert Charles Wilson * ''Mysterium'' (Scriabin), an unfinished work by the Russian composer Alexander Scriabin *''Mysterium'', seventh part of composer Georges Lentz’ musical cycle '' Caeli enarrant...'' * ''Mysterium'' (video game), a video game published in 1991 * An annual conference concerned with the ''Myst'' series of computer games * Greco-Roman mysteries, religious schools for which participation was reserved to initiates See also * Mysteria (other) * Mystery (other) * Mysterium fidei (other) ''Mysterium fidei'' may refer to: * ''Mysterium fidei'' (encyclical), 1965 papal encyclical on the Eucharist by Pope Paul VI * "The mystery of faith" or "a mystery of faith", phrase ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Classical Element
Classical elements typically refer to earth, water, air, fire, and (later) aether which were proposed to explain the nature and complexity of all matter in terms of simpler substances. Ancient cultures in Greece, Tibet, and India had similar lists which sometimes referred, in local languages, to "air" as "wind" and the fifth element as "void". These different cultures and even individual philosophers had widely varying explanations concerning their attributes and how they related to observable phenomena as well as cosmology. Sometimes these theories overlapped with mythology and were personified in deities. Some of these interpretations included atomism (the idea of very small, indivisible portions of matter), but other interpretations considered the elements to be divisible into infinitely small pieces without changing their nature. While the classification of the material world in ancient Indian, Hellenistic Egypt, and ancient Greece into Air, Earth, Fire and Water was ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
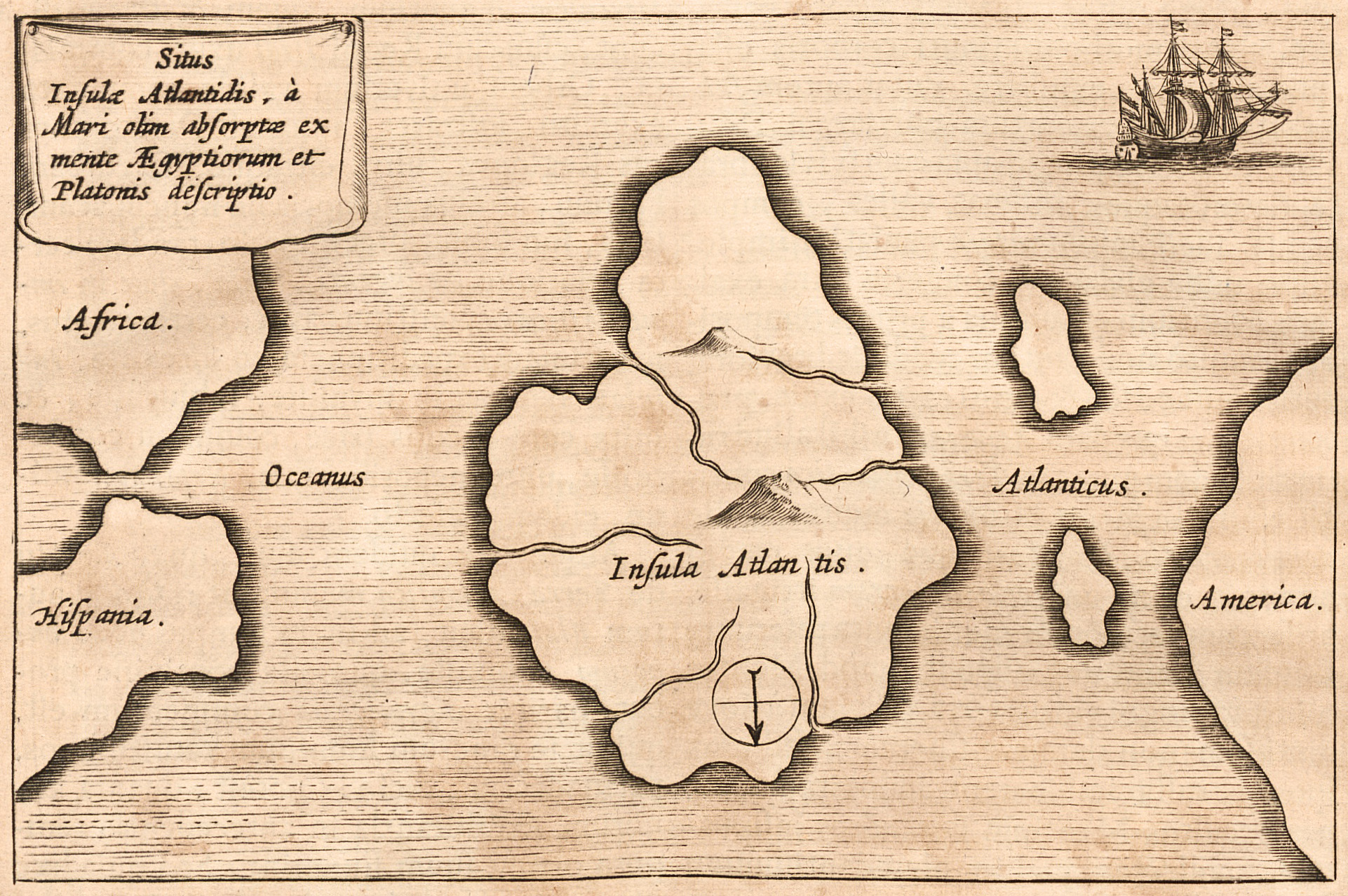
Timaeus (dialogue)
''Timaeus'' (; grc-gre, Τίμαιος, Timaios, ) is one of Plato's dialogues, mostly in the form of long monologues given by Critias and Timaeus, written 360 BC. The work puts forward reasoning on the possible nature of the physical world and human beings and is followed by the dialogue ''Critias''. Participants in the dialogue include Socrates, Timaeus, Hermocrates, and Critias. Some scholars believe that it is not the Critias of the Thirty Tyrants who appears in this dialogue, but his grandfather, who is also named Critias. It has been suggested from some traditions (Diogenes Laertius (VIII 85) from Hermippus of Smyrna (3rd century BC) and Timon of Phlius ( 320 – 235 BC)) that ''Timaeus'' was influenced by a book about Pythagoras, written by Philolaus, although this assertion is generally considered false. Introduction The dialogue takes place the day after Socrates described his ideal state. In Plato's works, such a discussion occurs in the ''Republic''. Socrates fe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plato
Plato ( ; grc-gre, Πλάτων ; 428/427 or 424/423 – 348/347 BC) was a Greek philosopher born in Athens during the Classical period in Ancient Greece. He founded the Platonist school of thought and the Academy, the first institution of higher learning on the European continent. Along with his teacher, Socrates, and his student, Aristotle, Plato is a central figure in the history of Ancient Greek philosophy and the Western and Middle Eastern philosophies descended from it. He has also shaped religion and spirituality. The so-called neoplatonism of his interpreter Plotinus greatly influenced both Christianity (through Church Fathers such as Augustine) and Islamic philosophy (through e.g. Al-Farabi). In modern times, Friedrich Nietzsche diagnosed Western culture as growing in the shadow of Plato (famously calling Christianity "Platonism for the masses"), while Alfred North Whitehead famously said: "the safest general characterization of the European philosophical tra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Games Column
Over a period of 24 years (January 1957 – December 1980), Martin Gardner wrote 288 consecutive monthly "Mathematical Games" columns for ''Scientific American'' magazine. During the next years, through June 1986, Gardner wrote 9 more columns, bringing his total to 297, as other authors wrote most of the "Mathematical Games" columns. The table below lists Gardner's columns. Twelve of Gardner's columns provided the cover art for that month's magazine, indicated by "over in the table with a hyperlink to the cover. Other articles by Gardner Gardner wrote 5 other articles for ''Scientific American''. His flexagon article in December 1956 was in all but name the first article in the series of ''Mathematical Games'' columns and led directly to the series which began the following month. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Martin Gardner
Martin Gardner (October 21, 1914May 22, 2010) was an American popular mathematics and popular science writer with interests also encompassing scientific skepticism, micromagic, philosophy, religion, and literatureespecially the writings of Lewis Carroll, L. Frank Baum, and G. K. Chesterton.Martin (2010) He was also a leading authority on Lewis Carroll. ''The Annotated Alice'', which incorporated the text of Carroll's two Alice books, was his most successful work and sold over a million copies. He had a lifelong interest in magic and illusion and in 1999, MAGIC magazine named him as one of the "100 Most Influential Magicians of the Twentieth Century". He was considered the doyen of American puzzlers. He was a prolific and versatile author, publishing more than 100 books. Gardner was best known for creating and sustaining interest in recreational mathematicsand by extension, mathematics in generalthroughout the latter half of the 20th century, principally through his "Mathema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometer
A geometer is a mathematician whose area of study is geometry. Some notable geometers and their main fields of work, chronologically listed, are: 1000 BCE to 1 BCE * Baudhayana (fl. c. 800 BC) – Euclidean geometry, geometric algebra * Manava (c. 750 BC–690 BC) – Euclidean geometry * Thales of Miletus (c. 624 BC – c. 546 BC) – Euclidean geometry * Pythagoras (c. 570 BC – c. 495 BC) – Euclidean geometry, Pythagorean theorem * Zeno of Elea (c. 490 BC – c. 430 BC) – Euclidean geometry * Hippocrates of Chios (born c. 470 – 410 BC) – first systematically organized '' Stoicheia – Elements'' (geometry textbook) * Mozi (c. 468 BC – c. 391 BC) * Plato (427–347 BC) * Theaetetus (c. 417 BC – 369 BC) * Autolycus of Pitane (360–c. 290 BC) – astronomy, spherical geometry * Euclid (fl. 300 BC) – '' Elements'', Euclidean geometry (sometimes called the "father of geometry") * Apollonius of Perga (c. 262 BC – c. 190 BC) – Euclidean geometry, conic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Icosahedron
In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes and . The plural can be either "icosahedra" () or "icosahedrons". There are infinitely many non- similar shapes of icosahedra, some of them being more symmetrical than others. The best known is the (convex, non- stellated) regular icosahedron—one of the Platonic solids—whose faces are 20 equilateral triangles. Regular icosahedra There are two objects, one convex and one nonconvex, that can both be called regular icosahedra. Each has 30 edges and 20 equilateral triangle faces with five meeting at each of its twelve vertices. Both have icosahedral symmetry. The term "regular icosahedron" generally refers to the convex variety, while the nonconvex form is called a ''great icosahedron''. Convex regular icosahedron The convex regular icosahedron is usually referred to simply as the ''regular icosahedron'', one of the five regular Platonic solids, and is represented by its Schläfli symbol , con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
