|
Phase Noise
In signal processing, phase noise is the frequency-domain representation of random fluctuations in the phase of a waveform, corresponding to time-domain deviations from perfect periodicity (jitter). Generally speaking, radio-frequency engineers speak of the phase noise of an oscillator, whereas digital-system engineers work with the jitter of a clock. Definitions Historically there have been two conflicting yet widely used definitions for phase noise. Some authors define phase noise to be the spectral density of a signal's phase only, while the other definition refers to the phase spectrum (which pairs up with the amplitude spectrum) resulting from the spectral estimation of the signal itself. Both definitions yield the same result at offset frequencies well removed from the carrier. At close-in offsets however, the two definitions differ. The IEEE defines phase noise as where the "phase instability" is the one-sided spectral density of a signal's phase deviation. Although ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
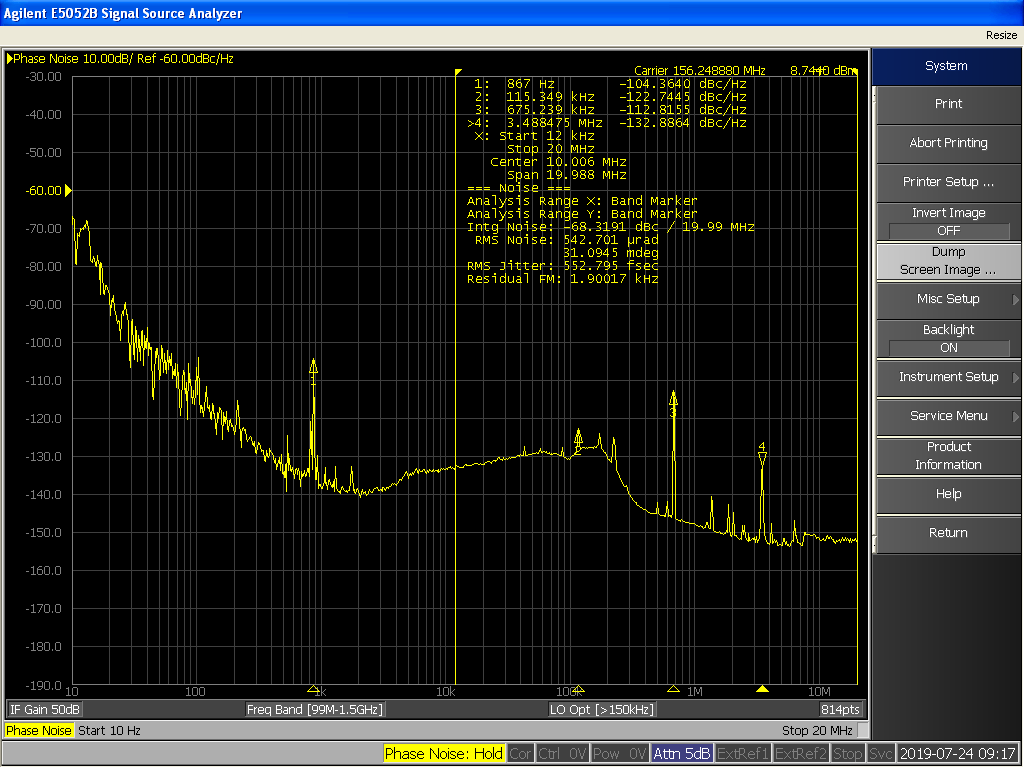
Phase Noise Measured In Ssa
Phase or phases may refer to: Science *State of matter, or phase, one of the distinct forms in which matter can exist *Phase (matter), a region of space throughout which all physical properties are essentially uniform *Phase space, a mathematical space in which each possible state of a physical system is represented by a point — this equilibrium point is also referred to as a "microscopic state" **Phase space formulation, a formulation of quantum mechanics in phase space *Phase (waves), the position of a point in time (an instant) on a waveform cycle **Instantaneous phase, generalization for both cyclic and non-cyclic phenomena * AC phase, the phase offset between alternating current electric power in multiple conducting wires **Single-phase electric power, distribution of AC electric power in a system where the voltages of the supply vary in unison **Three-phase electric power, a common method of AC electric power generation, transmission, and distribution *Phase problem, the l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power (physics)
In physics, power is the amount of energy transferred or converted per unit time. In the International System of Units, the unit of power is the watt, equal to one joule per second. In older works, power is sometimes called ''activity''. Power is a scalar quantity. Power is related to other quantities; for example, the power involved in moving a ground vehicle is the product of the aerodynamic drag plus traction force on the wheels, and the velocity of the vehicle. The output power of a motor is the product of the torque that the motor generates and the angular velocity of its output shaft. Likewise, the power dissipated in an electrical element of a circuit is the product of the current flowing through the element and of the voltage across the element. Definition Power is the rate with respect to time at which work is done; it is the time derivative of work: P =\frac where is power, is work, and is time. If a constant force F is applied throughout a distance x, the wor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Local Oscillator
In electronics, a local oscillator (LO) is an electronic oscillator used with a mixer to change the frequency of a signal. This frequency conversion process, also called heterodyning, produces the sum and difference frequencies from the frequency of the local oscillator and frequency of the input signal. Processing a signal at a fixed frequency gives a radio receiver improved performance. In many receivers, the function of local oscillator and mixer is combined in one stage called a " converter" - this reduces the space, cost, and power consumption by combining both functions into one active device. Applications Local oscillators are used in the superheterodyne receiver, the most common type of radio receiver circuit. They are also used in many other communications circuits such as modems, cable television set top boxes, frequency division multiplexing systems used in telephone trunklines, microwave relay systems, telemetry systems, atomic clocks, radio telescopes, and milita ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectrum Analyzer
A spectrum analyzer measures the magnitude of an input signal versus frequency within the full frequency range of the instrument. The primary use is to measure the power of the spectrum of known and unknown signals. The input signal that most common spectrum analyzers measure is electrical; however, spectral compositions of other signals, such as acoustic pressure waves and optical light waves, can be considered through the use of an appropriate transducer. Spectrum analyzers for other types of signals also exist, such as optical spectrum analyzers which use direct optical techniques such as a monochromator to make measurements. By analyzing the spectra of electrical signals, dominant frequency, power, distortion, harmonics, bandwidth, and other spectral components of a signal can be observed that are not easily detectable in time domain waveforms. These parameters are useful in the characterization of electronic devices, such as wireless transmitters. The display of a spectru ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Root-mean-square
In mathematics and its applications, the root mean square of a set of numbers x_i (abbreviated as RMS, or rms and denoted in formulas as either x_\mathrm or \mathrm_x) is defined as the square root of the mean square (the arithmetic mean of the squares) of the set. The RMS is also known as the quadratic mean (denoted M_2) and is a particular case of the generalized mean. The RMS of a continuously varying function (denoted f_\mathrm) can be defined in terms of an integral of the squares of the instantaneous values during a cycle. For alternating electric current, RMS is equal to the value of the constant direct current that would produce the same power dissipation in a resistive load. In estimation theory, the root-mean-square deviation of an estimator is a measure of the imperfection of the fit of the estimator to the data. Definition The RMS value of a set of values (or a continuous-time waveform) is the square root of the arithmetic mean of the squares of the values, or th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leeson's Equation
Leeson's equation is an empirical expression that describes an oscillator's phase noise spectrum. Leeson's expression for single-sideband (SSB) phase noise in dBc/Hz (decibels relative to output level per hertz) and augmented for flicker noise: :L(f_m) = 10 \log \bigg \frac \bigg( \bigg(\frac\bigg)^2 + 1\bigg)\bigg(\frac + 1\bigg)\bigg(\frac\bigg) \bigg/math> where is the output frequency, is the loaded quality factor, is the offset from the output frequency (Hz), is the corner frequency, is the noise factor of the amplifier, is Boltzmann's constant in joules/kelvin, is absolute temperature in kelvins, and is the available power at the sustaining amplifier input.https://www.ieee.li/pdf/essay/phase_noise_basics.pdf There is often misunderstanding around Leeson's equation, even in text books. In the 1966 paper, Leeson stated correctly that " is the signal level at the oscillator active element input" (often referred to as the power through the resonator now, strictly speaki ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
1/f Noise
Pink noise or noise is a signal or process with a frequency spectrum such that the power spectral density (power per frequency interval) is inversely proportional to the frequency of the signal. In pink noise, each octave interval (halving or doubling in frequency) carries an equal amount of noise energy. Pink noise sounds like a waterfall. It is often used to tune loudspeaker systems in professional audio. Pink noise is one of the most commonly observed signals in biological systems. The name arises from the pink appearance of visible light with this power spectrum. This is in contrast with white noise which has equal intensity per frequency interval. Definition Within the scientific literature, the term 1/f noise is sometimes used loosely to refer to any noise with a power spectral density of the form S(f) \propto \frac, where ''f'' is frequency, and 0 < α < 2, with exponent α usually close to 1. One-dimensional signals with α = 1 are usually called pink noise. The f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oscillator Phase Noise
Oscillators produce various levels of phase noise, or variations from perfect periodicity. Viewed as an additive noise, phase noise increases at frequencies close to the oscillation frequency or its harmonics. With the additive noise being close to the oscillation frequency, it cannot be removed by filtering without also removing the oscillation signal. All well-designed nonlinear oscillators have stable limit cycles, meaning that if perturbed, the oscillator will naturally return to its periodic limit cycle. When perturbed, the oscillator responds by spiraling back into the limit cycle, but not necessarily at the same phase. This is because the oscillator is autonomous; it has no stable time reference. The phase is free to drift. As a result, any perturbation of the oscillator causes the phase to drift, which explains why the noise produced by an oscillator is predominantly in phase. Oscillator voltage noise and phase-noise spectra There are two different ways commonly used ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cyclostationary Noise
A cyclostationary process is a signal having statistical properties that vary cyclically with time. A cyclostationary process can be viewed as multiple interleaved stationary processes. For example, the maximum daily temperature in New York City can be modeled as a cyclostationary process: the maximum temperature on July 21 is statistically different from the temperature on December 20; however, it is a reasonable approximation that the temperature on December 20 of different years has identical statistics. Thus, we can view the random process composed of daily maximum temperatures as 365 interleaved stationary processes, each of which takes on a new value once per year. Definition There are two differing approaches to the treatment of cyclostationary processes. The probabilistic approach is to view measurements as an instance of a stochastic process. As an alternative, the deterministic approach is to view the measurements as a single time series, from which a probability distri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Process
In probability theory and related fields, a stochastic () or random process is a mathematical object usually defined as a family of random variables. Stochastic processes are widely used as mathematical models of systems and phenomena that appear to vary in a random manner. Examples include the growth of a bacterial population, an electrical current fluctuating due to thermal noise, or the movement of a gas molecule. Stochastic processes have applications in many disciplines such as biology, chemistry, ecology, neuroscience, physics, image processing, signal processing, control theory, information theory, computer science, cryptography and telecommunications. Furthermore, seemingly random changes in financial markets have motivated the extensive use of stochastic processes in finance. Applications and the study of phenomena have in turn inspired the proposal of new stochastic processes. Examples of such stochastic processes include the Wiener process or Brownian motion process, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
White Noise
In signal processing, white noise is a random signal having equal intensity at different frequencies, giving it a constant power spectral density. The term is used, with this or similar meanings, in many scientific and technical disciplines, including physics, acoustical engineering, telecommunications, and statistical forecasting. White noise refers to a statistical model for signals and signal sources, rather than to any specific signal. White noise draws its name from white light, although light that appears white generally does not have a flat power spectral density over the visible band. In discrete time, white noise is a discrete signal whose samples are regarded as a sequence of serially uncorrelated random variables with zero mean and finite variance; a single realization of white noise is a random shock. Depending on the context, one may also require that the samples be independent and have identical probability distribution (in other words independent and iden ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flicker Noise
Flicker noise is a type of electronic noise with a 1/''f'' power spectral density. It is therefore often referred to as 1/''f'' noise or pink noise, though these terms have wider definitions. It occurs in almost all electronic devices and can show up with a variety of other effects, such as impurities in a conductive channel, generation and recombination noise in a transistor due to base current, and so on. Properties 1/''f'' noise in current or voltage is usually related to a direct current, as resistance fluctuations are transformed to voltage or current fluctuations by Ohm's law. There is also a 1/''f'' component in resistors with no direct current through them, likely due to temperature fluctuations modulating the resistance. This effect is not present in manganin, as it has negligible temperature coefficient of resistance. In electronic devices, it shows up as a low-frequency phenomenon, as the higher frequencies are overshadowed by white noise from other sources. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
