|
Parastatistics
In quantum mechanics and statistical mechanics, parastatistics is a hypothetical alternative to the established particle statistics models (Bose–Einstein statistics, Fermi–Dirac statistics and Maxwell–Boltzmann statistics). Other alternatives include anyonic statistics and braid statistics, both of these involving lower spacetime dimensions. Herbert S. Green is credited with the creation of parastatistics in 1953.H. S. Green, "A Generalized Method of Field Quantization", Phys. Rev. 90, 270–273 (1953). The particles predicted by parastatistics have not been experimentally observed. Formalism Consider the operator algebra of a system of ''N'' identical particles. This is a star-algebra, *-algebra. There is an ''SN'' group (symmetric group of order ''N'') Group action (mathematics), acting upon the operator algebra with the intended interpretation of permutation, permuting the ''N'' particles. Quantum mechanics requires focus on observables having a physical meaning, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Braid Statistics
In mathematics and theoretical physics, braid statistics is a generalization of the Spin–statistics theorem, spin statistics of bosons and fermions based on the concept of braid group. While for fermions (bosons) the corresponding statistics is associated to a phase gain of \pi (2 \pi) under the exchange of identical particles, a particle with braid statistics leads to a rational fraction of \pi under such exchange or even a non-trivial unitary transformation in the Hilbert space (see Anyon#Non-abelian anyons, non-Abelian anyons). A similar notion exists using a loop braid group. Plektons Braid statistics are applicable to theoretical particles such as the two-dimensional Anyon, anyons and plektons. A plekton is a hypothetical type of particle that obeys a different style of quantum statistics, statistics with respect to the interchange of identical particles. It obeys the causality rules of algebraic quantum field theory, where only observable quantities need to commute a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
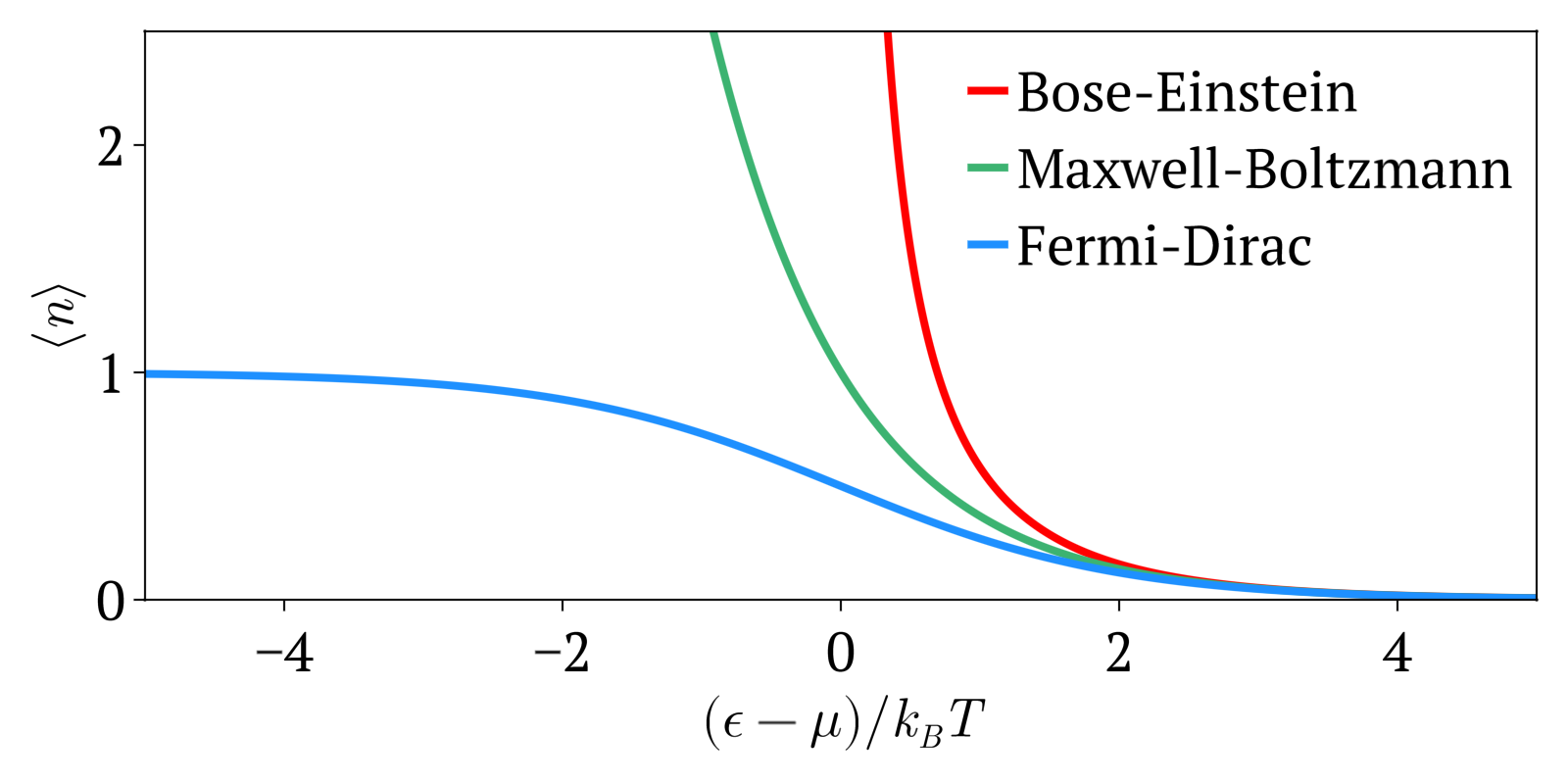
Bose–Einstein Statistics
In quantum statistics, Bose–Einstein statistics (B–E statistics) describes one of two possible ways in which a collection of non-interacting identical particles may occupy a set of available discrete energy states at thermodynamic equilibrium. The aggregation of particles in the same state, which is a characteristic of particles obeying Bose–Einstein statistics, accounts for the cohesive streaming of laser light and the frictionless creeping of superfluid helium. The theory of this behaviour was developed (1924–25) by Satyendra Nath Bose, who recognized that a collection of identical and indistinguishable particles could be distributed in this way. The idea was later adopted and extended by Albert Einstein in collaboration with Bose. Bose–Einstein statistics apply only to particles that do not follow the Pauli exclusion principle restrictions. Particles that follow Bose-Einstein statistics are called bosons, which have integer values of spin. In contrast, particles ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermi–Dirac Statistics
Fermi–Dirac statistics is a type of quantum statistics that applies to the physics of a system consisting of many non-interacting, identical particles that obey the Pauli exclusion principle. A result is the Fermi–Dirac distribution of particles over energy states. It is named after Enrico Fermi and Paul Dirac, each of whom derived the distribution independently in 1926. Fermi–Dirac statistics is a part of the field of statistical mechanics and uses the principles of quantum mechanics. Fermi–Dirac statistics applies to identical and indistinguishable particles with half-integer spin (1/2, 3/2, etc.), called fermions, in thermodynamic equilibrium. For the case of negligible interaction between particles, the system can be described in terms of single-particle energy states. A result is the Fermi–Dirac distribution of particles over these states where no two particles can occupy the same state, which has a considerable effect on the properties of the system. Fermi� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anyonic Statistics
In physics, an anyon is a type of quasiparticle so far observed only in two-dimensional systems. In three-dimensional systems, only two kinds of elementary particles are seen: fermions and bosons. Anyons have statistical properties intermediate between fermions and bosons. In general, the operation of exchanging two identical particles, although it may cause a global phase shift, cannot affect observables. Anyons are generally classified as ''abelian'' or ''non-abelian''. Abelian anyons, detected by two experiments in 2020, play a major role in the fractional quantum Hall effect. Introduction The statistical mechanics of large many-body systems obeys laws described by Maxwell–Boltzmann statistics. Quantum statistics is more complicated because of the different behaviors of two different kinds of particles called fermions and bosons. In two-dimensional systems, however, there is a third type of particle, called an anyon. In a two-dimensional world, two identical anyons c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin–statistics Theorem
The spin–statistics theorem proves that the observed relationship between the intrinsic spin of a particle (angular momentum not due to the orbital motion) and the quantum particle statistics of collections of such particles is a consequence of the mathematics of quantum mechanics. According to the theorem, the many-body wave function for elementary particles with integer spin ( bosons) is symmetric under the exchange of any two particles, whereas for particles with half-integer spin ( fermions), the wave function is antisymmetric under such an exchange. A consequence of the theorem is that non-interacting particles with integer spin obey Bose–Einstein statistics, while those with half-integer spin obey Fermi–Dirac statistics. Background The statistics of indistinguishable particles is among the most fundamental of physical effects. The Pauli exclusion principle that every occupied quantum state contains at most one fermion controls the formation of matter. The basic bu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boson
In particle physics, a boson ( ) is a subatomic particle whose spin quantum number has an integer value (0, 1, 2, ...). Bosons form one of the two fundamental classes of subatomic particle, the other being fermions, which have half odd-integer spin (1/2, 3/2, 5/2, ...). Every observed subatomic particle is either a boson or a fermion. Paul Dirac coined the name ''boson'' to commemorate the contribution of Satyendra Nath Bose, an Indian physicist. Some bosons are elementary particles occupying a special role in particle physics, distinct from the role of fermions (which are sometimes described as the constituents of "ordinary matter"). Certain elementary bosons (e.g. gluons) act as force carriers, which give rise to forces between other particles, while one (the Higgs boson) contributes to the phenomenon of mass. Other bosons, such as mesons, are composite particles made up of smaller constituents. Outside the realm of particle physics, multiple identical composite bosons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science. Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and Microscopic scale, (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Classical mechanics can be derived from quantum mechanics as an approximation that is valid at ordinary scales. Quantum systems have Bound state, bound states that are Quantization (physics), quantized to Discrete mathematics, discrete values of energy, momentum, angular momentum, and ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Observable
In physics, an observable is a physical property or physical quantity that can be measured. In classical mechanics, an observable is a real-valued "function" on the set of all possible system states, e.g., position and momentum. In quantum mechanics, an observable is an operator, or gauge, where the property of the quantum state can be determined by some sequence of operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value. Physically meaningful observables must also satisfy transformation laws that relate observations performed by different observers in different frames of reference. These transformation laws are automorphisms of the state space, that is bijective transformations that preserve certain mathematical properties of the space in question. Quantum mechanics In quantum mechanics, observables manifest as self-adjoint operators on a separable complex Hilbert space ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory. Group theory The commutator of two elements, and , of a group , is the element : . This element is equal to the group's identity if and only if and commute (that is, if and only if ). The set of all commutators of a group is not in general closed under the group operation, but the subgroup of ''G'' generated by all commutators is closed and is called the ''derived group'' or the '' commutator subgroup'' of ''G''. Commutators are used to define nilpotent and solvable groups and the largest abelian quotient group. The definition of the commutator above is used throughout this article, but many group theorists define the commutator as : . Using the first definition, this can be expressed as . Identities (group theory) Commutator identities are an important tool in group th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Duffin–Kemmer–Petiau Algebra
In mathematical physics, the Duffin–Kemmer–Petiau (DKP) algebra, introduced by R.J. Duffin, Nicholas Kemmer and G. Petiau, is the algebra which is generated by the Duffin–Kemmer–Petiau matrices. These matrices form part of the Duffin–Kemmer–Petiau equation that provides a relativistic description of spin-0 and spin-1 particles. The DKP algebra is also referred to as the meson algebra. Defining relations The Duffin–Kemmer–Petiau matrices have the defining relationSee introductory section of: :\beta^ \beta^ \beta^ + \beta^ \beta^ \beta^ = \beta^ \eta^ + \beta^ \eta^ where \eta^ stand for a constant diagonal matrix. The Duffin–Kemmer–Petiau matrices \beta for which \eta^ consists in diagonal elements (+1,-1,...,-1) form part of the Duffin–Kemmer–Petiau equation. Five-dimensional DKP matrices can be represented as:See for example : \beta^ = \begin 0&1&0&0&0\\ 1&0&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&0 \end , \quad \beta^ = \begin 0&0&-1&0&0\\ 0&0&0&0&0\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graded Algebra
In mathematics, in particular abstract algebra, a graded ring is a ring such that the underlying additive group is a direct sum of abelian groups R_i such that . The index set is usually the set of nonnegative integers or the set of integers, but can be any monoid. The direct sum decomposition is usually referred to as gradation or grading. A graded module is defined similarly (see below for the precise definition). It generalizes graded vector spaces. A graded module that is also a graded ring is called a graded algebra. A graded ring could also be viewed as a graded -algebra. The associativity is not important (in fact not used at all) in the definition of a graded ring; hence, the notion applies to non-associative algebras as well; e.g., one can consider a graded Lie algebra. First properties Generally, the index set of a graded ring is assumed to be the set of nonnegative integers, unless otherwise explicitly specified. This is the case in this article. A graded r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |