|
Optimal Play
In game theory, the best response is the strategy (or strategies) which produces the most favorable outcome for a player, taking other players' strategies as given (; ). The concept of a best response is central to John Nash's best-known contribution, the Nash equilibrium, the point at which each player in a game has selected the best response (or one of the best responses) to the other players' strategies . Correspondence Reaction correspondences, also known as best response correspondences, are used in the proof of the existence of mixed strategy Nash equilibria (, Section 1.3.B; , Section 2.2). Reaction correspondences are not "reaction functions" since functions must only have one value per argument, and many reaction correspondences will be undefined, i.e., a vertical line, for some opponent strategy choice. One constructs a correspondence b(\cdot), for each player from the set of opponent strategy profiles into the set of the player's strategies. So, for any given set o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Game Theory
Game theory is the study of mathematical models of strategic interactions among rational agents. Myerson, Roger B. (1991). ''Game Theory: Analysis of Conflict,'' Harvard University Press, p.&nbs1 Chapter-preview links, ppvii–xi It has applications in all fields of social science, as well as in logic, systems science and computer science. Originally, it addressed two-person zero-sum games, in which each participant's gains or losses are exactly balanced by those of other participants. In the 21st century, game theory applies to a wide range of behavioral relations; it is now an umbrella term for the science of logical decision making in humans, animals, as well as computers. Modern game theory began with the idea of mixed-strategy equilibria in two-person zero-sum game and its proof by John von Neumann. Von Neumann's original proof used the Brouwer fixed-point theorem on continuous mappings into compact convex sets, which became a standard method in game theory and mathema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Independent Variable
Dependent and independent variables are variables in mathematical modeling, statistical modeling and experimental sciences. Dependent variables receive this name because, in an experiment, their values are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function), on the values of other variables. Independent variables, in turn, are not seen as depending on any other variable in the scope of the experiment in question. In this sense, some common independent variables are time, space, density, mass, fluid flow rate, and previous values of some observed value of interest (e.g. human population size) to predict future values (the dependent variable). Of the two, it is always the dependent variable whose variation is being studied, by altering inputs, also known as regressors in a statistical context. In an experiment, any variable that can be attributed a value without attributing a value to any other variable is called an ind ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prisoner's Dilemma
The Prisoner's Dilemma is an example of a game analyzed in game theory. It is also a thought experiment that challenges two completely rational agents to a dilemma: cooperate with their partner for mutual reward, or betray their partner ("defect") for individual reward. This dilemma was originally framed by Merrill Flood and Melvin Dresher while working at RAND in 1950. Albert W. Tucker appropriated the game and formalized it by structuring the rewards in terms of prison sentences and named it "prisoner's dilemma". William Poundstone in his 1993 book ''Prisoner's Dilemma'' writes the following version:Two members of a criminal gang are arrested and imprisoned. Each prisoner is in solitary confinement with no means of speaking to or exchanging messages with the other. The police admit they don't have enough evidence to convict the pair on the principal charge. They plan to sentence both to two years in prison on a lesser charge. Simultaneously, the police offer each prisoner a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dominance (game Theory)
In game theory, strategic dominance (commonly called simply dominance) occurs when one strategy is better than another strategy for one player, no matter how that player's opponents may play. Many simple games can be solved using dominance. The opposite, intransitivity, occurs in games where one strategy may be better or worse than another strategy for one player, depending on how the player's opponents may play. Terminology When a player tries to choose the "best" strategy among a multitude of options, that player may compare two strategies A and B to see which one is better. The result of the comparison is one of: * B is equivalent to A: choosing B always gives the same outcome as choosing A, no matter what the other players do. * B strictly dominates A: choosing B always gives a better outcome than choosing A, no matter what the other players do. * B weakly dominates A: choosing B always gives at least as good an outcome as choosing A, no matter what the other players do, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uncorrelated Asymmetry
In game theory an uncorrelated asymmetry is an arbitrary asymmetry in a game which is otherwise symmetrical. The name 'uncorrelated asymmetry' is due to John Maynard Smith who called payoff relevant asymmetries in games with similar roles for each player 'correlated asymmetries' (note that any game with correlated asymmetries must also have uncorrelated asymmetries). The explanation of an uncorrelated asymmetry usually makes reference to "informational asymmetry". Which may confuse some readers, since, games which may have uncorrelated asymmetries are still games of complete information . What differs between the same game with and without an uncorrelated asymmetry is whether the players know which role they have been assigned. If players in a symmetric game know whether they are Player 1, Player 2, ''etc.'' (or row vs. column player in a bimatrix game) then an uncorrelated asymmetry exists. If the players do not know which player they are then no uncorrelated asymmetry exists ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Evolutionarily Stable Strategy
An evolutionarily stable strategy (ESS) is a strategy (or set of strategies) that is ''impermeable'' when adopted by a population in adaptation to a specific environment, that is to say it cannot be displaced by an alternative strategy (or set of strategies) which may be novel or initially rare. Introduced by John Maynard Smith and George R. Price in 1972/3, it is an important concept in behavioural ecology, evolutionary psychology, mathematical game theory and economics, with applications in other fields such as anthropology, philosophy and political science. In game-theoretical terms, an ESS is an equilibrium refinement of the Nash equilibrium, being a Nash equilibrium that is also "evolutionarily stable." Thus, once fixed in a population, natural selection alone is sufficient to prevent alternative (mutant) strategies from replacing it (although this does not preclude the possibility that a better strategy, or set of strategies, will emerge in response to selective pressures r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hawk-dove Game
The game of chicken, also known as the hawk–dove game or snowdrift game, is a model of conflict for two players in game theory. The principle of the game is that while the ideal outcome is for one player to yield (to avoid the worst outcome if neither yields), the individuals try to avoid it out of pride for not wanting to look like a "chicken". Each player taunts the other to increase the risk of shame in yielding. However, when one player yields, the conflict is avoided, and the game is for the most part over. The name "chicken" has its origins in a game in which two drivers drive toward each other on a collision course: one must swerve, or both may die in the crash, but if one driver swerves and the other does not, the one who swerved will be called a "chicken", meaning a coward; this terminology is most prevalent in political science and economics. The name "hawk–dove" refers to a situation in which there is a competition for a shared resource and the contestants can choo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Game Of Chicken
The game of chicken, also known as the hawk–dove game or snowdrift game, is a model of conflict for two players in game theory. The principle of the game is that while the ideal outcome is for one player to yield (to avoid the worst outcome if neither yields), the individuals try to avoid it out of pride for not wanting to look like a "chicken". Each player taunts the other to increase the risk of shame in yielding. However, when one player yields, the conflict is avoided, and the game is for the most part over. The name "chicken" has its origins in a game in which two drivers drive toward each other on a collision course: one must swerve, or both may die in the crash, but if one driver swerves and the other does not, the one who swerved will be called a "chicken", meaning a coward; this terminology is most prevalent in political science and economics. The name "hawk–dove" refers to a situation in which there is a competition for a shared resource and the contestants can choo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
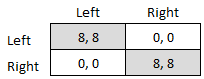
Coordination Game
A coordination game is a type of simultaneous game found in game theory. It describes the situation where a player will earn a higher payoff when they select the same course of action as another player. The game is not one of pure conflict, which results in multiple pure strategy Nash equilibria in which players choose matching strategies. Figure 1 shows a 2-player example. Both (Up, Left) and (Down, Right) are Nash equilibria. If the players expect (Up, Left) to be played, then player 1 thinks their payoff would fall from 2 to 1 if they deviated to Down, and player 2 thinks their payoff would fall from 4 to 3 if they chose Right. If the players expect (Down, Right), player 1 thinks their payoff would fall from 2 to 1 if they deviated to Up, and player 2 thinks their payoff would fall from 4 to 3 if they chose Left. A player's optimal move depends on what they expect the other player to do, and they both do better if they coordinate than if they played an off-equilibrium combinat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
