|
One-way Wave Equation
A one-way wave equation is a first-order partial differential equation describing one wave traveling in a direction defined by the vector wave velocity. It contrasts with the second-order two-way wave equation describing a standing wavefield resulting from superposition of two waves in opposite directions. In the one-dimensional case, the one-way wave equation allows wave propagation to be calculated without the mathematical complication of solving a 2nd order differential equation. Due to the fact that in the last decades no 3D one-way wave equation could be found numerous approximation methods based on the 1D one-way wave equation are used for 3D seismic and other geophysical calculations, see also the section . One-dimensional case The scalar second-order (two-way) wave equation describing a standing wavefield can be written as: \frac - c^2 \frac = 0, where x is the coordinate, t is time, s=s(x,t) is the displacement, and c is the wave velocity. Due to the ambiguity in the d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equation
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a Multivariable calculus, multivariable function. The function is often thought of as an "unknown" to be solved for, similarly to how is thought of as an unknown number to be solved for in an algebraic equation like . However, it is usually impossible to write down explicit formulas for solutions of partial differential equations. There is, correspondingly, a vast amount of modern mathematical and scientific research on methods to Numerical methods for partial differential equations, numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematics, pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Equation
The (two-way) wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields — as they occur in classical physics — such as mechanical waves (e.g. water waves, sound waves and seismic waves) or electromagnetic waves (including light waves). It arises in fields like acoustics, electromagnetism, and fluid dynamics. Single mechanical or electromagnetic waves propagating in a pre-defined direction can also be described with the first-order one-way wave equation which is much easier to solve and also valid for inhomogenious media. Introduction The (two-way) wave equation is a second-order partial differential equation describing waves, including traveling and standing waves; the latter can be considered as linear superpositions of waves traveling in opposite directions. This article mostly focuses on the scalar wave equation describing waves in scalars by scalar functions of a time variable (a variable repres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
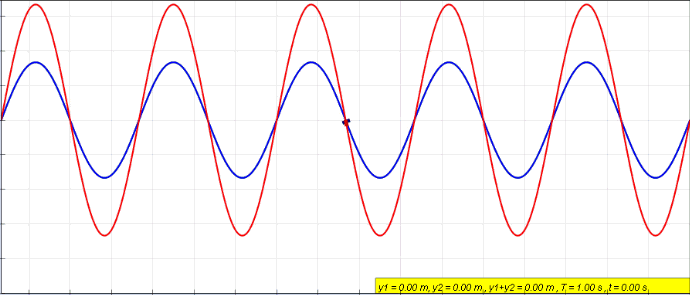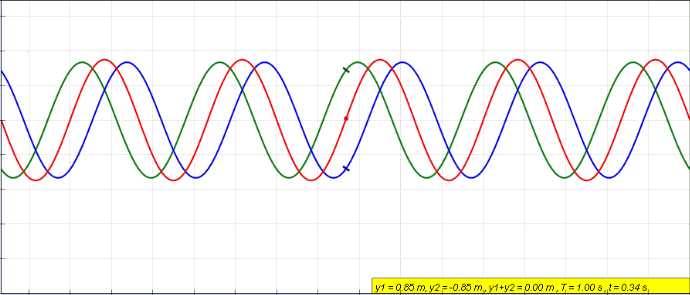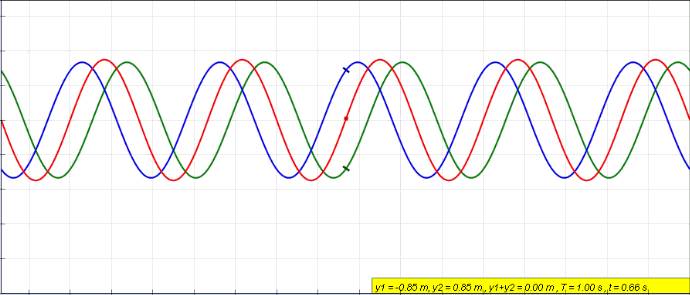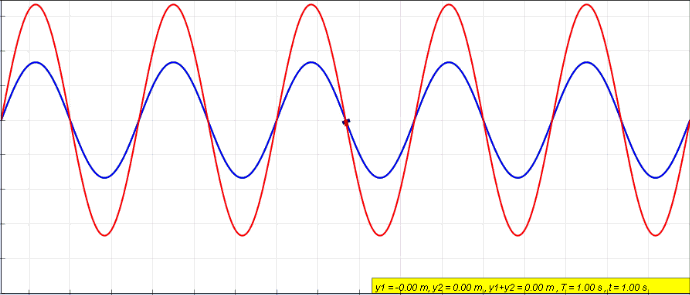
Standing Wave
In physics, a standing wave, also known as a stationary wave, is a wave that oscillates in time but whose peak amplitude profile does not move in space. The peak amplitude of the wave oscillations at any point in space is constant with respect to time, and the oscillations at different points throughout the wave are in phase. The locations at which the absolute value of the amplitude is minimum are called nodes, and the locations where the absolute value of the amplitude is maximum are called antinodes. Standing waves were first noticed by Michael Faraday in 1831. Faraday observed standing waves on the surface of a liquid in a vibrating container. Franz Melde coined the term "standing wave" (German: ''stehende Welle'' or ''Stehwelle'') around 1860 and demonstrated the phenomenon in his classic experiment with vibrating strings. This phenomenon can occur because the medium is moving in the direction opposite to the movement of the wave, or it can arise in a stationary medium ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Factorization
In mathematics, factorization (or factorisation, see American and British English spelling differences#-ise, -ize (-isation, -ization), English spelling differences) or factoring consists of writing a number or another mathematical object as a product of several ''factors'', usually smaller or simpler objects of the same kind. For example, is a factorization of the integer , and is a factorization of the polynomial . Factorization is not usually considered meaningful within number systems possessing division ring, division, such as the real number, real or complex numbers, since any x can be trivially written as (xy)\times(1/y) whenever y is not zero. However, a meaningful factorization for a rational number or a rational function can be obtained by writing it in lowest terms and separately factoring its numerator and denominator. Factorization was first considered by Greek mathematics, ancient Greek mathematicians in the case of integers. They proved the fundamental theorem o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geophysics (journal)
''Geophysics'' is a bimonthly peer-reviewed scientific journal covering all aspects of research, exploration, and education in applied geophysics. It was established in 1936 and is published by the Society of Exploration Geophysicists. The current editor-in-chief is Jeffrey Shragge (Colorado School of Mines). According to the ''Journal Citation Reports'', the journal has a 2018 impact factor of 2.793. See also * List of scientific journals in earth and atmospheric sciences A ''list'' is any set of items in a row. List or lists may also refer to: People * List (surname) Organizations * List College, an undergraduate division of the Jewish Theological Seminary of America * SC Germania List, German rugby unio ... References External links * {{Official website, http://library.seg.org/journal/gpysa7 Geophysics journals English-language journals Publications established in 1936 Academic journals published by learned and professional societies Bimonthly journ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surveys In Geophysics
''Surveys in Geophysics'' is an academic journal published by Springer about geophysics. Its editor-in-chief is Michael Rycroft; its 2019 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a scientometric index calculated by Clarivate that reflects the yearly mean number of citations of articles published in the last two years in a given journal, as ... is 5.544. References Springer Science+Business Media academic journals Geophysics journals {{Geophysics-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elastic Modulus
An elastic modulus (also known as modulus of elasticity) is the unit of measurement of an object's or substance's resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it. The elastic modulus of an object is defined as the slope of its stress–strain curve in the elastic deformation region: A stiffer material will have a higher elastic modulus. An elastic modulus has the form: :\delta \ \stackrel\ \frac where stress is the force causing the deformation divided by the area to which the force is applied and strain is the ratio of the change in some parameter caused by the deformation to the original value of the parameter. Since strain is a dimensionless quantity, the units of \delta will be the same as the units of stress. Specifying how stress and strain are to be measured, including directions, allows for many types of elastic moduli to be defined. The three primary ones are: # ''Young's modulus'' (E) describes tensile and compressive ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stress (mechanics)
In continuum mechanics, stress is a physical quantity. It is a quantity that describes the magnitude of forces that cause deformation. Stress is defined as ''force per unit area''. When an object is pulled apart by a force it will cause elongation which is also known as deformation, like the stretching of an elastic band, it is called tensile stress. But, when the forces result in the compression of an object, it is called compressive stress. It results when forces like tension or compression act on a body. The greater this force and the smaller the cross-sectional area of the body on which it acts, the greater the stress. Therefore, stress is measured in newton per square meter (N/m2) or pascal (Pa). Stress expresses the internal forces that neighbouring particles of a continuous material exert on each other, while strain is the measure of the deformation of the material. For example, when a solid vertical bar is supporting an overhead weight, each particle in the bar pushe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mechanics
Mechanics (from Ancient Greek: μηχανική, ''mēkhanikḗ'', "of machines") is the area of mathematics and physics concerned with the relationships between force, matter, and motion among physical objects. Forces applied to objects result in displacements, or changes of an object's position relative to its environment. Theoretical expositions of this branch of physics has its origins in Ancient Greece, for instance, in the writings of Aristotle and Archimedes (see History of classical mechanics and Timeline of classical mechanics). During the early modern period, scientists such as Galileo, Kepler, Huygens, and Newton laid the foundation for what is now known as classical mechanics. As a branch of classical physics, mechanics deals with bodies that are either at rest or are moving with velocities significantly less than the speed of light. It can also be defined as the physical science that deals with the motion of and forces on bodies not in the quantum realm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deformation (mechanics)
In physics, deformation is the continuum mechanics transformation of a body from a ''reference'' configuration to a ''current'' configuration. A configuration is a set containing the positions of all particles of the body. A deformation can occur because of external loads, intrinsic activity (e.g. muscle contraction), body forces (such as gravity or electromagnetic forces), or changes in temperature, moisture content, or chemical reactions, etc. Strain is related to deformation in terms of ''relative'' displacement of particles in the body that excludes rigid-body motions. Different equivalent choices may be made for the expression of a strain field depending on whether it is defined with respect to the initial or the final configuration of the body and on whether the metric tensor or its dual is considered. In a continuous body, a deformation field results from a stress field due to applied forces or because of some changes in the temperature field of the body. The rel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sound
In physics, sound is a vibration that propagates as an acoustic wave, through a transmission medium such as a gas, liquid or solid. In human physiology and psychology, sound is the ''reception'' of such waves and their ''perception'' by the brain. Only acoustic waves that have frequencies lying between about 20 Hz and 20 kHz, the audio frequency range, elicit an auditory percept in humans. In air at atmospheric pressure, these represent sound waves with wavelengths of to . Sound waves above 20 kHz are known as ultrasound and are not audible to humans. Sound waves below 20 Hz are known as infrasound. Different animal species have varying hearing ranges. Acoustics Acoustics is the interdisciplinary science that deals with the study of mechanical waves in gasses, liquids, and solids including vibration, sound, ultrasound, and infrasound. A scientist who works in the field of acoustics is an ''acoustician'', while someone working in the field of acoustica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bessel Function
Bessel functions, first defined by the mathematician Daniel Bernoulli and then generalized by Friedrich Bessel, are canonical solutions of Bessel's differential equation x^2 \frac + x \frac + \left(x^2 - \alpha^2 \right)y = 0 for an arbitrary complex number \alpha, the ''order'' of the Bessel function. Although \alpha and -\alpha produce the same differential equation, it is conventional to define different Bessel functions for these two values in such a way that the Bessel functions are mostly smooth functions of \alpha. The most important cases are when \alpha is an integer or half-integer. Bessel functions for integer \alpha are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to Laplace's equation in cylindrical coordinates. Spherical Bessel functions with half-integer \alpha are obtained when the Helmholtz equation is solved in spherical coordinates. Applications of Bessel functions The Bessel function is a generalizat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
