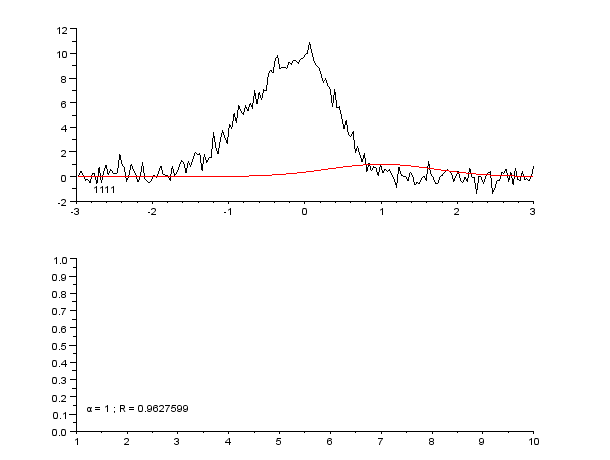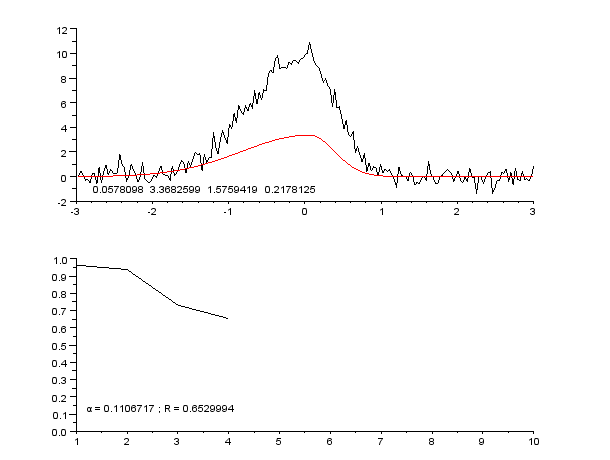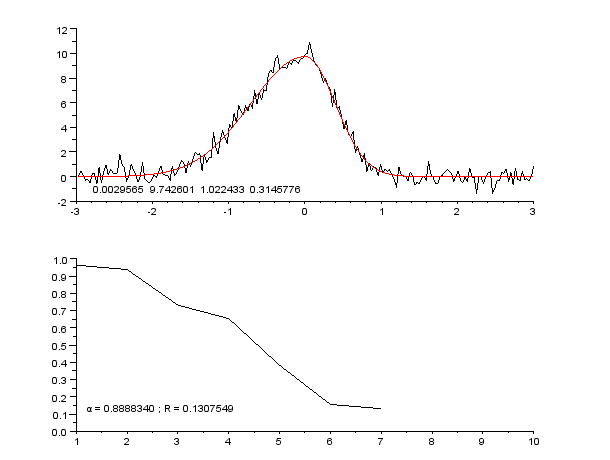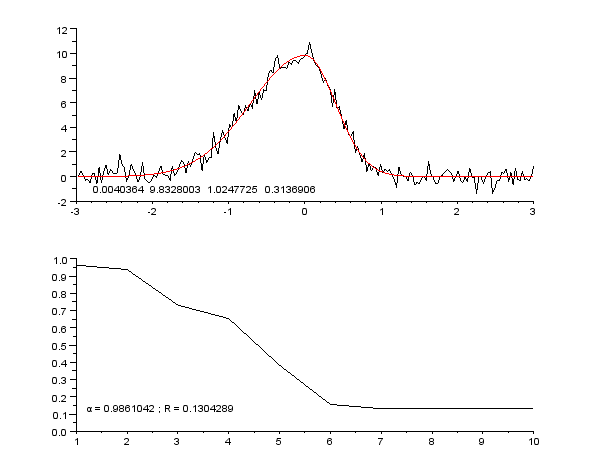
|
Normal Distance
In geometry, the perpendicular distance between two objects is the distance from one to the other, measured along a line that is perpendicular to one or both. The distance from a point to a line is the distance to the nearest point on that line. That is the point at which a segment from it to the given point is perpendicular to the line. Likewise, the distance from a point to a curve is measured by a line segment that is perpendicular to a tangent line to the curve at the nearest point on the curve. The distance from a point to a plane is measured as the length from the point along a segment that is perpendicular to the plane, meaning that it is perpendicular to all lines in the plane that pass through the nearest point in the plane to the given point. Other instances include: *'' Point on plane closest to origin'', for the perpendicular distance from the origin to a plane in three-dimensional space *'' Nearest distance between skew lines'', for the perpendicular distance between ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projection (linear Algebra)
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself (an endomorphism) such that P\circ P=P. That is, whenever P is applied twice to any vector, it gives the same result as if it were applied once (i.e. P is idempotent). It leaves its image unchanged. This definition of "projection" formalizes and generalizes the idea of graphical projection. One can also consider the effect of a projection on a geometrical object by examining the effect of the projection on points in the object. Definitions A projection on a vector space V is a linear operator P : V \to V such that P^2 = P. When V has an inner product and is complete (i.e. when V is a Hilbert space) the concept of orthogonality can be used. A projection P on a Hilbert space V is called an orthogonal projection if it satisfies \langle P \mathbf x, \mathbf y \rangle = \langle \mathbf x, P \mathbf y \rangle for all \mathbf x, \mathbf y \in V. A projection on a Hilbe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signed Distance
In mathematics and its applications, the signed distance function (or oriented distance function) is the orthogonal distance of a given point ''x'' to the boundary of a set Ω in a metric space, with the sign determined by whether or not ''x'' is in the interior of Ω. The function has positive values at points ''x'' inside Ω, it decreases in value as ''x'' approaches the boundary of Ω where the signed distance function is zero, and it takes negative values outside of Ω. However, the alternative convention is also sometimes taken instead (i.e., negative inside Ω and positive outside). Definition If Ω is a subset of a metric space ''X'' with metric ''d'', then the ''signed distance function'' ''f'' is defined by :f(x) = \begin d(x, \partial \Omega) & \mbox\, x \in \Omega \\ -d(x, \partial \Omega) & \mbox\, x \in \Omega^c \end where \partial \Omega denotes the boundary of For any : d(x, \partial \Omega) := \inf_d(x, y) where denotes the infimum. Properties in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moment Of Inertia
The moment of inertia, otherwise known as the mass moment of inertia, angular mass, second moment of mass, or most accurately, rotational inertia, of a rigid body is a quantity that determines the torque needed for a desired angular acceleration about a rotational axis, akin to how mass determines the force needed for a desired acceleration. It depends on the body's mass distribution and the axis chosen, with larger moments requiring more torque to change the body's rate of rotation. It is an extensive (additive) property: for a point mass the moment of inertia is simply the mass times the square of the perpendicular distance to the axis of rotation. The moment of inertia of a rigid composite system is the sum of the moments of inertia of its component subsystems (all taken about the same axis). Its simplest definition is the second moment of mass with respect to distance from an axis. For bodies constrained to rotate in a plane, only their moment of inertia about an ax ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypercycle (geometry)
In hyperbolic geometry, a hypercycle, hypercircle or equidistant curve is a curve whose points have the same orthogonal distance from a given straight line (its axis). Given a straight line and a point not on , one can construct a hypercycle by taking all points on the same side of as , with perpendicular distance to equal to that of . The line is called the ''axis'', ''center'', or ''base line'' of the hypercycle. The lines perpendicular to , which are also perpendicular to the hypercycle, are called the ''normals'' of the hypercycle. The segments of the normals between and the hypercycle are called the ''radii''. Their common length is called the ''distance'' or ''radius'' of the hypercycle. The hypercycles through a given point that share a tangent through that point converge towards a horocycle as their distances go towards infinity. Properties similar to those of Euclidean lines Hypercycles in hyperbolic geometry have some properties similar to those of lines in E ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Distance Between Sets
Distance is a numerical or occasionally qualitative measurement of how far apart objects or points are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria (e.g. "two counties over"). Since spatial cognition is a rich source of conceptual metaphors in human thought, the term is also frequently used metaphorically to mean a measurement of the amount of difference between two similar objects (such as statistical distance between probability distributions or edit distance between strings of text) or a degree of separation (as exemplified by distance between people in a social network). Most such notions of distance, both physical and metaphorical, are formalized in mathematics using the notion of a metric space. In the social sciences, distance can refer to a qualitative measurement of separation, such as social distance or psychological distance. Distances in physics and geometry The distance between physical l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Offset Surface
A parallel of a curve is the envelope of a family of congruent circles centered on the curve. It generalises the concept of '' parallel (straight) lines''. It can also be defined as a curve whose points are at a constant '' normal distance'' from a given curve. These two definitions are not entirely equivalent as the latter assumes smoothness, whereas the former does not. In computer-aided design the preferred term for a parallel curve is offset curve. (In other geometric contexts, the term offset can also refer to translation.) Offset curves are important for example in numerically controlled machining, where they describe for example the shape of the cut made by a round cutting tool of a two-axis machine. The shape of the cut is offset from the trajectory of the cutter by a constant distance in the direction normal to the cutter trajectory at every point. In the area of 2D computer graphics known as vector graphics, the (approximate) computation of parallel curves is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Fitting
Curve fitting is the process of constructing a curve, or mathematical function, that has the best fit to a series of data points, possibly subject to constraints. Curve fitting can involve either interpolation, where an exact fit to the data is required, or smoothing, in which a "smooth" function is constructed that approximately fits the data. A related topic is regression analysis, which focuses more on questions of statistical inference such as how much uncertainty is present in a curve that is fit to data observed with random errors. Fitted curves can be used as an aid for data visualization, to infer values of a function where no data are available, and to summarize the relationships among two or more variables. Extrapolation refers to the use of a fitted curve beyond the range of the observed data, and is subject to a degree of uncertainty since it may reflect the method used to construct the curve as much as it reflects the observed data. For linear-algebraic analysis of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Foot Of A Normal
In geometry, a normal is an object such as a line, ray, or vector that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the (infinite) line perpendicular to the tangent line to the curve at the point. A normal vector may have length one (a unit vector) or its length may represent the curvature of the object (a '' curvature vector''); its algebraic sign may indicate sides (interior or exterior). In three dimensions, a surface normal, or simply normal, to a surface at point P is a vector perpendicular to the tangent plane of the surface at P. The word "normal" is also used as an adjective: a line ''normal'' to a plane, the ''normal'' component of a force, the normal vector, etc. The concept of normality generalizes to orthogonality ( right angles). The concept has been generalized to differentiable manifolds of arbitrary dimension embedded in a Euclidean space. The normal vector space or normal space of a manifold at p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Normal
In geometry, a normal is an object such as a line, ray, or vector that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the (infinite) line perpendicular to the tangent line to the curve at the point. A normal vector may have length one (a unit vector) or its length may represent the curvature of the object (a '' curvature vector''); its algebraic sign may indicate sides (interior or exterior). In three dimensions, a surface normal, or simply normal, to a surface at point P is a vector perpendicular to the tangent plane of the surface at P. The word "normal" is also used as an adjective: a line ''normal'' to a plane, the ''normal'' component of a force, the normal vector, etc. The concept of normality generalizes to orthogonality (right angles). The concept has been generalized to differentiable manifolds of arbitrary dimension embedded in a Euclidean space. The normal vector space or normal space of a manifold at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Principal Components Analysis
Principal component analysis (PCA) is a popular technique for analyzing large datasets containing a high number of dimensions/features per observation, increasing the interpretability of data while preserving the maximum amount of information, and enabling the visualization of multidimensional data. Formally, PCA is a statistical technique for reducing the dimensionality of a dataset. This is accomplished by linearly transforming the data into a new coordinate system where (most of) the variation in the data can be described with fewer dimensions than the initial data. Many studies use the first two principal components in order to plot the data in two dimensions and to visually identify clusters of closely related data points. Principal component analysis has applications in many fields such as population genetics, microbiome studies, and atmospheric science. The principal components of a collection of points in a real coordinate space are a sequence of p unit vectors, where t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonal (mathematics)
In mathematics, orthogonality is the generalization of the geometric notion of '' perpendicularity'' to the linear algebra of bilinear forms. Two elements ''u'' and ''v'' of a vector space with bilinear form ''B'' are orthogonal when . Depending on the bilinear form, the vector space may contain nonzero self-orthogonal vectors. In the case of function spaces, families of orthogonal functions are used to form a basis. The concept has been used in the context of orthogonal functions, orthogonal polynomials, and combinatorics. Definitions * In geometry, two Euclidean vectors are orthogonal if they are perpendicular, ''i.e.'', they form a right angle. * Two vectors, ''x'' and ''y'', in an inner product space, ''V'', are ''orthogonal'' if their inner product \langle x, y \rangle is zero. This relationship is denoted x \perp y. *An orthogonal matrix is a matrix whose column vectors are orthonormal to each other. * Two vector subspaces, ''A'' and ''B'', of an inner product space ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |