|
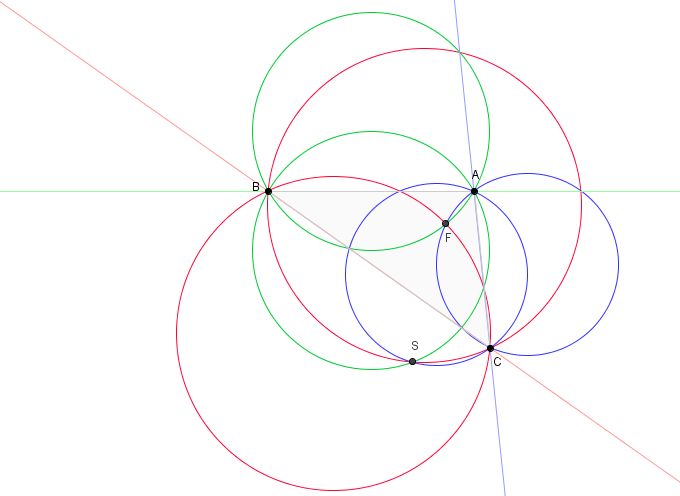
Nine-point Hyperbola
In Euclidean geometry with triangle , the nine-point hyperbola is an instance of the nine-point conic described by American mathematician Maxime Bôcher in 1892. The celebrated nine-point circle is a separate instance of Bôcher's conic: :Given a triangle and a point in its plane, a conic can be drawn through the following nine points: :: the midpoints of the sides of , :: the midpoints of the lines joining to the vertices, and :: the points where these last named lines cut the sides of the triangle. The conic is an ellipse if lies in the interior of or in one of the regions of the plane separated from the interior by two sides of the triangle; otherwise, the conic is a hyperbola. Bôcher notes that when is the orthocenter, one obtains the nine-point circle, and when is on the circumcircle of , then the conic is an equilateral hyperbola. Allen An approach to the nine-point hyperbola using the analytic geometry of split-complex numbers was devised by E. F. Allen in 194 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nine Point Conic
9 is a number, numeral, and glyph. 9 or nine may also refer to: Dates * AD 9, the ninth year of the AD era * 9 BC, the ninth year before the AD era * 9, numerical symbol for the month of September Places * Nine, Portugal, a parish in the town of Vila Nova de Famalicão * Planet Nine, a planet proposed to exist in the outer Solar System * Zheleznogorsk, Krasnoyarsk Krai, Russia, a closed town * The 9, a residential portion of Ameritrust Tower in Cleveland People * Louis Niñé (1922–1983), a New York politician whose surname is usually rendered "Nine" * Nine (rapper) (born 1969), a hip hop musician * Tech N9ne (born 1971), an American rapper Fictional characters * The Nine, epithet for the Nazgûl in J. R. R. Tolkien's Middle-earth legendarium * ⑨, a derogatory name for Cirno, an ice fairy from the dōjin game ''Touhou Project'' Literature * ''The Nine (book)'', a 2007 book by Jeffrey Toobin * ''NiNe. magazine'', a magazine for teenage girls * ''Nine'' (manga), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Euclidean plane. In topology, it is often denoted as because it is a one-dimensional unit -sphere. If is a point on the unit circle's circumference, then and are the lengths of the legs of a right triangle whose hypotenuse has length 1. Thus, by the Pythagorean theorem, and satisfy the equation x^2 + y^2 = 1. Since for all , and since the reflection of any point on the unit circle about the - or -axis is also on the unit circle, the above equation holds for all points on the unit circle, not only those in the first quadrant. The interior of the unit circle is called the open unit disk, while the interior of the unit circle combined with the unit circle itself is called the closed unit disk. One may also use other notions of "dista ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Excenter
In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches (is tangent to) the three sides. The center of the incircle is a triangle center called the triangle's incenter. An excircle or escribed circle of the triangle is a circle lying outside the triangle, tangent to one of its sides and tangent to the extensions of the other two. Every triangle has three distinct excircles, each tangent to one of the triangle's sides. The center of the incircle, called the incenter, can be found as the intersection of the three internal angle bisectors. The center of an excircle is the intersection of the internal bisector of one angle (at vertex , for example) and the external bisectors of the other two. The center of this excircle is called the excenter relative to the vertex , or the excenter of . Because the internal bisector of an angle is perpendicular to its external bisector, it follows that the center of the in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Incenter
In geometry, the incenter of a triangle is a triangle center, a point defined for any triangle in a way that is independent of the triangle's placement or scale. The incenter may be equivalently defined as the point where the internal angle bisectors of the triangle cross, as the point equidistant from the triangle's sides, as the junction point of the medial axis and innermost point of the grassfire transform of the triangle, and as the center point of the inscribed circle of the triangle. Together with the centroid, circumcenter, and orthocenter, it is one of the four triangle centers known to the ancient Greeks, and the only one of the four that does not in general lie on the Euler line. It is the first listed center, X(1), in Clark Kimberling's Encyclopedia of Triangle Centers, and the identity element of the multiplicative group of triangle centers.. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kiepert Conics
In triangle geometry, the Kiepert conics are two special conics associated with the reference triangle. One of them is a hyperbola, called the Kiepert hyperbola and the other is a parabola, called the Kiepert parabola. The Kiepert conics are defined as follows: :If the three triangles A^\prime BC, AB^\prime C and ABC^\prime, constructed on the sides of a triangle ABC as bases, are similar, isosceles and similarly situated, then the triangles ABC and A^\prime B^\prime C^\prime are in perspective. As the base angle of the isosceles triangles varies between -\pi/2 and \pi/2, the locus of the center of perspectivity of the triangles ABC and A^\prime B^\prime C^\prime is a hyperbola called the Kiepert hyperbola and the envelope of their axis of perspectivity is a parabola called the Kiepert parabola. It has been proved that the Kiepert hyperbola is the hyperbola passing through the vertices, the centroid and the orthocenter of the reference triangle and the Kiepert parabola is the pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Encyclopedia Of Triangle Centers
The Encyclopedia of Triangle Centers (ETC) is an online list of thousands of points or "centers" associated with the geometry of a triangle. It is maintained by Clark Kimberling, Professor of Mathematics at the University of Evansville. , the list identifies 52,440 triangle centers. Each point in the list is identified by an index number of the form ''X''(''n'')—for example, ''X''(1) is the incenter. The information recorded about each point includes its trilinear and barycentric coordinates and its relation to lines joining other identified points. Links to The Geometer's Sketchpad diagrams are provided for key points. The Encyclopedia also includes a glossary of terms and definitions. Each point in the list is assigned a unique name. In cases where no particular name arises from geometrical or historical considerations, the name of a star is used instead. For example, the 770th point in the list is named ''point Acamar''. The first 10 points listed in the Encyclopedia ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Napoleon Points
In geometry, Napoleon points are a pair of special points associated with a plane triangle. It is generally believed that the existence of these points was discovered by Napoleon Bonaparte, the Emperor of the French from 1804 to 1815, but many have questioned this belief. The Napoleon points are triangle centers and they are listed as the points X(17) and X(18) in Clark Kimberling's Encyclopedia of Triangle Centers. The name "Napoleon points" has also been applied to a different pair of triangle centers, better known as the isodynamic points. Definition of the points First Napoleon point Let ''ABC'' be any given plane triangle. On the sides ''BC'', ''CA'', ''AB'' of the triangle, construct outwardly drawn equilateral triangles ''DBC'', ''ECA'' and ''FAB'' respectively. Let the centroids of these triangles be ''X'', ''Y'' and ''Z'' respectively. Then the lines ''AX'', ''BY'' and ''CZ'' are concurrent. The point of concurrence ''N1'' is the first Napoleon point, or the outer Nap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermat Point
In Euclidean geometry, the Fermat point of a triangle, also called the Torricelli point or Fermat–Torricelli point, is a point such that the sum of the three distances from each of the three vertices of the triangle to the point is the smallest possible. It is so named because this problem was first raised by Fermat in a private letter to Evangelista Torricelli, who solved it. The Fermat point gives a solution to the geometric median and Steiner tree problems for three points. Construction The Fermat point of a triangle with largest angle at most 120° is simply its first isogonic center or X(13), which is constructed as follows: # Construct an equilateral triangle on each of two arbitrarily chosen sides of the given triangle. # Draw a line from each new vertex to the opposite vertex of the original triangle. # The two lines intersect at the Fermat point. An alternative method is the following: # On each of two arbitrarily chosen sides, construct an isosceles triangle, with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Centroid
In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the surface of the figure. The same definition extends to any object in ''n''-dimensional Euclidean space. In geometry, one often assumes uniform mass density, in which case the ''barycenter'' or ''center of mass'' coincides with the centroid. Informally, it can be understood as the point at which a cutout of the shape (with uniformly distributed mass) could be perfectly balanced on the tip of a pin. In physics, if variations in gravity are considered, then a ''center of gravity'' can be defined as the weighted mean of all points weighted by their specific weight. In geography, the centroid of a radial projection of a region of the Earth's surface to sea level is the region's geographical center. History The term "centroid" is of recent coinage (1814). It is used as a substitute for the older te ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Hyperbola
In geometry, the unit hyperbola is the set of points (''x'',''y'') in the Cartesian plane that satisfy the implicit equation x^2 - y^2 = 1 . In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an ''alternative radial length'' : r = \sqrt . Whereas the unit circle surrounds its center, the unit hyperbola requires the ''conjugate hyperbola'' y^2 - x^2 = 1 to complement it in the plane. This pair of hyperbolas share the asymptotes ''y'' = ''x'' and ''y'' = −''x''. When the conjugate of the unit hyperbola is in use, the alternative radial length is r = \sqrt . The unit hyperbola is a special case of the rectangular hyperbola, with a particular orientation, location, and scale. As such, its eccentricity equals \sqrt. The unit hyperbola finds applications where the circle must be replaced with the hyperbola for purposes of analytic geometry. A prominent instance is the depiction of spacetime as a pseudo-Euclidean space. There the asymptotes of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Mathematical Gazette
''The Mathematical Gazette'' is an academic journal of mathematics education, published three times yearly, that publishes "articles about the teaching and learning of mathematics with a focus on the 15–20 age range and expositions of attractive areas of mathematics." It was established in 1894 by Edward Mann Langley as the successor to the Reports of the Association for the Improvement of Geometrical Teaching. Its publisher is the Mathematical Association. William John Greenstreet was its editor for more than thirty years (1897–1930). Since 2000, the editor is Gerry Leversha. Editors * Edward Mann Langley: 1894-1896 * Francis Sowerby Macaulay: 1896-1897 * William John Greenstreet: 1897-1930 * Alan Broadbent: 1930-1955 * Reuben Goodstein: 1956-1962 * Edwin A. Maxwell: 1962-1971 * Douglas Quadling Douglas Arthur Quadling (1926–2015) was an English mathematician, school master and educationalist who was one of the four drivers behind the School Mathematics Project (SMP) i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Incircle And Excircles Of A Triangle
In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches (is tangent to) the three sides. The center of the incircle is a triangle center called the triangle's incenter. An excircle or escribed circle of the triangle is a circle lying outside the triangle, tangent to one of its sides and tangent to the extensions of the other two. Every triangle has three distinct excircles, each tangent to one of the triangle's sides. The center of the incircle, called the incenter, can be found as the intersection of the three internal angle bisectors. The center of an excircle is the intersection of the internal bisector of one angle (at vertex , for example) and the external bisectors of the other two. The center of this excircle is called the excenter relative to the vertex , or the excenter of . Because the internal bisector of an angle is perpendicular to its external bisector, it follows that the center of the in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |