|
Neural Network Quantum States
Neural Network Quantum States (NQS or NNQS) is a general class of Variational method (quantum mechanics), variational quantum states parameterized in terms of an artificial neural network. It was first introduced in 2017 by the physicists Giuseppe Carleo and Matthias Troyer to approximate wave functions of many-body quantum systems. Given a many-body quantum state , \Psi\rangle comprising N degrees of freedom and a choice of associated quantum numbers s_1 \ldots s_N , then an NQS parameterizes the wave-function amplitudes \langle s_1 \ldots s_N , \Psi; W \rangle = F(s_1 \ldots s_N; W), where F(s_1 \ldots s_N; W) is an artificial neural network of parameters (weights) W , N input variables ( s_1 \ldots s_N ) and one complex-valued output corresponding to the wave-function amplitude. This variational form is used in conjunction with specific stochastic learning approaches to approximate quantum states of interest. Learning the Ground-State Wave Function One common app ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Variational Method (quantum Mechanics)
In quantum mechanics, the variational method is one way of finding approximations to the lowest energy eigenstate or ground state, and some excited states. This allows calculating approximate wavefunctions such as molecular orbitals. The basis for this method is the variational principle. The method consists of choosing a "trial wavefunction" depending on one or more parameters, and finding the values of these parameters for which the expectation value of the energy is the lowest possible. The wavefunction obtained by fixing the parameters to such values is then an approximation to the ground state wavefunction, and the expectation value of the energy in that state is an upper bound to the ground state energy. The Hartree–Fock method, density matrix renormalization group, and Ritz method apply the variational method. Description Suppose we are given a Hilbert space and a Hermitian operator over it called the Hamiltonian H . Ignoring complications about continuous spectr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Variational Monte Carlo
In computational physics, variational Monte Carlo (VMC) is a quantum Monte Carlo method that applies the Variational method (quantum mechanics), variational method to approximate the ground state of a quantum system. The basic building block is a generic wave function , \Psi(a) \rangle depending on some parameters a . The optimal values of the parameters a is then found upon minimizing the total energy of the system. In particular, given the Hamiltonian (quantum mechanics), Hamiltonian \mathcal , and denoting with X a Many-body problem, many-body configuration, the expectation value of the energy can be written as: E(a) = \frac = \frac . Following the Monte Carlo method for evaluating integrals, we can interpret \frac as a probability distribution function, sample it, and evaluate the energy expectation value E(a) as the average of the so-called local energy E_(X) = \frac . Once E(a) is known for a given set of variational parameters a , then optimization is pe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Quantum States
In quantum physics, a quantum state is a mathematical entity that embodies the knowledge of a quantum system. Quantum mechanics specifies the construction, evolution, and measurement of a quantum state. The result is a prediction for the system represented by the state. Knowledge of the quantum state, and the rules for the system's evolution in time, exhausts all that can be known about a quantum system. Quantum states may be defined differently for different kinds of systems or problems. Two broad categories are * wave functions describing quantum systems using position or momentum variables and * the more abstract vector quantum states. Historical, educational, and application-focused problems typically feature wave functions; modern professional physics uses the abstract vector states. In both categories, quantum states divide into pure versus mixed states, or into coherent states and incoherent states. Categories with special properties include stationary states for time ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Differentiable Programming
Differentiable programming is a programming paradigm in which a numeric computer program can be differentiated throughout via automatic differentiation. This allows for gradient-based optimization of parameters in the program, often via gradient descent, as well as other learning approaches that are based on higher-order derivative information. Differentiable programming has found use in a wide variety of areas, particularly scientific computing and machine learning. One of the early proposals to adopt such a framework in a systematic fashion to improve upon learning algorithms was made by the Advanced Concepts Team at the European Space Agency in early 2016. Approaches Most differentiable programming frameworks work by constructing a graph containing the control flow and data structures in the program. Attempts generally fall into two groups: * Static, compiled graph-based approaches such as TensorFlow,TensorFlow 1 uses the static graph approach, whereas TensorFlow 2 uses the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Entropy Of Entanglement
The entropy of entanglement (or entanglement entropy) is a measure of the degree of quantum entanglement between two subsystems constituting a two-part composite quantum system. Given a pure bipartite quantum state of the composite system, it is possible to obtain a reduced density matrix describing knowledge of the state of a subsystem. The entropy of entanglement is the Von Neumann entropy of the reduced density matrix for any of the subsystems. If it is non-zero, it indicates the two subsystems are entangled. More mathematically; if a state describing two subsystems ''A'' and ''B'' , \Psi_\rangle=, \phi_A\rangle, \phi_B\rangle is a separable state, then the reduced density matrix \rho_A=\operatorname_B, \Psi_\rangle\langle\Psi_, =, \phi_A\rangle\langle\phi_A, is a pure state. Thus, the entropy of the state is zero. Similarly, the density matrix of ''B'' would also have 0 entropy. A reduced density matrix having a non-zero entropy is therefore a signal of the existence of e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Matrix Product State
A matrix product state (MPS) is a representation of a quantum many-body state. It is at the core of one of the most effective algorithms for solving one dimensional strongly correlated quantum systems – the density matrix renormalization group (DMRG) algorithm. For a system of N spins of dimension d, the general form of the MPS for periodic boundary conditions (PBC) can be written in the following form: , \Psi\rangle = \sum_ \operatorname\left[A_1^ A_2^ \cdots A_N^\right] , s_1 s_2 \ldots s_N\rangle. For open boundary conditions (OBC), , \Psi\rangle takes the form , \Psi\rangle = \sum_ A_1^ A_2^ \cdots A_N^ , s_1 s_2 \ldots s_N\rangle. Here A_i^ are the D_i\times D_ matrices (D is the dimension of the virtual subsystems) and , s_i\rangle are the single-site basis states. For periodic boundary conditions, we consider D_=D_1, and for open boundary conditions D_1=1. The parameter D is related to the Quantum entanglement, entanglement between particles. In particular, if ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Tensor Networks
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects associated with a vector space. Tensors may map between different objects such as vectors, scalars, and even other tensors. There are many types of tensors, including scalars and vectors (which are the simplest tensors), dual vectors, multilinear maps between vector spaces, and even some operations such as the dot product. Tensors are defined independent of any basis, although they are often referred to by their components in a basis related to a particular coordinate system; those components form an array, which can be thought of as a high-dimensional matrix. Tensors have become important in physics because they provide a concise mathematical framework for formulating and solving physics problems in areas such as mechanics ( stress, elasticity, quantum mechanics, fluid mechanics, moment of inertia, ...), electrodynamics (electromagnetic tensor, Maxw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
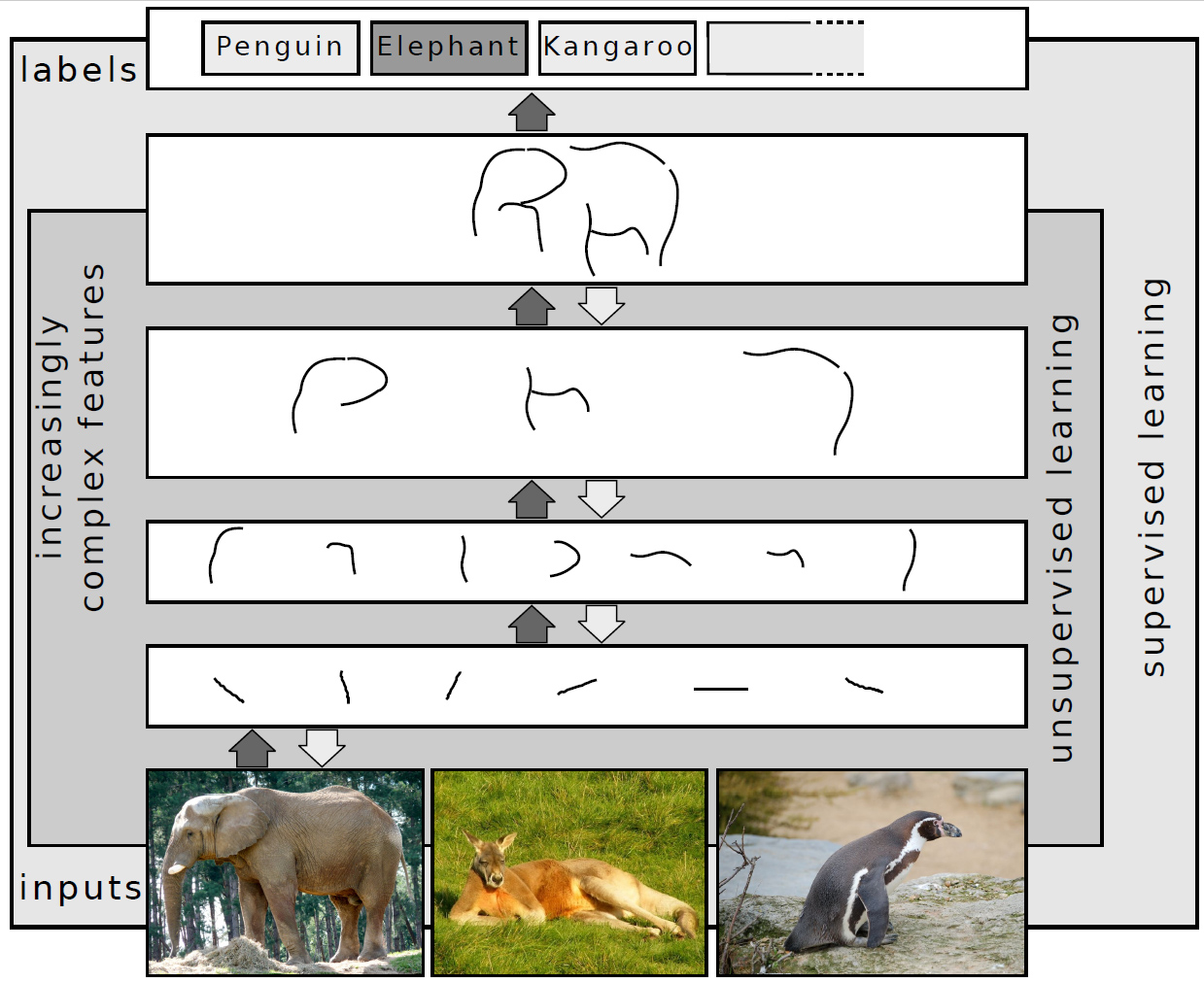
Unsupervised Learning
Unsupervised learning is a framework in machine learning where, in contrast to supervised learning, algorithms learn patterns exclusively from unlabeled data. Other frameworks in the spectrum of supervisions include weak- or semi-supervision, where a small portion of the data is tagged, and self-supervision. Some researchers consider self-supervised learning a form of unsupervised learning. Conceptually, unsupervised learning divides into the aspects of data, training, algorithm, and downstream applications. Typically, the dataset is harvested cheaply "in the wild", such as massive text corpus obtained by web crawling, with only minor filtering (such as Common Crawl). This compares favorably to supervised learning, where the dataset (such as the ImageNet1000) is typically constructed manually, which is much more expensive. There were algorithms designed specifically for unsupervised learning, such as clustering algorithms like k-means, dimensionality reduction techniques l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
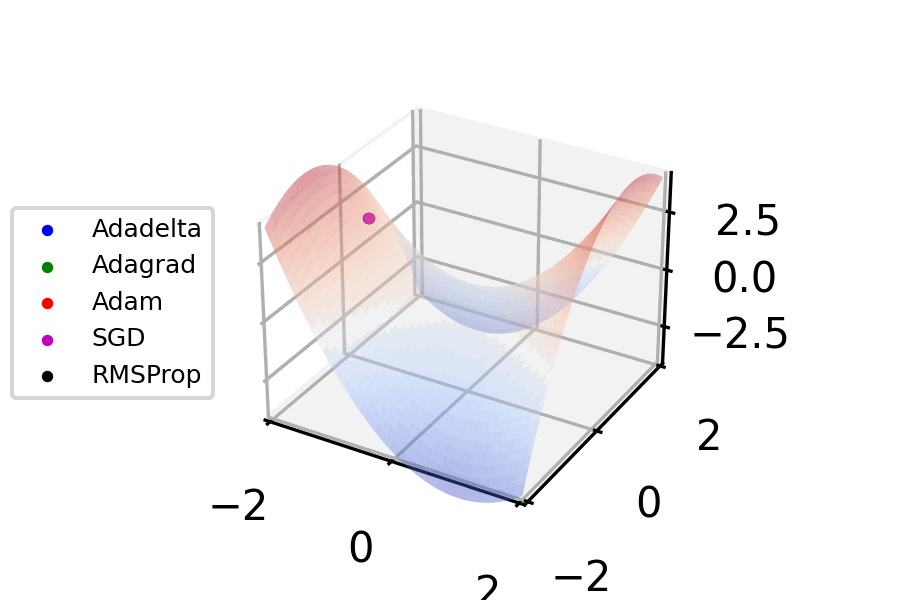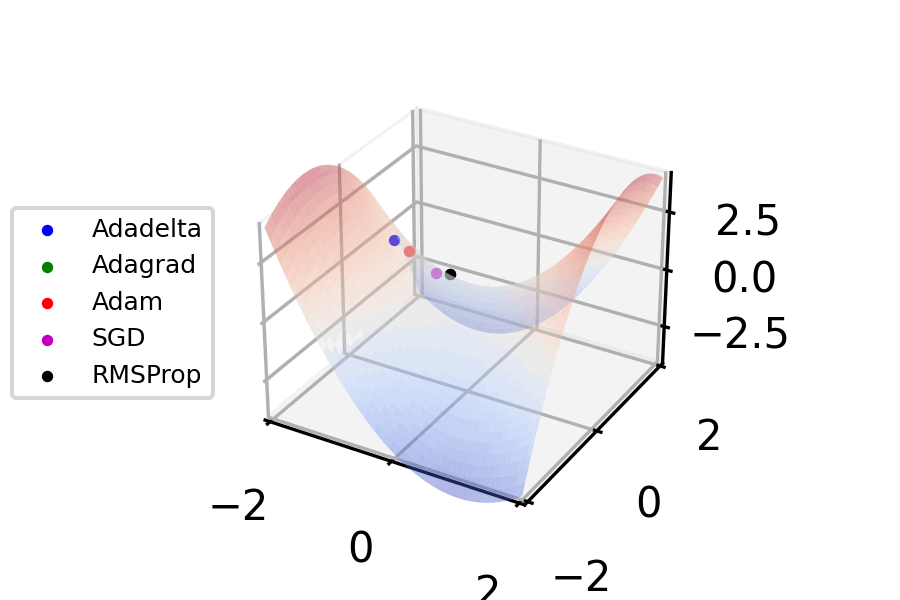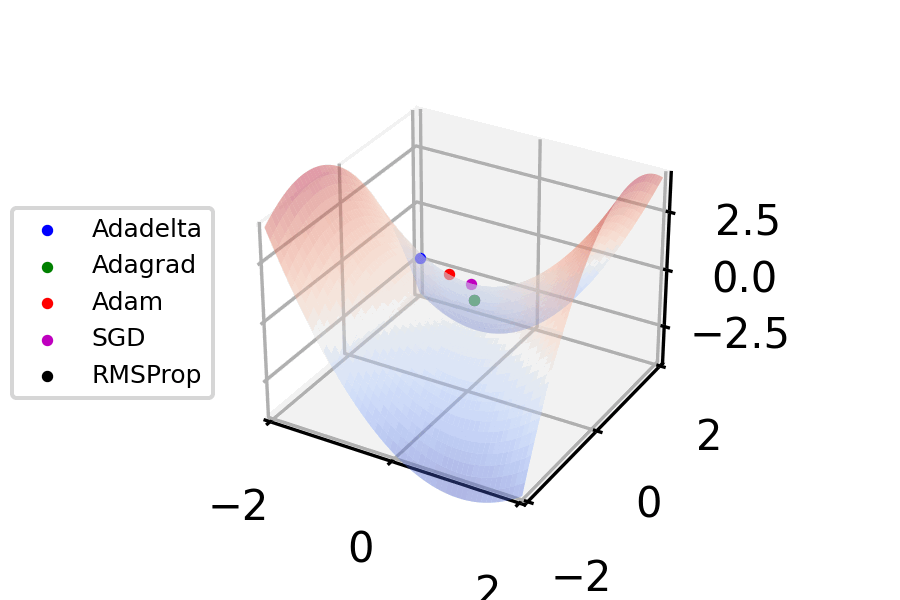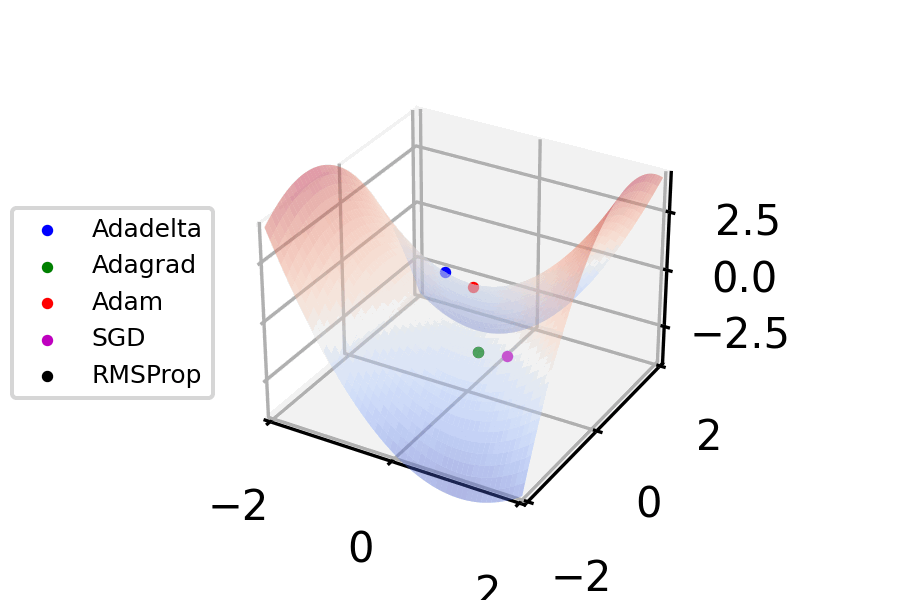
Stochastic Gradient Descent
Stochastic gradient descent (often abbreviated SGD) is an Iterative method, iterative method for optimizing an objective function with suitable smoothness properties (e.g. Differentiable function, differentiable or Subderivative, subdifferentiable). It can be regarded as a stochastic approximation of gradient descent optimization, since it replaces the actual gradient (calculated from the entire data set) by an estimate thereof (calculated from a randomly selected subset of the data). Especially in high-dimensional optimization problems this reduces the very high Computational complexity, computational burden, achieving faster iterations in exchange for a lower Rate of convergence, convergence rate. The basic idea behind stochastic approximation can be traced back to the Robbins–Monro algorithm of the 1950s. Today, stochastic gradient descent has become an important optimization method in machine learning. Background Both statistics, statistical M-estimation, estimation and ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Backpropagation
In machine learning, backpropagation is a gradient computation method commonly used for training a neural network to compute its parameter updates. It is an efficient application of the chain rule to neural networks. Backpropagation computes the gradient of a loss function with respect to the weights of the network for a single input–output example, and does so efficiently, computing the gradient one layer at a time, iterating backward from the last layer to avoid redundant calculations of intermediate terms in the chain rule; this can be derived through dynamic programming. Strictly speaking, the term ''backpropagation'' refers only to an algorithm for efficiently computing the gradient, not how the gradient is used; but the term is often used loosely to refer to the entire learning algorithm – including how the gradient is used, such as by stochastic gradient descent, or as an intermediate step in a more complicated optimizer, such as Adaptive Moment Estimation. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Deep Learning
Deep learning is a subset of machine learning that focuses on utilizing multilayered neural networks to perform tasks such as classification, regression, and representation learning. The field takes inspiration from biological neuroscience and is centered around stacking artificial neurons into layers and "training" them to process data. The adjective "deep" refers to the use of multiple layers (ranging from three to several hundred or thousands) in the network. Methods used can be either supervised, semi-supervised or unsupervised. Some common deep learning network architectures include fully connected networks, deep belief networks, recurrent neural networks, convolutional neural networks, generative adversarial networks, transformers, and neural radiance fields. These architectures have been applied to fields including computer vision, speech recognition, natural language processing, machine translation, bioinformatics, drug design, medical image analysis, c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Gradient
In vector calculus, the gradient of a scalar-valued differentiable function f of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p gives the direction and the rate of fastest increase. The gradient transforms like a vector under change of basis of the space of variables of f. If the gradient of a function is non-zero at a point p, the direction of the gradient is the direction in which the function increases most quickly from p, and the magnitude of the gradient is the rate of increase in that direction, the greatest absolute directional derivative. Further, a point where the gradient is the zero vector is known as a stationary point. The gradient thus plays a fundamental role in optimization theory, where it is used to minimize a function by gradient descent. In coordinate-free terms, the gradient of a function f(\mathbf) may be defined by: df=\nabla f \cdot d\mathbf where df is the total infinitesimal change in f for a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |