|
Nephroid
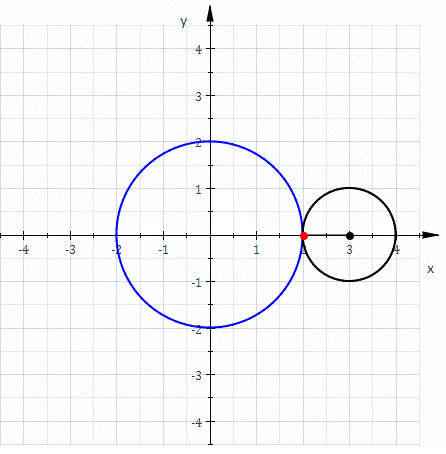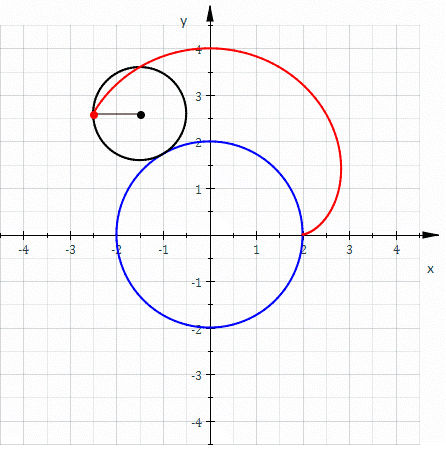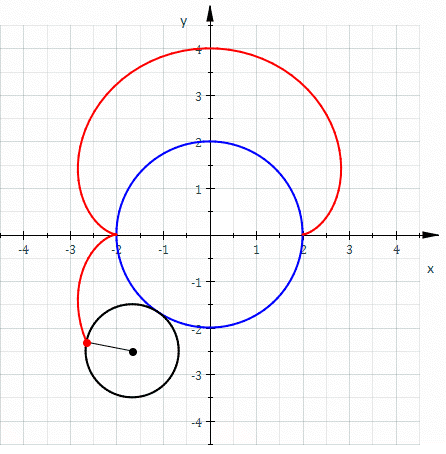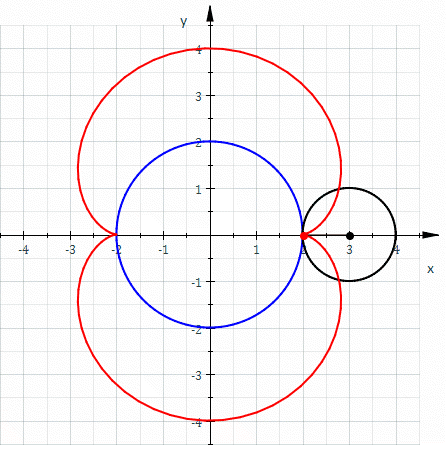
In geometry, a nephroid () is a specific plane curve. It is a type of epicycloid in which the smaller circle's radius differs from the larger by a factor of one-half. Name Although the term ''nephroid'' was used to describe other curves, it was applied to the curve in this article by Richard A. Proctor in 1878. Strict definition A nephroid is * an algebraic curve of degree 6. * an epicycloid with two cusps * a plane simple closed curve = a Jordan curve Equations Parametric If the small circle has radius a, the fixed circle has midpoint (0,0) and radius 2a, the rolling angle of the small circle is 2\varphi and point (2a,0) the starting point (see diagram) then one gets the parametric representation: :x(\varphi) = 3a\cos\varphi- a\cos3\varphi=6a\cos\varphi-4a \cos^3\varphi \ , :y(\varphi) = 3a \sin\varphi - a\sin3\varphi =4a\sin^3\varphi\ , \qquad 0\le \varphi < 2\pi The complex map maps the unit circle to a nephroid [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Evolute
In the differential geometry of curves, the evolute of a curve is the locus of all its centers of curvature. That is to say that when the center of curvature of each point on a curve is drawn, the resultant shape will be the evolute of that curve. The evolute of a circle is therefore a single point at its center. Equivalently, an evolute is the envelope of the normals to a curve. The evolute of a curve, a surface, or more generally a submanifold, is the caustic of the normal map. Let be a smooth, regular submanifold in . For each point in and each vector , based at and normal to , we associate the point . This defines a Lagrangian map, called the normal map. The caustic of the normal map is the evolute of . Evolutes are closely connected to involutes: A curve is the evolute of any of its involutes. History Apollonius ( 200 BC) discussed evolutes in Book V of his ''Conics''. However, Huygens is sometimes credited with being the first to study them (1673). Huygens ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Epicycloid
In geometry, an epicycloid is a plane curve produced by tracing the path of a chosen point on the circumference of a circle—called an ''epicycle''—which rolls without slipping around a fixed circle. It is a particular kind of roulette. Equations If the smaller circle has radius , and the larger circle has radius , then the parametric equations for the curve can be given by either: :\begin & x (\theta) = (R + r) \cos \theta \ - r \cos \left( \frac \theta \right) \\ & y (\theta) = (R + r) \sin \theta \ - r \sin \left( \frac \theta \right) \end or: :\begin & x (\theta) = r (k + 1) \cos \theta - r \cos \left( (k + 1) \theta \right) \\ & y (\theta) = r (k + 1) \sin \theta - r \sin \left( (k + 1) \theta \right) \end in a more concise and complex form :z(\theta) = r \left(e^ - (k + 1)e^ \right) where * angle is in turns: \theta \in , 2\pi * smaller circle has radius * the larger circle has radius Area (Assuming the initial point lies on the larger circle.) When is a pos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Caustic (mathematics)
In differential geometry, a caustic is the envelope of rays either reflected or refracted by a manifold. It is related to the concept of caustics in geometric optics. The ray's source may be a point (called the radiant) or parallel rays from a point at infinity, in which case a direction vector of the rays must be specified. More generally, especially as applied to symplectic geometry and singularity theory, a caustic is the critical value set of a Lagrangian mapping where is a Lagrangian immersion of a Lagrangian submanifold ''L'' into a symplectic manifold ''M'', and is a Lagrangian fibration of the symplectic manifold ''M''. The caustic is a subset of the Lagrangian fibration's base space ''B''. Explanation Concentration of light, especially sunlight, can burn. The word ''caustic'', in fact, comes from the Greek καυστός, burnt, via the Latin ''causticus'', burning. A common situation where caustics are visible is when light shines on a drinking glass. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cardioid
In geometry, a cardioid () is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It can also be defined as an epicycloid having a single cusp. It is also a type of sinusoidal spiral, and an inverse curve of the parabola with the focus as the center of inversion. A cardioid can also be defined as the set of points of reflections of a fixed point on a circle through all tangents to the circle. The name was coined by de Castillon in 1741 but the cardioid had been the subject of study decades beforehand.Yates Named for its heart-like form, it is shaped more like the outline of the cross section of a round apple without the stalk. A cardioid microphone exhibits an acoustic pickup pattern that, when graphed in two dimensions, resembles a cardioid (any 2d plane containing the 3d straight line of the microphone body). In three dimensions, the cardioid is shaped like an apple centred around the microphone which is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radius Of Curvature (mathematics)
In differential geometry, the radius of curvature, , is the reciprocal of the curvature. For a curve, it equals the radius of the circular arc which best approximates the curve at that point. For surfaces, the radius of curvature is the radius of a circle that best fits a normal section or combinations thereof. Definition In the case of a space curve, the radius of curvature is the length of the curvature vector. In the case of a plane curve, then is the absolute value of : R \equiv \left, \frac \ = \frac, where is the arc length from a fixed point on the curve, is the tangential angle and is the curvature. Formula In 2D If the curve is given in Cartesian coordinates as , i.e., as the graph of a function, then the radius of curvature is (assuming the curve is differentiable up to order 2): : R =\left, \frac \, \qquad\mbox\quad y' = \frac,\quad y'' = \frac, and denotes the absolute value of . If the curve is given parametrically by functions and , then the radius ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Caustic00
Caustic most commonly refers to: * Causticity, a property of various corrosive substances ** Sodium hydroxide, sometimes called ''caustic soda'' ** Potassium hydroxide, sometimes called ''caustic potash'' ** Calcium oxide, sometimes called ''caustic lime'' Caustic may also refer to: * Caustic (band), an American industrial/powernoise band * Caustic (mathematics), the envelope of rays reflected or refracted by a manifold * Caustic (optics), optic phenomenon due to light rays reflecting/refracting through curved surfaces/objects * Caustic Graphics, a graphics technology developer, part of Imagination Technologies * Caustic Window, an alias of Aphex Twin (electronic musician Richard D. James) * A playable character in the battle royale game ''Apex Legends ''Apex Legends'' is a free-to-play battle royale-hero shooter game developed by Respawn Entertainment and published by Electronic Arts. It was released for PlayStation 4, Windows, and Xbox One in February 2019, for Ninte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometric Formulae
In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involving certain functions of one or more angles. They are distinct from triangle identities, which are identities potentially involving angles but also involving side lengths or other lengths of a triangle. These identities are useful whenever expressions involving trigonometric functions need to be simplified. An important application is the integration of non-trigonometric functions: a common technique involves first using the substitution rule with a trigonometric function, and then simplifying the resulting integral with a trigonometric identity. Pythagorean identities The basic relationship between the sine and cosine is given by the Pythagorean identity: :\sin^2\theta + \cos^2\theta = 1, where \sin^2 \theta means (\sin \theta)^2 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |