|
Nullcline
In mathematical analysis, nullclines, sometimes called zero-growth isoclines, are encountered in a system of ordinary differential equations :x_1'=f_1(x_1, \ldots, x_n) :x_2'=f_2(x_1, \ldots, x_n) ::\vdots :x_n'=f_n(x_1, \ldots, x_n) where x' here represents a derivative of x with respect to another parameter, such as time t. The j'th nullcline is the geometric shape for which x_j'=0. The equilibrium points of the system are located where all of the nullclines intersect. In a two-dimensional linear system In systems theory, a linear system is a mathematical model of a system based on the use of a linear operator. Linear systems typically exhibit features and properties that are much simpler than the nonlinear case. As a mathematical abstracti ..., the nullclines can be represented by two lines on a two-dimensional plot; in a general two-dimensional system they are arbitrary curves. History The definition, though with the name ’directivity curve’, was used in a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isocline
300px, Fig. 1: Isoclines (blue), slope field (black), and some solution curves (red) of ''y = ''xy''. Given a family of curves, assumed to be differentiable, an isocline for that family is formed by the set of points at which some member of the family attains a given slope. The word comes from the Greek words ἴσος (isos), meaning "same", and the κλίνειν, meaning "make to slope". Generally, an isocline will itself have the shape of a curve or the union of a small number of curves. Isoclines are often used as a graphical method of solving ordinary differential equations. In an equation of the form ''y' = f''(''x'', ''y''), the isoclines are lines in the (''x'', ''y'') plane obtained by setting ''f''(''x'', ''y'') equal to a constant. This gives a series of lines (for different constants) along which the solution curves have the same gradient. By calculating this gradient for each isocline, the slope field can be visualised; making i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Analysis
Analysis is the branch of mathematics dealing with continuous functions, limit (mathematics), limits, and related theories, such as Derivative, differentiation, Integral, integration, measure (mathematics), measure, infinite sequences, series (mathematics), series, and analytic functions. These theories are usually studied in the context of Real number, real and Complex number, complex numbers and Function (mathematics), functions. Analysis evolved from calculus, which involves the elementary concepts and techniques of analysis. Analysis may be distinguished from geometry; however, it can be applied to any Space (mathematics), space of mathematical objects that has a definition of nearness (a topological space) or specific distances between objects (a metric space). History Ancient Mathematical analysis formally developed in the 17th century during the Scientific Revolution, but many of its ideas can be traced back to earlier mathematicians. Early results in analysis were i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordinary Differential Equation
In mathematics, an ordinary differential equation (ODE) is a differential equation whose unknown(s) consists of one (or more) function(s) of one variable and involves the derivatives of those functions. The term ''ordinary'' is used in contrast with the term partial differential equation which may be with respect to ''more than'' one independent variable. Differential equations A linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form :a_0(x)y +a_1(x)y' + a_2(x)y'' +\cdots +a_n(x)y^+b(x)=0, where , ..., and are arbitrary differentiable functions that do not need to be linear, and are the successive derivatives of the unknown function of the variable . Among ordinary differential equations, linear differential equations play a prominent role for several reasons. Most elementary and special functions that are encountered in physics and applied mathem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the "instantaneous rate of change", the ratio of the instantaneous change in the dependent variable to that of the independent variable. Derivatives can be generalized to functions of several real variables. In this generalization, the deriv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
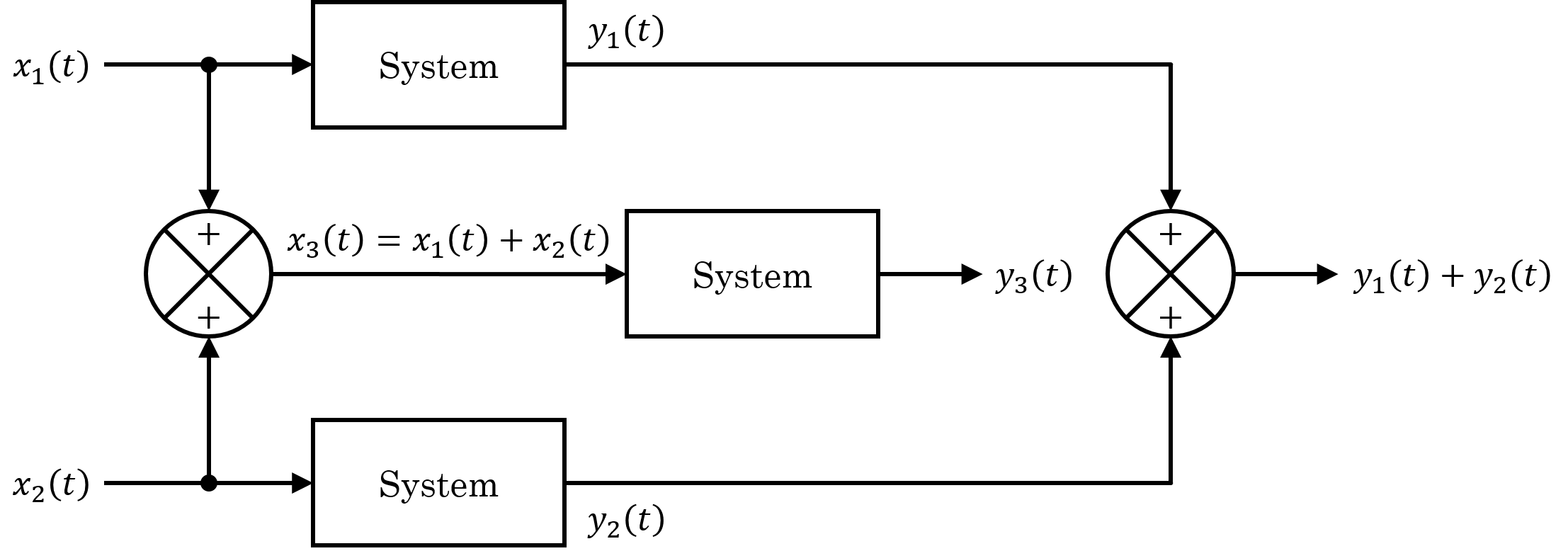
Linear System
In systems theory, a linear system is a mathematical model of a system based on the use of a linear operator. Linear systems typically exhibit features and properties that are much simpler than the nonlinear case. As a mathematical abstraction or idealization, linear systems find important applications in automatic control theory, signal processing, and telecommunications. For example, the propagation medium for wireless communication systems can often be modeled by linear systems. Definition A general deterministic system can be described by an operator, that maps an input, as a function of to an output, a type of black box description. A system is linear if and only if it satisfies the superposition principle, or equivalently both the additivity and homogeneity properties, without restrictions (that is, for all inputs, all scaling constants and all time.) The superposition principle means that a linear combination of inputs to the system produces a linear combin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |