|
Next-generation Matrix
In epidemiology, the next-generation matrix is used to derive the basic reproduction number, for a compartmental model of the spread of infectious diseases. In population dynamics it is used to compute the basic reproduction number for structured population models. It is also used in multi-type branching models for analogous computations. The method to compute the basic reproduction ratio using the next-generation matrix is given by Diekmann ''et al.'' (1990) and van den Driessche and Watmough (2002). To calculate the basic reproduction number by using a next-generation matrix, the whole population is divided into n compartments in which there are m [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Epidemiology
Epidemiology is the study and analysis of the distribution (who, when, and where), patterns and determinants of health and disease conditions in a defined population. It is a cornerstone of public health, and shapes policy decisions and evidence-based practice by identifying risk factors for disease and targets for preventive healthcare. Epidemiologists help with study design, collection, and statistical analysis of data, amend interpretation and dissemination of results (including peer review and occasional systematic review). Epidemiology has helped develop methodology used in clinical research, public health studies, and, to a lesser extent, basic research in the biological sciences. Major areas of epidemiological study include disease causation, transmission, outbreak investigation, disease surveillance, environmental epidemiology, forensic epidemiology, occupational epidemiology, screening, biomonitoring, and comparisons of treatment effects such as in clinical t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Basic Reproduction Number
In epidemiology, the basic reproduction number, or basic reproductive number (sometimes called basic reproduction ratio or basic reproductive rate), denoted R_0 (pronounced ''R nought'' or ''R zero''), of an infection is the expected number of cases directly generated by one case in a population where all individuals are susceptible to infection. The definition assumes that no other individuals are infected or immunized (naturally or through vaccination). Some definitions, such as that of the Australian Department of Health, add the absence of "any deliberate intervention in disease transmission". The basic reproduction number is not necessarily the same as the effective reproduction number R (usually written R_t 't'' for time sometimes R_e), which is the number of cases generated in the current state of a population, which does not have to be the uninfected state. R_0 is a dimensionless number (persons infected per person infecting) and not a time rate, which would have u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compartmental Models In Epidemiology
Compartmental models are a very general modelling technique. They are often applied to the mathematical modelling of infectious diseases. The population is assigned to compartments with labels – for example, S, I, or R, (Susceptible, Infectious, or Recovered). People may progress between compartments. The order of the labels usually shows the flow patterns between the compartments; for example SEIS means susceptible, exposed, infectious, then susceptible again. The origin of such models is the early 20th century, with important works being that of Ross in 1916, Ross and Hudson in 1917, Kermack and McKendrick in 1927 and Kendall in 1956. The Reed-Frost model was also a significant and widely-overlooked ancestor of modern epidemiological modelling approaches. The models are most often run with ordinary differential equations (which are deterministic), but can also be used with a stochastic (random) framework, which is more realistic but much more complicated to analyze. Mod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
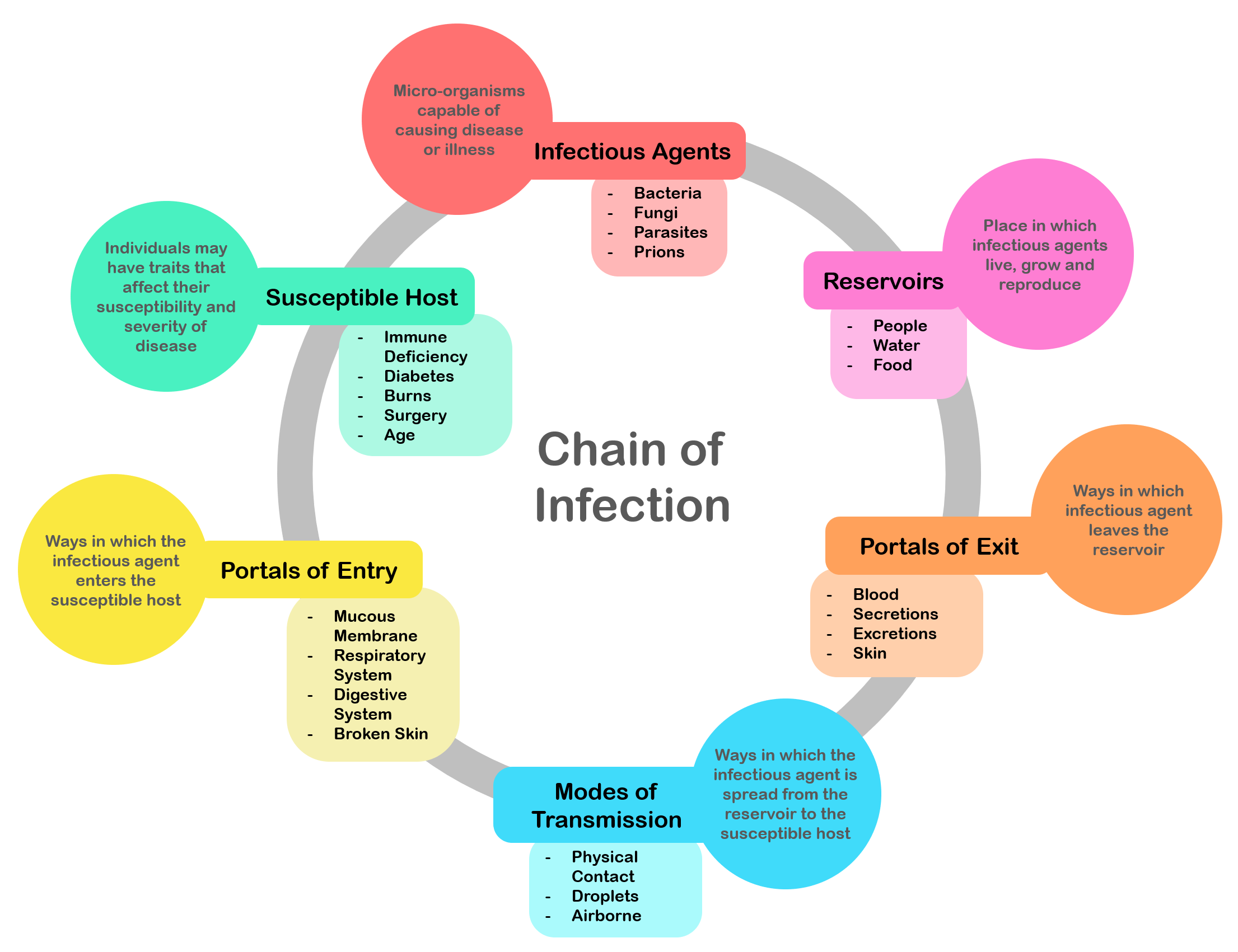
Infectious Disease
An infection is the invasion of tissues by pathogens, their multiplication, and the reaction of host tissues to the infectious agent and the toxins they produce. An infectious disease, also known as a transmissible disease or communicable disease, is an illness resulting from an infection. Infections can be caused by a wide range of pathogens, most prominently bacteria and viruses. Hosts can fight infections using their immune system. Mammalian hosts react to infections with an innate response, often involving inflammation, followed by an adaptive response. Specific medications used to treat infections include antibiotics, antivirals, antifungals, antiprotozoals, and antihelminthics. Infectious diseases resulted in 9.2 million deaths in 2013 (about 17% of all deaths). The branch of medicine that focuses on infections is referred to as infectious disease. Types Infections are caused by infectious agents ( pathogens) including: * Bacteria (e.g. ''Mycobacterium ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Population Dynamics
Population dynamics is the type of mathematics used to model and study the size and age composition of populations as dynamical systems. History Population dynamics has traditionally been the dominant branch of mathematical biology, which has a history of more than 220 years,Malthus, Thomas Robert. An Essay on the Principle of Population: Library of Economics although over the last century the scope of mathematical biology has greatly expanded. The beginning of population dynamics is widely regarded as the work of Malthus, formulated as the Malthusian growth model. According to Malthus, assuming that the conditions (the environment) remain constant ('' ceteris paribus''), a population will grow (or decline) exponentially. This principle provided the basis for the subsequent predictive theories, such as the demographic studies such as the work of Benjamin Gompertz and Pierre François Verhulst in the early 19th century, who refined and adjusted the Malthusian demographic m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Mathematical Biology
'' Journal of Mathematical Biology'' is a peer-reviewed, mathematics journal, published by Springer Verlag. Founded in 1974, the journal publishes articles on mathematical biology. In particular, papers published in this journal 'should either provide biological insight as a result of mathematical analysis or identify and open up challenging new types of mathematical problems that derive from biological knowledge'. It is the official journal of the European Society for Mathematical and Theoretical Biology. The editors-in-chief are Thomas Hillen, Anna Marciniak-Czochra, and Mark Lewis. Its 2020 impact factor is 2.259. Abstracting and indexing This journal is indexed in the following databases: *Thomson Reuters *: BIOSIS *: Biological Abstracts *: Current Contents / Life Sciences *: Journal Citation Reports *: Science Citation Index Expanded *: Zoological Record *: PubMed/Medline ( Web of Knowledge) *Gale *: Academic OneFile *: Expanded Academic *EBSCO host *: Academic Search *: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Epidemic Model
Compartmental models are a very general modelling technique. They are often applied to the mathematical modelling of infectious diseases. The population is assigned to compartments with labels – for example, S, I, or R, (Susceptible, Infectious, or Recovered). People may progress between compartments. The order of the labels usually shows the flow patterns between the compartments; for example SEIS means susceptible, exposed, infectious, then susceptible again. The origin of such models is the early 20th century, with important works being that of Ross in 1916, Ross and Hudson in 1917, Kermack and McKendrick in 1927 and Kendall in 1956. The Reed-Frost model was also a significant and widely-overlooked ancestor of modern epidemiological modelling approaches. The models are most often run with ordinary differential equations (which are deterministic), but can also be used with a stochastic (random) framework, which is more realistic but much more complicated to analyze. Models ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jacobian Matrix
In vector calculus, the Jacobian matrix (, ) of a vector-valued function of several variables is the matrix of all its first-order partial derivatives. When this matrix is square, that is, when the function takes the same number of variables as input as the number of vector components of its output, its determinant is referred to as the Jacobian determinant. Both the matrix and (if applicable) the determinant are often referred to simply as the Jacobian in literature. Suppose is a function such that each of its first-order partial derivatives exist on . This function takes a point as input and produces the vector as output. Then the Jacobian matrix of is defined to be an matrix, denoted by , whose th entry is \mathbf J_ = \frac, or explicitly :\mathbf J = \begin \dfrac & \cdots & \dfrac \end = \begin \nabla^ f_1 \\ \vdots \\ \nabla^ f_m \end = \begin \dfrac & \cdots & \dfrac\\ \vdots & \ddots & \vdots\\ \dfrac & \cdo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalues And Eigenvectors
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by \lambda, is the factor by which the eigenvector is scaled. Geometrically, an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction in which it is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed. Loosely speaking, in a multidimensional vector space, the eigenvector is not rotated. Formal definition If is a linear transformation from a vector space over a field into itself and is a nonzero vector in , then is an eigenvector of if is a scalar multiple of . This can be written as T(\mathbf) = \lambda \mathbf, where is a scalar in , known as the eigenvalue, characteristic value, or characteristic root ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Radius
In mathematics, the spectral radius of a square matrix is the maximum of the absolute values of its eigenvalues. More generally, the spectral radius of a bounded linear operator is the supremum of the absolute values of the elements of its spectrum. The spectral radius is often denoted by . Definition Matrices Let be the eigenvalues of a matrix . The spectral radius of is defined as :\rho(A) = \max \left \. The spectral radius can be thought of as an infimum of all norms of a matrix. Indeed, on the one hand, \rho(A) \leqslant \, A\, for every natural matrix norm \, \cdot\, ; and on the other hand, Gelfand's formula states that \rho(A) = \lim_ \, A^k\, ^ . Both of these results are shown below. However, the spectral radius does not necessarily satisfy \, A\mathbf\, \leqslant \rho(A) \, \mathbf\, for arbitrary vectors \mathbf \in \mathbb^n . To see why, let r > 1 be arbitrary and consider the matrix : C_r = \begin 0 & r^ \\ r & 0 \end . The characteristic polynomia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Modelling Of Infectious Disease
Mathematical models can project how infectious diseases progress to show the likely outcome of an epidemic (including in plants) and help inform public health and plant health interventions. Models use basic assumptions or collected statistics along with mathematics to find parameters for various infectious diseases and use those parameters to calculate the effects of different interventions, like mass vaccination programs. The modelling can help decide which intervention(s) to avoid and which to trial, or can predict future growth patterns, etc. History The modeling of infectious diseases is a tool that has been used to study the mechanisms by which diseases spread, to predict the future course of an outbreak and to evaluate strategies to control an epidemic. The first scientist who systematically tried to quantify causes of death was John Graunt in his book ''Natural and Political Observations made upon the Bills of Mortality'', in 1662. The bills he studied were listings of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrices
Matrix most commonly refers to: * ''The Matrix'' (franchise), an American media franchise ** ''The Matrix'', a 1999 science-fiction action film ** "The Matrix", a fictional setting, a virtual reality environment, within ''The Matrix'' (franchise) * Matrix (mathematics), a rectangular array of numbers, symbols or expressions Matrix (or its plural form matrices) may also refer to: Science and mathematics * Matrix (mathematics), algebraic structure, extension of vector into 2 dimensions * Matrix (logic), part of a formula in prenex normal form * Matrix (biology), the material in between a eukaryotic organism's cells * Matrix (chemical analysis), the non-analyte components of a sample * Matrix (geology), the fine-grained material in which larger objects are embedded * Matrix (composite), the constituent of a composite material * Hair matrix, produces hair * Nail matrix, part of the nail in anatomy Arts and entertainment Fictional entities * Matrix (comics), two comic b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |