|
Multimodal Logic
A multimodal logic is a modal logic that has more than one primitive modal operator. They find substantial applications in theoretical computer science. Overview A modal logic with ''n'' primitive unary modal operators \Box_i, i\in \ is called an ''n''-modal logic. Given these operators and negation, one can always add \Diamond_i modal operators defined as \Diamond_i P if and only if \lnot \Box_i \lnot P, to give a classical multimodal logic if it is in addition stable under necessitation (or "possibilization", therefore) of both members of provable equivalences. Perhaps the first substantive example of a two-modal logic is Arthur Prior's tense logic, with two modalities, F and P, corresponding to "sometime in the future" and "sometime in the past". A logic with infinitely many modalities is dynamic logic, introduced by Vaughan Pratt in 1976 and having a separate modal operator for every regular expression. A version of temporal logic introduced in 1977 and intended for program v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Modal Logic
Modal logic is a kind of logic used to represent statements about Modality (natural language), necessity and possibility. In philosophy and related fields it is used as a tool for understanding concepts such as knowledge, obligation, and causality, causation. For instance, in epistemic modal logic, the well-formed_formula, formula \Box P can be used to represent the statement that P is known. In deontic modal logic, that same formula can represent that P is a moral obligation. Modal logic considers the inferences that modal statements give rise to. For instance, most epistemic modal logics treat the formula \Box P \rightarrow P as a Tautology_(logic), tautology, representing the principle that only true statements can count as knowledge. However, this formula is not a tautology in deontic modal logic, since what ought to be true can be false. Modal logics are formal systems that include unary operation, unary operators such as \Diamond and \Box, representing possibility and necessi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Modal μ-calculus
In theoretical computer science, the modal μ-calculus (Lμ, Lμ, sometimes just μ-calculus, although this can have a more general meaning) is an extension of propositional modal logic (with many modalities) by adding the least fixed point operator μ and the greatest fixed point operator ν, thus a fixed-point logic. The (propositional, modal) μ-calculus originates with Dana Scott and Jaco de Bakker, and was further developed by Dexter Kozen into the version most used nowadays. It is used to describe properties of labelled transition systems and for verifying these properties. Many temporal logics can be encoded in the μ-calculus, including CTL* and its widely used fragments—linear temporal logic and computational tree logic. An algebraic view is to see it as an algebra of monotonic functions over a complete lattice, with operators consisting of functional composition plus the least and greatest fixed point operators; from this viewpoint, the modal μ-calculus is o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Dov M
DOV or Dov could refer to: ''דב'' or ''דוב'', a Hebrew male given name meaning "bear", from which the Yiddish name " Ber" (בער) was derived (cognate with "bear") which was common among East European Jews. People * Dov J. Elkabas (1968), Amsterdam (Dutch) born musician and producer * Dov Ber of Mezeritch (1700/1704/1710?–1772 OS), second leader and main architect of Hasidic Judaism * Dov Ber Abramowitz (1860–1926), American Orthodox rabbi and author * Dov Charney (born 1969), president and chief executive officer of clothing manufacturer American Apparel * Dov Feigin (1907–2000), Israeli sculptor * Dov Forman (born 2003), English born Author and social media star * Dov Frohman (born 1939), Israeli electrical engineer and business executive * Dov Gabbay (born 1945), logician and professor of logic and computer science * Dov Groverman (born 1965), Israeli Olympic wrestler * Dov Grumet-Morris (born 1982), American ice hockey player * Dov Gruner (1912–1947), Jewish ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
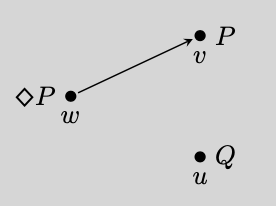
Accessibility Relation
An accessibility relation is a relation (math), relation which plays a key role in assigning truth values to sentences in the Kripke semantics, relational semantics for modal logic. In relational semantics, a modal formula's truth value at a ''possible world'' w can depend on what is true at another possible world v, but only if the accessibility relation R relates w to v. For instance, if P holds at some world v such that wRv, the formula \Diamond P will be true at w. The fact wRv is crucial. If R did not relate w to v, then \Diamond P would be false at w unless P also held at some other world u such that wRu. Accessibility relations are motivated conceptually by the fact that natural language linguistic modality, modal statements depend on some, but not all, alternative scenarios. For instance, the sentence "It might be raining" is not generally judged true simply because one can imagine a scenario where it is raining. Rather, its truth depends on whether such a scenario is r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Kripke Semantics
Kripke semantics (also known as relational semantics or frame semantics, and often confused with possible world semantics) is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke and André Joyal. It was first conceived for modal logics, and later adapted to intuitionistic logic and other non-classical systems. The development of Kripke semantics was a breakthrough in the theory of non-classical logics, because the model theory of such logics was almost non-existent before Kripke (algebraic semantics existed, but were considered 'syntax in disguise'). Semantics of modal logic The language of propositional modal logic consists of a countably infinite set of propositional variables, a set of truth-functional connectives (in this article \to and \neg), and the modal operator \Box ("necessarily"). The modal operator \Diamond ("possibly") is (classically) the dual of \Box and may be defined in terms of necessity like so: \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Possible World Semantics
A possible world is a complete and consistent way the world is or could have been. Possible worlds are widely used as a formal device in logic, philosophy, and linguistics in order to provide a semantics for intensional and modal logic. Their metaphysical status has been a subject of controversy in philosophy, with modal realists such as David Lewis arguing that they are literally existing alternate realities, and others such as Robert Stalnaker arguing that they are not. Logic Possible worlds are one of the foundational concepts in modal and intensional logics. Formulas in these logics are used to represent statements about what ''might'' be true, what ''should'' be true, what one ''believes'' to be true and so forth. To give these statements a formal interpretation, logicians use structures containing possible worlds. For instance, in the relational semantics for classical propositional modal logic, the formula \Diamond P (read as "possibly P") is actually true if and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Epistemic
Epistemology is the branch of philosophy that examines the nature, origin, and limits of knowledge. Also called "the theory of knowledge", it explores different types of knowledge, such as propositional knowledge about facts, practical knowledge in the form of skills, and knowledge by acquaintance as a familiarity through experience. Epistemologists study the concepts of belief, truth, and justification to understand the nature of knowledge. To discover how knowledge arises, they investigate sources of justification, such as perception, introspection, memory, reason, and testimony. The school of skepticism questions the human ability to attain knowledge while fallibilism says that knowledge is never certain. Empiricists hold that all knowledge comes from sense experience, whereas rationalists believe that some knowledge does not depend on it. Coherentists argue that a belief is justified if it coheres with other beliefs. Foundationalists, by contrast, maintain that the justi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Subject (philosophy)
The distinction between subject and object is a basic idea of philosophy. *A subject is a being that exercises agency, undergoes conscious experiences, and is situated in relation to other things that exist outside itself; thus, a subject is any individual, person, or observer. *An object is any of the things observed or experienced by a subject, which may even include other beings (thus, from their own points of view: other subjects). A simple common differentiation for ''subject'' and ''object'' is: an observer versus a thing that is observed. In certain cases involving personhood, subjects and objects can be considered interchangeable where each label is applied only from one or the other point of view. Subjects and objects are related to the philosophical distinction between subjectivity and objectivity: the existence of knowledge, ideas, or information either dependent upon a subject (subjectivity) or independent from any subject (objectivity). Etymology In English the word ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Epistemic Logic
Epistemic modal logic is a subfield of modal logic that is concerned with reasoning about knowledge. While epistemology has a long philosophical tradition dating back to Ancient Greece, epistemic logic is a much more recent development with applications in many fields, including philosophy, theoretical computer science, artificial intelligence, economics, and linguistics. While philosophers since Aristotle have discussed modal logic, and Medieval philosophers such as Avicenna, Ockham, and Duns Scotus developed many of their observations, it was C. I. Lewis who created the first symbolic and systematic approach to the topic, in 1912. It continued to mature as a field, reaching its modern form in 1963 with the work of Saul Kripke. Historical development Many papers were written in the 1950s that spoke of a logic of knowledge in passing, but the Finnish philosopher G. H. von Wright's 1951 paper titled ''An Essay in Modal Logic'' is seen as a founding document. It was not unti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Knowledge Representation
Knowledge representation (KR) aims to model information in a structured manner to formally represent it as knowledge in knowledge-based systems whereas knowledge representation and reasoning (KRR, KR&R, or KR²) also aims to understand, reason, and interpret knowledge. KRR is widely used in the field of artificial intelligence (AI) with the goal to represent information about the world in a form that a computer system can use to solve complex tasks, such as diagnosing a medical condition or having a natural-language dialog. KR incorporates findings from psychology about how humans solve problems and represent knowledge, in order to design formalisms that make complex systems easier to design and build. KRR also incorporates findings from logic to automate various kinds of ''reasoning''. Traditional KRR focuses more on the declarative representation of knowledge. Related knowledge representation formalisms mainly include vocabularies, thesaurus, semantic networks, axiom system ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Fixed-point Logic
In mathematical logic, fixed-point logics are extensions of classical predicate logic that have been introduced to express recursion. Their development has been motivated by descriptive complexity theory and their relationship to database query languages, in particular to Datalog. Least fixed-point logic was first studied systematically by Yiannis N. Moschovakis in 1974, and it was introduced to computer scientists in 1979, when Alfred Aho and Jeffrey Ullman suggested fixed-point logic as an expressive database query language. Partial fixed-point logic For a relational signature ''X'', FO FP''X'') is the set of formulas formed from ''X'' using first-order connectives and predicates, second-order variables as well as a partial fixed point operator \operatorname used to form formulas of the form operatorname_ \varphivec, where P is a second-order variable, \vec a tuple of first-order variables, \vec a tuple of terms and the lengths of \vec and \vec coincide with the arity of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |