|
Molecular Orbitals
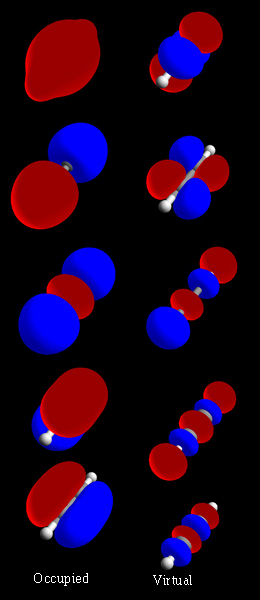
In chemistry, a molecular orbital is a mathematical function describing the location and wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The terms ''atomic orbital'' and ''molecular orbital'' were introduced by Robert S. Mulliken in 1932 to mean ''one-electron orbital wave functions''. At an elementary level, they are used to describe the ''region'' of space in which a function has a significant amplitude. In an isolated atom, the orbital electrons' location is determined by functions called atomic orbitals. When multiple atoms combine chemically into a molecule, the electrons' locations are determined by the molecule as a whole, so the atomic orbitals combine to form molecular orbitals. The electrons from the constituent atoms occupy the molecular orbitals. Mathematically, molecular orbitals are an approximate solution to the Schrödin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbitals Acetylene
Orbital may refer to: Sciences Chemistry and physics * Atomic orbital * Molecular orbital * Hybrid orbital Astronomy and space flight * Orbit ** Earth orbit Medicine and physiology * Orbit (anatomy), also known as the ''orbital bone'' * Orbitofrontal cortex, a part of the brain used for decision making Business * Orbital Corporation, an Australian engine technology company * Orbital Sciences Corporation, a U.S. satellite launch and defense systems corporation * Orbital ATK, American aerospace manufacturer formed from the merger of Orbital Sciences Corporation and parts of Alliant Techsystems Transportation * Ring road (or ''orbital road'' in some regions) * Orbital (metro), a rapid transit line usually encircling a city centre * Orbital engine Other uses * Orbital (The Culture), artificial worlds from Iain M. Banks's series of science fiction novels, the Culture * Orbital (band), an English electronic dance music duo ** ''Orbital'' (1991 album) ** ''Orbital'' (1993 album ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hartree–Fock Method
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state. The Hartree–Fock method often assumes that the exact ''N''-body wave function of the system can be approximated by a single Slater determinant (in the case where the particles are fermions) or by a single permanent (in the case of bosons) of ''N'' spin-orbitals. By invoking the variational method, one can derive a set of ''N''-coupled equations for the ''N'' spin orbitals. A solution of these equations yields the Hartree–Fock wave function and energy of the system. Especially in the older literature, the Hartree–Fock method is also called the self-consistent field method (SCF). In deriving what is now called the Hartree equation as an approximate solution of the Schrödinger equation, Hartree required the final field as computed from the charge distribution to be "s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
