|
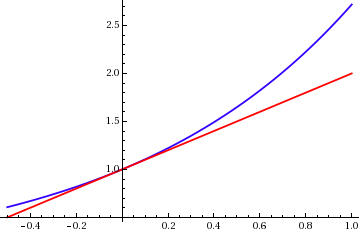
Methods Of Computing Square Roots
Methods of computing square roots are numerical analysis algorithms for approximating the principal, or non-negative, square root (usually denoted \sqrt, \sqrt /math>, or S^) of a real number. Arithmetically, it means given S, a procedure for finding a number which when multiplied by itself, yields S; algebraically, it means a procedure for finding the non-negative root of the equation x^2-S=0; geometrically, it means given two line segments, a procedure for constructing their geometric mean. Every real number except zero has two square roots. In addition to the principal square root, there is a negative square root equal in magnitude but opposite in sign to the principal square root, except for zero, which has double square roots of zero. The principal square root of most numbers is an irrational number with an infinite decimal expansion. As a result, the decimal expansion of any such square root can only be computed to some finite-precision approximation. However, even if we ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer Square Root
In number theory, the integer square root (isqrt) of a non-negative integer ''n'' is the non-negative integer ''m'' which is the greatest integer less than or equal to the square root of ''n'', : \mbox( n ) = \lfloor \sqrt n \rfloor. For example, \mbox(27) = \lfloor \sqrt \rfloor = \lfloor 5.19615242270663 ... \rfloor = 5. Introductory remark Let y \text k be non-negative integers. Algorithms that compute (the decimal representation of) \sqrt y run forever on each input y which is not a perfect square. Algorithms that compute \lfloor \sqrt y \rfloor do not run forever. They are nevertheless capable of computing \sqrt y up to any desired accuracy k. Choose any k and compute \lfloor \sqrt \rfloor. For example (setting y = 2): :\begin & k = 0: \lfloor \sqrt \rfloor = \lfloor \sqrt \rfloor = 1 \\ & k = 1: \lfloor \sqrt \rfloor = \lfloor \sqrt \rfloor = 14 \\ & k = 2: \lfloor \sqrt \rfloor = \lfloor \sqrt \rfloor = 141 \\ & k = 3: \lfloor \sqrt \rfloor = \lfloor \sqrt \r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods that attempt at finding approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics (predicting the motions of planets, stars and galaxies), numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living cells in medicine an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Root
In mathematics, a square root of a number is a number such that ; in other words, a number whose ''square'' (the result of multiplying the number by itself, or ⋅ ) is . For example, 4 and −4 are square roots of 16, because . Every nonnegative real number has a unique nonnegative square root, called the ''principal square root'', which is denoted by \sqrt, where the symbol \sqrt is called the '' radical sign'' or ''radix''. For example, to express the fact that the principal square root of 9 is 3, we write \sqrt = 3. The term (or number) whose square root is being considered is known as the ''radicand''. The radicand is the number or expression underneath the radical sign, in this case 9. For nonnegative , the principal square root can also be written in exponent notation, as . Every positive number has two square roots: \sqrt, which is positive, and -\sqrt, which is negative. The two roots can be written more concisely using the ± sign as \plusmn\sq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Napier's Bones
Napier's bones is a manually-operated calculating device created by John Napier of Merchiston, Scotland for the calculation of products and quotients of numbers. The method was based on lattice multiplication, and also called ''rabdology'', a word invented by Napier. Napier published his version in 1617. It was printed in Edinburgh and dedicated to his patron Alexander Seton. Using the multiplication tables embedded in the rods, multiplication can be reduced to addition operations and division to subtractions. Advanced use of the rods can extract square roots. Napier's bones are not the same as logarithms, with which Napier's name is also associated, but are based on dissected multiplication tables. The complete device usually includes a base board with a rim; the user places Napier's rods inside the rim to conduct multiplication or division. The board's left edge is divided into nine squares, holding the numbers 1 to 9. In Napier's original design, the rods are made of metal, wo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numeral System
A numeral system (or system of numeration) is a writing system for expressing numbers; that is, a mathematical notation for representing numbers of a given set, using digits or other symbols in a consistent manner. The same sequence of symbols may represent different numbers in different numeral systems. For example, "11" represents the number ''eleven'' in the decimal numeral system (used in common life), the number ''three'' in the binary numeral system (used in computers), and the number ''two'' in the unary numeral system (e.g. used in tallying scores). The number the numeral represents is called its value. Not all number systems can represent all numbers that are considered in the modern days; for example, Roman numerals have no zero. Ideally, a numeral system will: *Represent a useful set of numbers (e.g. all integers, or rational numbers) *Give every number represented a unique representation (or at least a standard representation) *Reflect the algebraic and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Number
In mathematics, a square number or perfect square is an integer that is the square of an integer; in other words, it is the product of some integer with itself. For example, 9 is a square number, since it equals and can be written as . The usual notation for the square of a number is not the product , but the equivalent exponentiation , usually pronounced as " squared". The name ''square'' number comes from the name of the shape. The unit of area is defined as the area of a unit square (). Hence, a square with side length has area . If a square number is represented by ''n'' points, the points can be arranged in rows as a square each side of which has the same number of points as the square root of ''n''; thus, square numbers are a type of figurate numbers (other examples being cube numbers and triangular numbers). Square numbers are non-negative. A non-negative integer is a square number when its square root is again an integer. For example, \sqrt = 3, so 9 is a squ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Theorem
In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the polynomial into a sum involving terms of the form , where the exponents and are nonnegative integers with , and the coefficient of each term is a specific positive integer depending on and . For example, for , (x+y)^4 = x^4 + 4 x^3y + 6 x^2 y^2 + 4 x y^3 + y^4. The coefficient in the term of is known as the binomial coefficient \tbinom or \tbinom (the two have the same value). These coefficients for varying and can be arranged to form Pascal's triangle. These numbers also occur in combinatorics, where \tbinom gives the number of different combinations of elements that can be chosen from an -element set. Therefore \tbinom is often pronounced as " choose ". History Special cases of the binomial theorem were known since at least the 4th century BC when Greek mathematician Euclid mentione ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Methods Of Computing Square Roots
Methods of computing square roots are numerical analysis algorithms for approximating the principal, or non-negative, square root (usually denoted \sqrt, \sqrt /math>, or S^) of a real number. Arithmetically, it means given S, a procedure for finding a number which when multiplied by itself, yields S; algebraically, it means a procedure for finding the non-negative root of the equation x^2-S=0; geometrically, it means given two line segments, a procedure for constructing their geometric mean. Every real number except zero has two square roots. In addition to the principal square root, there is a negative square root equal in magnitude but opposite in sign to the principal square root, except for zero, which has double square roots of zero. The principal square root of most numbers is an irrational number with an infinite decimal expansion. As a result, the decimal expansion of any such square root can only be computed to some finite-precision approximation. However, even if we ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pakistan
Pakistan ( ur, ), officially the Islamic Republic of Pakistan ( ur, , label=none), is a country in South Asia. It is the world's List of countries and dependencies by population, fifth-most populous country, with a population of almost 243 million people, and has the world's Islam by country#Countries, second-largest Muslim population just behind Indonesia. Pakistan is the List of countries and dependencies by area, 33rd-largest country in the world by area and 2nd largest in South Asia, spanning . It has a coastline along the Arabian Sea and Gulf of Oman in the south, and is bordered by India to India–Pakistan border, the east, Afghanistan to Durand Line, the west, Iran to Iran–Pakistan border, the southwest, and China to China–Pakistan border, the northeast. It is separated narrowly from Tajikistan by Afghanistan's Wakhan Corridor in the north, and also shares a maritime border with Oman. Islamabad is the nation's capital, while Karachi is its largest city and fina ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
South Asian
South Asia is the southern Subregion#Asia, subregion of Asia, which is defined in both geography, geographical and culture, ethno-cultural terms. The region consists of the countries of Afghanistan, Bangladesh, Bhutan, India, Maldives, Nepal, Pakistan, and Sri Lanka.;;;;;;;; Topographically, it is dominated by the Indian subcontinent and defined largely by the Indian Ocean on the south, and the Himalayas, Karakoram, and Pamir Mountains, Pamir mountains on the north. The Amu Darya, which rises north of the Hindu Kush, forms part of the northwestern border. On land (clockwise), South Asia is bounded by Western Asia, Central Asia, East Asia, and Southeast Asia. The South Asian Association for Regional Cooperation (SAARC) is an economic cooperation organization in the region which was established in 1985 and includes all eight nations comprising South Asia. South Asia covers about , which is 11.71% of the Asian continent or 3.5% of the world's land surface area. The population of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Relative Error
The approximation error in a data value is the discrepancy between an exact value and some ''approximation'' to it. This error can be expressed as an absolute error (the numerical amount of the discrepancy) or as a relative error (the absolute error divided by the data value). An approximation error can occur because of computing machine precision or measurement error (e.g. the length of a piece of paper is 4.53 cm but the ruler only allows you to estimate it to the nearest 0.1 cm, so you measure it as 4.5 cm). In the mathematical field of numerical analysis, the numerical stability of an algorithm indicates how the error is propagated by the algorithm. Formal definition One commonly distinguishes between the relative error and the absolute error. Given some value ''v'' and its approximation ''v''approx, the absolute error is :\epsilon = , v-v_\text, \ , where the vertical bars denote the absolute value. If v \ne 0, the relative error is : \eta = \frac = \left, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |