|
Maximum Entropy Principle
The principle of maximum entropy states that the probability distribution which best represents the current state of knowledge about a system is the one with largest entropy, in the context of precisely stated prior data (such as a proposition that expresses testable information). Another way of stating this: Take precisely stated prior data or testable information about a probability distribution function. Consider the set of all trial probability distributions that would encode the prior data. According to this principle, the distribution with maximal information entropy is the best choice. History The principle was first expounded by E. T. Jaynes in two papers in 1957 where he emphasized a natural correspondence between statistical mechanics and information theory. In particular, Jaynes offered a new and very general rationale why the Gibbsian method of statistical mechanics works. He argued that the entropy of statistical mechanics and the information entropy of informatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that the coin is fair). Examples of random phenomena include the weather conditions at some future date, the height of a randomly selected person, the fraction of male students in a school, the results of a survey to be conducted, etc. Introduction A probability distribution is a mathematical description of the probabilities of events, subsets of the sample space. The sample space, often denoted by \Omega, is the set of all possible outcomes of a random phe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ergodic
In mathematics, ergodicity expresses the idea that a point of a moving system, either a dynamical system or a stochastic process, will eventually visit all parts of the space that the system moves in, in a uniform and random sense. This implies that the average behavior of the system can be deduced from the trajectory of a "typical" point. Equivalently, a sufficiently large collection of random samples from a process can represent the average statistical properties of the entire process. Ergodicity is a property of the system; it is a statement that the system cannot be reduced or factored into smaller components. Ergodic theory is the study of systems possessing ergodicity. Ergodic systems occur in a broad range of systems in physics and in geometry. This can be roughly understood to be due to a common phenomenon: the motion of particles, that is, geodesics on a hyperbolic manifold are divergent; when that manifold is compact, that is, of finite size, those orbits return to the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logistic Regression
In statistics, the logistic model (or logit model) is a statistical model that models the probability of an event taking place by having the log-odds for the event be a linear function (calculus), linear combination of one or more independent variables. In regression analysis, logistic regression (or logit regression) is estimation theory, estimating the parameters of a logistic model (the coefficients in the linear combination). Formally, in binary logistic regression there is a single binary variable, binary dependent variable, coded by an indicator variable, where the two values are labeled "0" and "1", while the independent variables can each be a binary variable (two classes, coded by an indicator variable) or a continuous variable (any real value). The corresponding probability of the value labeled "1" can vary between 0 (certainly the value "0") and 1 (certainly the value "1"), hence the labeling; the function that converts log-odds to probability is the logistic function, h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Language Processing
Natural language processing (NLP) is an interdisciplinary subfield of linguistics, computer science, and artificial intelligence concerned with the interactions between computers and human language, in particular how to program computers to process and analyze large amounts of natural language data. The goal is a computer capable of "understanding" the contents of documents, including the contextual nuances of the language within them. The technology can then accurately extract information and insights contained in the documents as well as categorize and organize the documents themselves. Challenges in natural language processing frequently involve speech recognition, natural-language understanding, and natural-language generation. History Natural language processing has its roots in the 1950s. Already in 1950, Alan Turing published an article titled "Computing Machinery and Intelligence" which proposed what is now called the Turing test as a criterion of intelligence, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Kinematics
Radical probabilism is a hypothesis in philosophy, in particular epistemology, and probability theory that holds that no facts are known for certain. That view holds profound implications for statistical inference. The philosophy is particularly associated with Richard Jeffrey who wittily characterised it with the ''dictum'' "It's probabilities all the way down." Background Bayes' theorem states a rule for updating a probability conditioned on other information. In 1967, Ian Hacking argued that in a static form, Bayes' theorem only connects probabilities that are held simultaneously; it does not tell the learner how to update probabilities when new evidence becomes available over time, contrary to what contemporary Bayesians suggested. According to Hacking, adopting Bayes' theorem is a temptation. Suppose that a learner forms probabilities ''P''old(''A'' & ''B'') = ''p'' and ''P''old(''B'') = ''q''. If the learner subsequently learns that ''B'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Richard Jeffrey
Richard Carl Jeffrey (August 5, 1926 – November 9, 2002) was an American philosopher, logician, and probability theorist. He is best known for developing and championing the philosophy of radical probabilism and the associated heuristic of probability kinematics, also known as Jeffrey conditioning. Life and career Born in Boston, Massachusetts, Jeffrey served in the U.S. Navy during World War II. As a graduate student he studied under Rudolf Carnap and Carl Hempel. He received his M.A. from the University of Chicago in 1952 and his Ph.D. from Princeton in 1957. After holding academic positions at MIT, City College of New York, Stanford University, and the University of Pennsylvania, he joined the faculty of Princeton in 1974 and became a professor emeritus there in 1999. He was also a visiting professor at the University of California, Irvine. Jeffrey, who died of lung cancer at the age of 76, was known for his sense of humor, which often came through in his breezy writin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radical Probabilism
Radical probabilism is a hypothesis in philosophy, in particular epistemology, and probability theory that holds that no facts are known for certain. That view holds profound implications for statistical inference. The philosophy is particularly associated with Richard Jeffrey who wittily characterised it with the ''dictum'' "It's probabilities all the way down." Background Bayes' theorem states a rule for updating a probability conditioned on other information. In 1967, Ian Hacking argued that in a static form, Bayes' theorem only connects probabilities that are held simultaneously; it does not tell the learner how to update probabilities when new evidence becomes available over time, contrary to what contemporary Bayesians suggested. According to Hacking, adopting Bayes' theorem is a temptation. Suppose that a learner forms probabilities ''P''old(''A'' & ''B'') = ''p'' and ''P''old(''B'') = ''q''. If the learner subsequently learns that ''B'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of The American Statistical Association
The ''Journal of the American Statistical Association (JASA)'' is the primary journal published by the American Statistical Association, the main professional body for statisticians in the United States. It is published four times a year in March, June, September and December by Taylor & Francis, Ltd on behalf of the American Statistical Association. As a statistics journal it publishes articles primarily focused on the application of statistics, statistical theory and methods in economic, social, physical, engineering, and health sciences. The journal also includes reviews of academic books which are important to the advancement of the field. It had an impact factor of 2.063 in 2010, tenth highest in the "Statistics and Probability" category of ''Journal Citation Reports''. In a 2003 survey of statisticians, the ''Journal of the American Statistical Association'' was ranked first, among all journals, for "Applications of Statistics" and second (after ''Annals of Statistics'') f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Econometrics
The ''Journal of Econometrics'' is a scholarly journal in econometrics. It was first published in 1973. Its current managing editors are Serena Ng and Elie Tamer, Torben Andersen and Xiaohong Chen serve as editors. The journal publishes work dealing with estimation and other methodological aspects of the application of statistical inference to economic data, as well as papers dealing with the application of econometric techniques to economics. The journal also publishes a supplement to the Journal of Econometrics which is called "Annals of Econometrics". Each issue of the Annals includes a collection of papers on a single topic selected by the editor of the issue. See also * ''Econometrics Journal'' References External links Homepage Econometrics, Journal of Econometrics journals Econometrics Econometrics is the application of Statistics, statistical methods to economic data in order to give Empirical evidence, empirical content to economic relationships.M. Hashem P ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
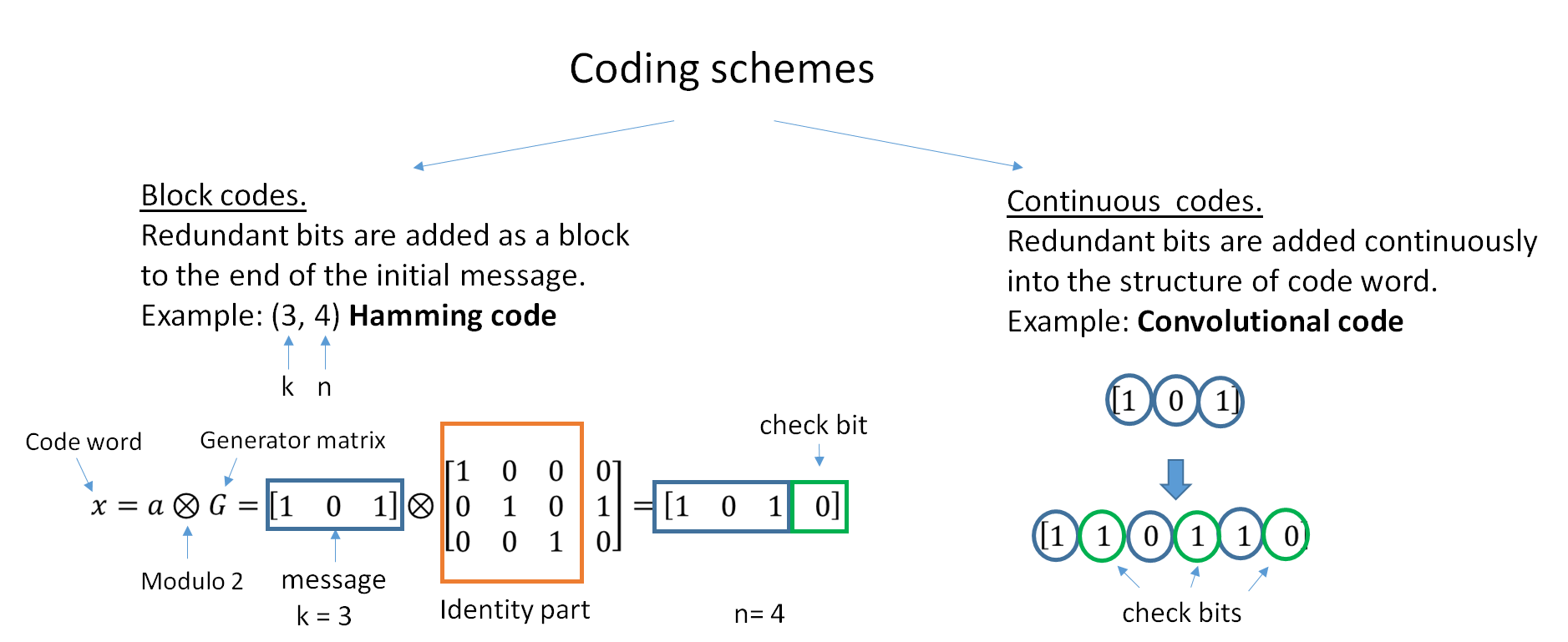
Channel Coding
In computing, telecommunication, information theory, and coding theory, an error correction code, sometimes error correcting code, (ECC) is used for controlling errors in data over unreliable or noisy communication channels. The central idea is the sender encodes the message with redundant information in the form of an ECC. The redundancy allows the receiver to detect a limited number of errors that may occur anywhere in the message, and often to correct these errors without retransmission. The American mathematician Richard Hamming pioneered this field in the 1940s and invented the first error-correcting code in 1950: the Hamming (7,4) code. ECC contrasts with error detection in that errors that are encountered can be corrected, not simply detected. The advantage is that a system using ECC does not require a reverse channel to request retransmission of data when an error occurs. The downside is that there is a fixed overhead that is added to the message, thereby requiring a h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Inference
Bayesian inference is a method of statistical inference in which Bayes' theorem is used to update the probability for a hypothesis as more evidence or information becomes available. Bayesian inference is an important technique in statistics, and especially in mathematical statistics. Bayesian updating is particularly important in the dynamic analysis of a sequence of data. Bayesian inference has found application in a wide range of activities, including science, engineering, philosophy, medicine, sport, and law. In the philosophy of decision theory, Bayesian inference is closely related to subjective probability, often called "Bayesian probability". Introduction to Bayes' rule Formal explanation Bayesian inference derives the posterior probability as a consequence of two antecedents: a prior probability and a "likelihood function" derived from a statistical model for the observed data. Bayesian inference computes the posterior probability according to Bayes' theorem: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Distribution (discrete)
In probability theory and statistics, the discrete uniform distribution is a symmetric probability distribution wherein a finite number of values are equally likely to be observed; every one of ''n'' values has equal probability 1/''n''. Another way of saying "discrete uniform distribution" would be "a known, finite number of outcomes equally likely to happen". A simple example of the discrete uniform distribution is throwing a fair dice. The possible values are 1, 2, 3, 4, 5, 6, and each time the die is thrown the probability of a given score is 1/6. If two dice are thrown and their values added, the resulting distribution is no longer uniform because not all sums have equal probability. Although it is convenient to describe discrete uniform distributions over integers, such as this, one can also consider discrete uniform distributions over any finite set. For instance, a random permutation is a permutation generated uniformly from the permutations of a given length, and a unif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |