|
Monogamy Of Entanglement
In quantum physics, the "monogamy" of quantum entanglement refers to the fundamental property that it cannot be freely shared between arbitrarily many parties. In order for two qubits ''A'' and ''B'' to be maximally entangled, they must not be entangled with any third qubit ''C'' whatsoever. Even if ''A'' and ''B'' are not maximally entangled, the degree of entanglement between them constrains the degree to which either can be entangled with ''C''. In full generality, for n \geq 3 qubits A_1, \ldots, A_n, monogamy is characterized by the Coffman-Kundu-Wootters (CKW) inequality, which states that :\sum_^ \tau(\rho_) \leq \tau(\rho_) where \rho_ is the density matrix of the substate consisting of qubits A_1 and A_k and \tau is the "tangle," a quantification of bipartite entanglement equal to the square of the concurrence. Monogamy, which is closely related to the no-cloning property, is purely a feature of quantum correlations, and has no classical analogue. Supposing that two c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Physics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary ( macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Entanglement
Quantum entanglement is the phenomenon that occurs when a group of particles are generated, interact, or share spatial proximity in a way such that the quantum state of each particle of the group cannot be described independently of the state of the others, including when the particles are separated by a large distance. The topic of quantum entanglement is at the heart of the disparity between classical and quantum physics: entanglement is a primary feature of quantum mechanics not present in classical mechanics. Measurements of physical properties such as position, momentum, spin, and polarization performed on entangled particles can, in some cases, be found to be perfectly correlated. For example, if a pair of entangled particles is generated such that their total spin is known to be zero, and one particle is found to have clockwise spin on a first axis, then the spin of the other particle, measured on the same axis, is found to be anticlockwise. However, this behavior gives ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density Matrix
In quantum mechanics, a density matrix (or density operator) is a matrix that describes the quantum state of a physical system. It allows for the calculation of the probabilities of the outcomes of any measurement performed upon this system, using the Born rule. It is a generalization of the more usual state vectors or wavefunctions: while those can only represent pure states, density matrices can also represent ''mixed states''. Mixed states arise in quantum mechanics in two different situations: first when the preparation of the system is not fully known, and thus one must deal with a statistical ensemble of possible preparations, and second when one wants to describe a physical system which is entangled with another, without describing their combined state. Density matrices are thus crucial tools in areas of quantum mechanics that deal with mixed states, such as quantum statistical mechanics, open quantum systems, quantum decoherence, and quantum information. Definition ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Concurrence (quantum Computing)
In quantum information science, the concurrence is a state invariant involving qubits. Definition The concurrence is an entanglement monotone (a way of measuring entanglement) defined for a mixed state of two qubits as: : \mathcal(\rho)\equiv\max(0,\lambda_1-\lambda_2-\lambda_3-\lambda_4) in which \lambda_1,...,\lambda_4 are the eigenvalues, in decreasing order, of the Hermitian matrix :R = \sqrt with :\tilde = (\sigma_\otimes\sigma_)\rho^(\sigma_\otimes\sigma_) the spin-flipped state of \rho and \sigma_y a Pauli spin matrix. The complex conjugation ^* is taken in the eigenbasis of the Pauli matrix \sigma_z. Also, here, for a positive semidefinite matrix A, \sqrt denotes a positive semidefinite matrix B such that B^2=A. Note that B is a unique matrix so defined. A generalized version of concurrence for multiparticle pure states in arbitrary dimensions (including the case of continuous-variables in infinite dimensions) is defined as: : \mathcal_(\rho)=\sqrt in which \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
No-cloning Theorem
In physics, the no-cloning theorem states that it is impossible to create an independent and identical copy of an arbitrary unknown quantum state, a statement which has profound implications in the field of quantum computing among others. The theorem is an evolution of the 1970 no-go theorem authored by James Park, in which he demonstrates that a non-disturbing measurement scheme which is both simple and perfect cannot exist (the same result would be independently derived in 1982 by Wootters and Zurek as well as Dieks the same year). The aforementioned theorems do not preclude the state of one system becoming entangled with the state of another as cloning specifically refers to the creation of a separable state with identical factors. For example, one might use the controlled NOT gate and the Walsh–Hadamard gate to entangle two qubits without violating the no-cloning theorem as no well-defined state may be defined in terms of a subsystem of an entangled state. The no-cloning ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary ( macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Firewall (physics)
A black hole firewall is a hypothetical phenomenon where an observer falling into a black hole encounters high-energy quanta at (or near) the event horizon. The "firewall" phenomenon was proposed in 2012 by physicists Ahmed Almheiri, Donald Marolf, Joseph Polchinski, and James Sully as a possible solution to an apparent inconsistency in black hole complementarity. The proposal is sometimes referred to as the AMPS firewall, an initialism for the names of the authors of the 2012 paper. The potential inconsistency pointed out by AMPS had been pointed out earlier by Samir Mathur who used the argument in favour of the fuzzball proposal. The use of a firewall to resolve this inconsistency remains controversial, with physicists divided as to the solution to the paradox. The motivating paradox According to quantum field theory in curved spacetime, a single emission of Hawking radiation involves two mutually entangled particles. The outgoing particle escapes and is emitted as a qua ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Cryptography
Quantum cryptography is the science of exploiting quantum mechanical properties to perform cryptographic tasks. The best known example of quantum cryptography is quantum key distribution which offers an information-theoretically secure solution to the key exchange problem. The advantage of quantum cryptography lies in the fact that it allows the completion of various cryptographic tasks that are proven or conjectured to be impossible using only classical (i.e. non-quantum) communication. For example, it is impossible to copy data encoded in a quantum state. If one attempts to read the encoded data, the quantum state will be changed due to wave function collapse (no-cloning theorem). This could be used to detect eavesdropping in quantum key distribution (QKD). History In the early 1970s, Stephen Wiesner, then at Columbia University in New York, introduced the concept of quantum conjugate coding. His seminal paper titled "Conjugate Coding" was rejected by the IEEE Informati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Key Distribution
Quantum key distribution (QKD) is a secure communication method which implements a cryptographic protocol involving components of quantum mechanics. It enables two parties to produce a shared random secret key known only to them, which can then be used to encrypt and decrypt messages. It is often incorrectly called quantum cryptography, as it is the best-known example of a quantum cryptographic task. An important and unique property of quantum key distribution is the ability of the two communicating users to detect the presence of any third party trying to gain knowledge of the key. This results from a fundamental aspect of quantum mechanics: the process of measuring a quantum system in general disturbs the system. A third party trying to eavesdrop on the key must in some way measure it, thus introducing detectable anomalies. By using quantum superpositions or quantum entanglement and transmitting information in quantum states, a communication system can be implemented that dete ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
William Wootters
William "Bill" Kent Wootters () is an American theoretical physicist, and one of the founders of the field of quantum information theory. In a 1982 joint paper with Wojciech H. Zurek, Wootters proved the no cloning theorem, at the same time as Dennis Dieks, and independently of James L. Park who had formulated the no-cloning theorem in 1970. He is known for his contributions to the theory of quantum entanglement including quantitative measures of it, entanglement-assisted communication (notably quantum teleportation, discovered by Wootters and collaborators in 1993) and entanglement distillation. The term ''qubit,'' denoting the basic unit of quantum information, originated in a conversation between Wootters and Benjamin Schumacher in 1992. He earned a B.S. from Stanford University in 1973, and his Ph.D. from the University of Texas at Austin in 1980. His thesis was titled ''The Acquisition of Information from Quantum Measurements,'' and Linda Reichl was his doctoral advi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
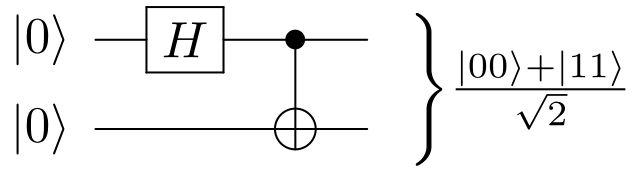
Bell State
The Bell states or EPR pairs are specific quantum states of two qubits that represent the simplest (and maximal) examples of quantum entanglement; conceptually, they fall under the study of quantum information science. The Bell states are a form of entangled and normalized basis vectors. This normalization implies that the overall probability of the particle being in one of the mentioned states is 1: \langle \Phi, \Phi \rangle = 1. Entanglement is a basis-independent result of superposition. Due to this superposition, measurement of the qubit will " collapse" it into one of its basis states with a given probability. Because of the entanglement, measurement of one qubit will "collapse" the other qubit to a state whose measurement will yield one of two possible values, where the value depends on which Bell state the two qubits are in initially. Bell states can be generalized to certain quantum states of multi-qubit systems, such as the GHZ state for 3 or more subsystems. Under ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |