|
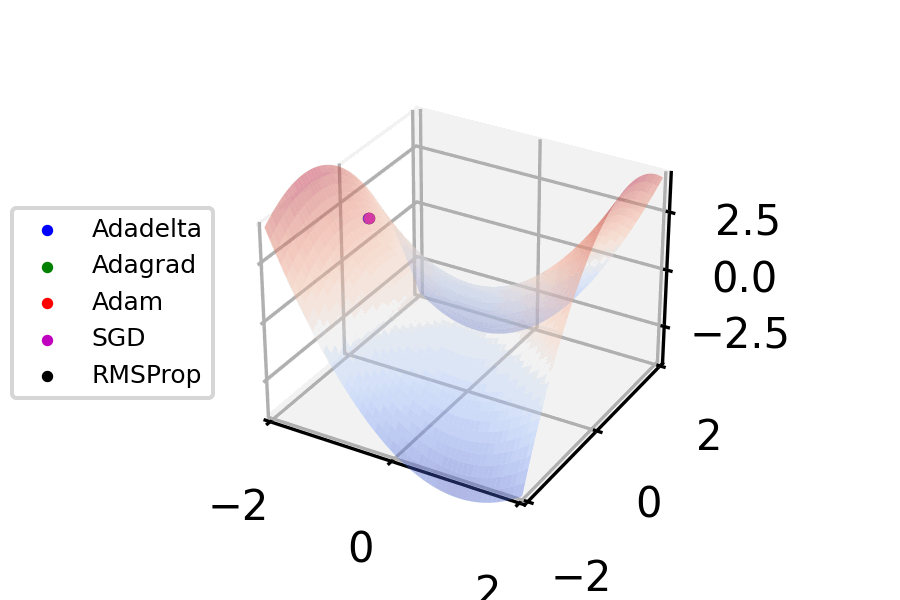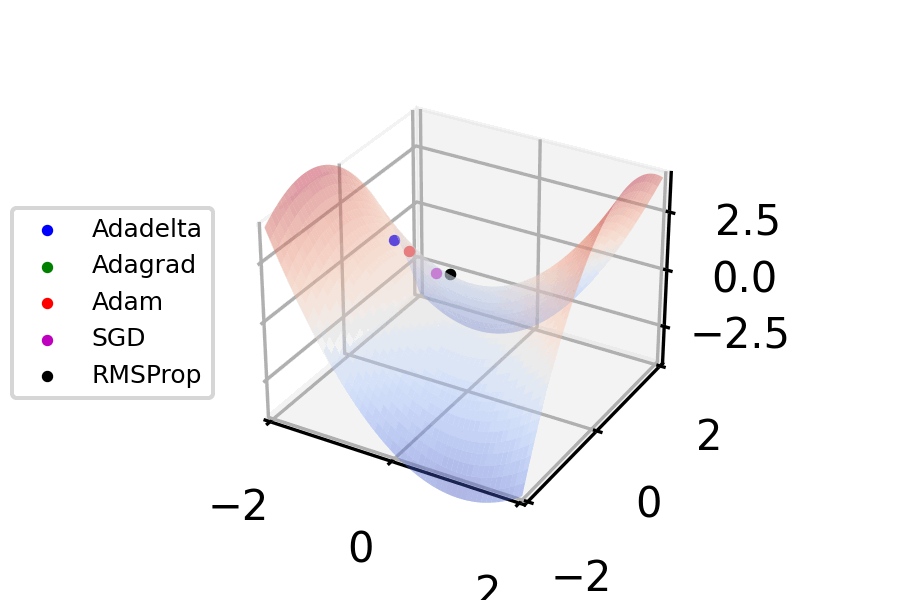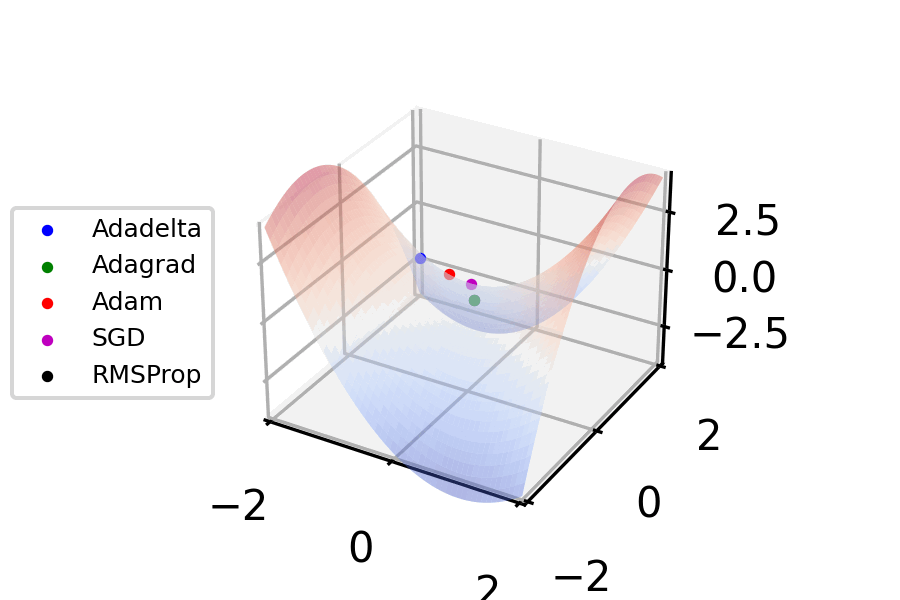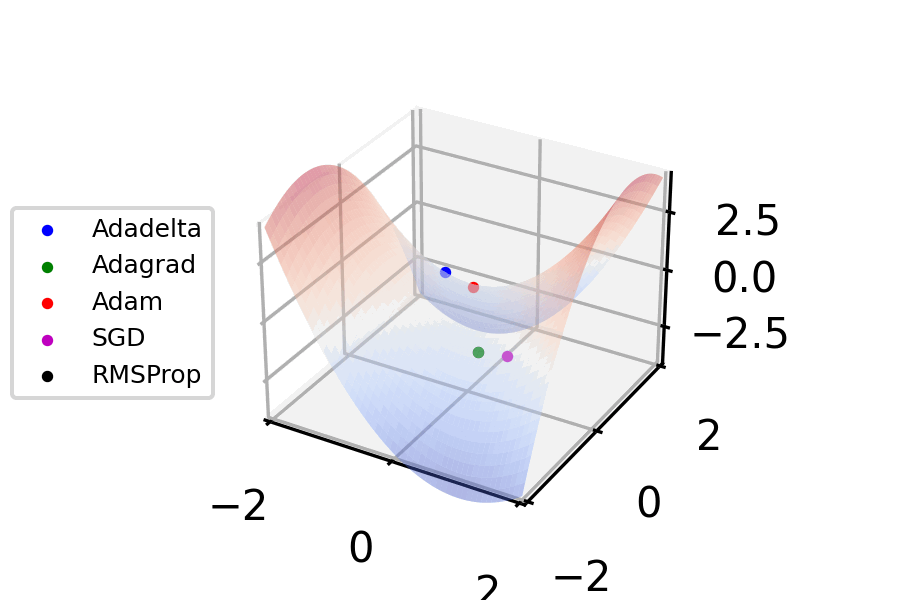
Momentum Gradient Descent
Stochastic gradient descent (often abbreviated SGD) is an iterative method for optimizing an objective function with suitable smoothness properties (e.g. differentiable or subdifferentiable). It can be regarded as a stochastic approximation of gradient descent optimization, since it replaces the actual gradient (calculated from the entire data set) by an estimate thereof (calculated from a randomly selected subset of the data). Especially in high-dimensional optimization problems this reduces the very high computational burden, achieving faster iterations in exchange for a lower convergence rate. The basic idea behind stochastic approximation can be traced back to the Robbins–Monro algorithm of the 1950s. Today, stochastic gradient descent has become an important optimization method in machine learning. Background Both statistical estimation and machine learning consider the problem of minimizing an objective function that has the form of a sum: Q(w) = \frac\sum_^n Q_i(w), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Iterative Method
In computational mathematics, an iterative method is a Algorithm, mathematical procedure that uses an initial value to generate a sequence of improving approximate solutions for a class of problems, in which the ''i''-th approximation (called an "iterate") is derived from the previous ones. A specific implementation with Algorithm#Termination, termination criteria for a given iterative method like gradient descent, hill climbing, Newton's method, or Quasi-Newton method, quasi-Newton methods like Broyden–Fletcher–Goldfarb–Shanno algorithm, BFGS, is an algorithm of an iterative method or a method of successive approximation. An iterative method is called ''Convergent series, convergent'' if the corresponding sequence converges for given initial approximations. A mathematically rigorous convergence analysis of an iterative method is usually performed; however, heuristic-based iterative methods are also common. In contrast, direct methods attempt to solve the problem by a finit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Observation (statistics)
In statistics, a unit of observation is the unit described by the data that one analyzes. A study may treat groups as a unit of observation with a country as the unit of analysis, drawing conclusions on group characteristics from data collected at the national level. For example, in a study of the demand for money, the unit of observation might be chosen as the individual, with different observations (data points) for a given point in time differing as to which individual they refer to; or the unit of observation might be the country, with different observations differing only in regard to the country they refer to. Unit of observation vs unit of analysis The unit of observation should not be confused with the unit of analysis. A study may have a differing unit of observation and unit of analysis: for example, in community research, the research design may collect data at the individual level of observation but the level of analysis might be at the neighborhood level, drawing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Advances In Neural Information Processing Systems
The Conference and Workshop on Neural Information Processing Systems (abbreviated as NeurIPS and formerly NIPS) is a machine learning and computational neuroscience Academic conference, conference held every December. Along with International Conference on Learning Representations, ICLR and International Conference on Machine Learning, ICML, it is one of the three primary conferences of high impact in machine learning and artificial intelligence research. The conference is currently a double-track meeting (single-track until 2015) that includes invited talks as well as oral and poster presentations of refereed papers, followed by parallel-track workshops that up to 2013 were held at ski resorts. History The NeurIPS meeting was first proposed in 1986 at the annual invitation-only Snowbird Meeting on Artificial neural network, Neural Networks for Computing organized by The California Institute of Technology and Bell Laboratories. NeurIPS was designed as a complementary open in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sampling (statistics)
In this statistics, quality assurance, and survey methodology, sampling is the selection of a subset or a statistical sample (termed sample for short) of individuals from within a population (statistics), statistical population to estimate characteristics of the whole population. The subset is meant to reflect the whole population, and statisticians attempt to collect samples that are representative of the population. Sampling has lower costs and faster data collection compared to recording data from the entire population (in many cases, collecting the whole population is impossible, like getting sizes of all stars in the universe), and thus, it can provide insights in cases where it is infeasible to measure an entire population. Each observation measures one or more properties (such as weight, location, colour or mass) of independent objects or individuals. In survey sampling, weights can be applied to the data to adjust for the sample design, particularly in stratified samplin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Families
In probability and statistics, an exponential family is a parametric set of probability distributions of a certain form, specified below. This special form is chosen for mathematical convenience, including the enabling of the user to calculate expectations, covariances using differentiation based on some useful algebraic properties, as well as for generality, as exponential families are in a sense very natural sets of distributions to consider. The term exponential class is sometimes used in place of "exponential family", or the older term Koopman–Darmois family. Sometimes loosely referred to as ''the'' exponential family, this class of distributions is distinct because they all possess a variety of desirable properties, most importantly the existence of a sufficient statistic. The concept of exponential families is credited to E. J. G. Pitman, G. Darmois, and B. O. Koopman in 1935–1936. Exponential families of distributions provide a general framework for selecting ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Learning Rate
In machine learning and statistics, the learning rate is a tuning parameter in an optimization algorithm that determines the step size at each iteration while moving toward a minimum of a loss function. Since it influences to what extent newly acquired information overrides old information, it metaphorically represents the speed at which a machine learning model "learns". In the adaptive control literature, the learning rate is commonly referred to as gain. In setting a learning rate, there is a trade-off between the rate of convergence and overshooting. While the descent direction is usually determined from the gradient of the loss function, the learning rate determines how big a step is taken in that direction. A too high learning rate will make the learning jump over minima but a too low learning rate will either take too long to converge or get stuck in an undesirable local minimum. In order to achieve faster convergence, prevent oscillations and getting stuck in undesi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
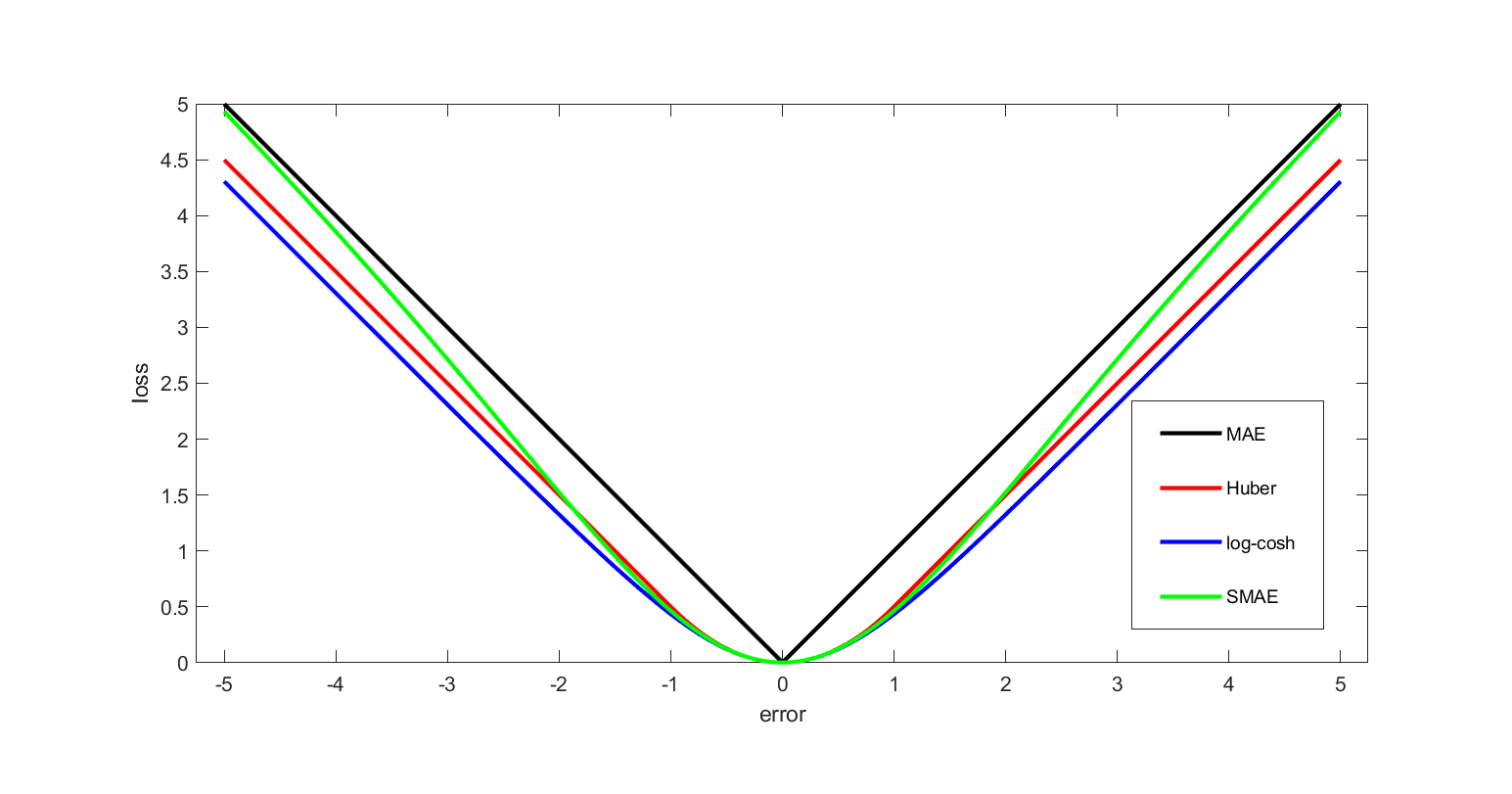
Loss Function
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite (in specific domains, variously called a reward function, a profit function, a utility function, a fitness function, etc.), in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy. In statistics, typically a loss function is used for parameter estimation, and the event in question is some function of the difference between estimated and true values for an instance of data. The concept, as old as Pierre-Simon Laplace, Laplace, was reintroduced in statistics by Abraham Wald in the middle of the 20th century. In the context of economi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Empirical Risk Minimization
In statistical learning theory, the principle of empirical risk minimization defines a family of learning algorithms based on evaluating performance over a known and fixed dataset. The core idea is based on an application of the law of large numbers; more specifically, we cannot know exactly how well a predictive algorithm will work in practice (i.e. the "true risk") because we do not know the true distribution of the data, but we can instead estimate and optimize the performance of the algorithm on a known set of training data. The performance over the known set of training data is referred to as the "empirical risk". Background The following situation is a general setting of many supervised learning problems. There are two spaces of objects X and Y and we would like to learn a function \ h: X \to Y (often called ''hypothesis'') which outputs an object y \in Y, given x \in X. To do so, there is a ''training set'' of n examples \ (x_1, y_1), \ldots, (x_n, y_n) where x_i \in X ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Estimating Equations
In statistics, the method of estimating equations is a way of specifying how the parameters of a statistical model should be estimated. This can be thought of as a generalisation of many classical methods—the method of moments, least squares, and maximum likelihood—as well as some recent methods like M-estimators. The basis of the method is to have, or to find, a set of simultaneous equations involving both the sample data and the unknown model parameters which are to be solved in order to define the estimates of the parameters. Various components of the equations are defined in terms of the set of observed data on which the estimates are to be based. Important examples of estimating equations are the likelihood equations. Examples Consider the problem of estimating the rate parameter, λ of the exponential distribution which has the probability density function: : f(x;\lambda) = \left\{\begin{matrix} \lambda e^{-\lambda x}, &\; x \ge 0, \\ 0, &\; x < 0. \end{m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Score (statistics)
In statistics, the score (or informant) is the gradient of the log-likelihood function with respect to the statistical parameter, parameter vector. Evaluated at a particular value of the parameter vector, the score indicates the steepness of the log-likelihood function and thereby the sensitivity to infinitesimal changes to the parameter values. If the log-likelihood function is Continuous function, continuous over the parameter space, the score will vanish (mathematics), vanish at a local Maxima and minima, maximum or minimum; this fact is used in maximum likelihood estimation to find the parameter values that maximize the likelihood function. Since the score is a function of the Realization (probability), observations, which are subject to sampling error, it lends itself to a test statistic known as ''score test'' in which the parameter is held at a particular value. Further, the likelihood ratio, ratio of two likelihood functions evaluated at two distinct parameter values can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Likelihood Function
A likelihood function (often simply called the likelihood) measures how well a statistical model explains observed data by calculating the probability of seeing that data under different parameter values of the model. It is constructed from the joint probability distribution of the random variable that (presumably) generated the observations. When evaluated on the actual data points, it becomes a function solely of the model parameters. In maximum likelihood estimation, the argument that maximizes the likelihood function serves as a point estimate for the unknown parameter, while the Fisher information (often approximated by the likelihood's Hessian matrix at the maximum) gives an indication of the estimate's precision. In contrast, in Bayesian statistics, the estimate of interest is the ''converse'' of the likelihood, the so-called posterior probability of the parameter given the observed data, which is calculated via Bayes' rule. Definition The likelihood function, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stationary Point
In mathematics, particularly in calculus, a stationary point of a differentiable function of one variable is a point on the graph of a function, graph of the function where the function's derivative is zero. Informally, it is a point where the function "stops" increasing or decreasing (hence the name). For a differentiable function of several real variables, a stationary point is a point on the surface (mathematics), surface of the graph where all its partial derivatives are zero (equivalently, the gradient has zero vector norm, norm). The notion of stationary points of a real-valued function is generalized as ''Critical point (mathematics), critical points'' for complex-valued functions. Stationary points are easy to visualize on the graph of a function of one variable: they correspond to the points on the graph where the tangent is horizontal (i.e., Parallel (geometry), parallel to the Abscissa, -axis). For a function of two variables, they correspond to the points on the gr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |