|
Method Of Moving Frames
In mathematics, a moving frame is a flexible generalization of the notion of a coordinate frame (an ordered basis of a vector space, in conjunction with an origin) often used to study the extrinsic differential geometry of smooth manifolds embedded in a homogeneous space. Introduction In lay terms, a ''frame of reference'' is a system of measuring rods used by an observer to measure the surrounding space by providing coordinates. A moving frame is then a frame of reference which moves with the observer along a trajectory (a curve). The method of the moving frame, in this simple example, seeks to produce a "preferred" moving frame out of the kinematic properties of the observer. In a geometrical setting, this problem was solved in the mid 19th century by Jean Frédéric Frenet and Joseph Alfred Serret. The Frenet–Serret frame is a moving frame defined on a curve which can be constructed purely from the velocity and acceleration of the curve. The Frenet–Serret frame pl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Joseph Alfred Serret
Joseph-Alfred Serret (; August 30, 1819 – March 2, 1885) was a French mathematician who was born in Paris, France, and died in Versailles, France. See also *Frenet–Serret formulas In differential geometry, the Frenet–Serret formulas describe the kinematic properties of a particle moving along a differentiable curve in three-dimensional Euclidean space \R^3, or the geometric properties of the curve itself irrespective o ... Books by J.-A. Serret Traité de trigonométrie(Gautier-Villars, 1880) Cours de calcul differentiel et integral t. 1(Gauthier-Villars, 1900) Cours de calcul differentiel et integral t. 2(Gauthier-Villars, 1900) Cours d'algèbre supérieure. Tome I(Gauthier-Villars, 1877) Cours d'algèbre supérieure. Tome II(Gauthier-Villars, 1879) External links * * 1819 births 1885 deaths 19th-century French mathematicians École Polytechnique alumni Members of the French Academy of Sciences Differential geometers {{France-mathematician-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integrability Conditions For Differential Systems
In mathematics, certain systems of partial differential equations are usefully formulated, from the point of view of their underlying geometric and algebraic structure, in terms of a system of differential forms. The idea is to take advantage of the way a differential form ''restricts'' to a submanifold, and the fact that this restriction is compatible with the exterior derivative. This is one possible approach to certain over-determined systems, for example, including Lax pairs of integrable systems. A Pfaffian system is specified by 1-forms alone, but the theory includes other types of example of differential system. To elaborate, a Pfaffian system is a set of 1-forms on a smooth manifold (which one sets equal to 0 to find ''solutions'' to the system). Given a collection of differential 1-forms \textstyle\alpha_i, i=1,2,\dots, k on an \textstyle n-dimensional manifold , an integral manifold is an immersed (not necessarily embedded) submanifold whose tangent space at every poi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Darboux Frame
In the differential geometry of surfaces, a Darboux frame is a natural moving frame constructed on a surface. It is the analog of the Frenet–Serret frame as applied to surface geometry. A Darboux frame exists at any non- umbilic point of a surface embedded in Euclidean space. It is named after French mathematician Jean Gaston Darboux. Darboux frame of an embedded curve Let ''S'' be an oriented surface in three-dimensional Euclidean space E3. The construction of Darboux frames on ''S'' first considers frames moving along a curve in ''S'', and then specializes when the curves move in the direction of the principal curvatures. Definition At each point of an oriented surface, one may attach a unit normal vector in a unique way, as soon as an orientation has been chosen for the normal at any particular fixed point. If is a curve in , parametrized by arc length, then the Darboux frame of is defined by : \mathbf(s) = \gamma'(s), (the ''unit tangent'') : \ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface (mathematics)
In mathematics, a surface is a mathematical model of the common concept of a surface. It is a generalization of a plane, but, unlike a plane, it may be curved; this is analogous to a curve generalizing a straight line. There are several more precise definitions, depending on the context and the mathematical tools that are used for the study. The simplest mathematical surfaces are planes and spheres in the Euclidean 3-space. The exact definition of a surface may depend on the context. Typically, in algebraic geometry, a surface may cross itself (and may have other singularities), while, in topology and differential geometry, it may not. A surface is a topological space of dimension two; this means that a moving point on a surface may move in two directions (it has two degrees of freedom). In other words, around almost every point, there is a '' coordinate patch'' on which a two-dimensional coordinate system is defined. For example, the surface of the Earth resembles ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaston Darboux
Jean-Gaston Darboux FAS MIF FRS FRSE (14 August 1842 – 23 February 1917) was a French mathematician. Life According to his birth certificate, he was born in Nîmes in France on 14 August 1842, at 1 am. However, probably due to the midnight birth, Darboux himself usually reported his own birthday as 13 August, ''e.g.'' in his filled form for Légion d'Honneur. His parents were François Darboux, businessman of mercery, and Alix Gourdoux. The father died when Gaston was 7. His mother undertook the mercery business with great courage, and insisted that her children receive good education. Gaston had a younger brother, Louis, who taught mathematics at the Lycée Nîmes for almost his entire life. He studied at the Nîmes Lycée and the Montpellier Lycée before being accepted as the top qualifier at the École normale supérieure in 1861, and received his PhD there in 1866. His thesis, written under the direction of Michel Chasles, was titled ''Sur les surfaces orthogonal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Darboux Trihedron
Darboux is a surname. Notable people with the surname include: * Jean Gaston Darboux (1842–1917), French mathematician * Lauriane Doumbouya (née Darboux), the current First Lady of Guinea since 5 September 2021 * Paul Darboux (1919–1982), Beninese politician {{surname ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable. The process of finding a derivative is called differentiation. There are multiple different notations for differentiation. '' Leibniz notation'', named after Gottfried Wilhelm Leibniz, is represented as the ratio of two differentials, whereas ''prime notation'' is written by adding a prime mark. Higher order notations represent repeated differentiation, and they are usually denoted in Leib ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
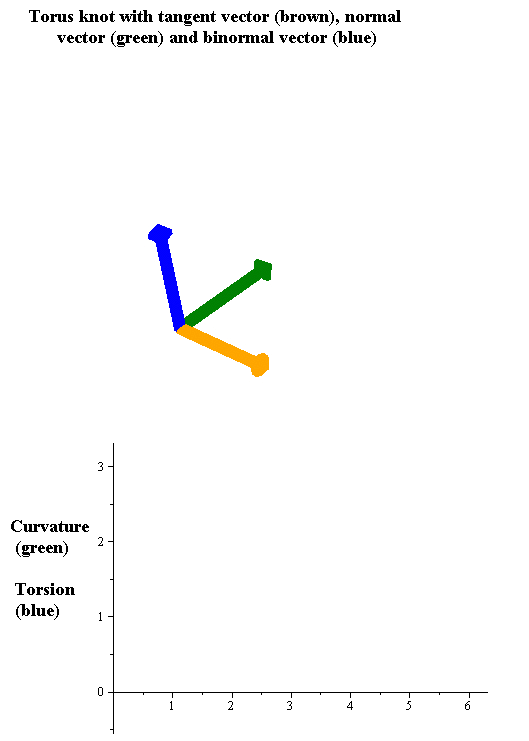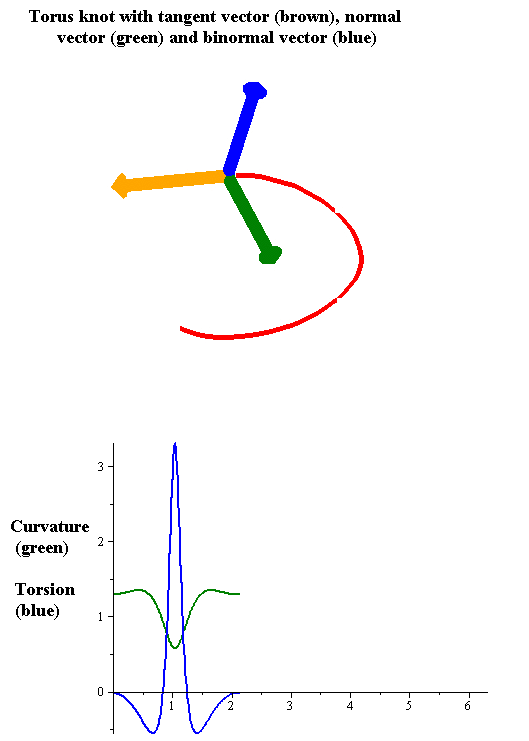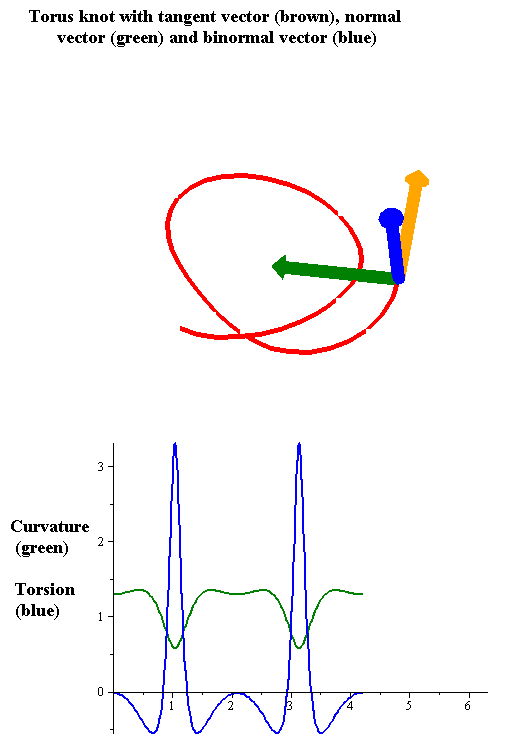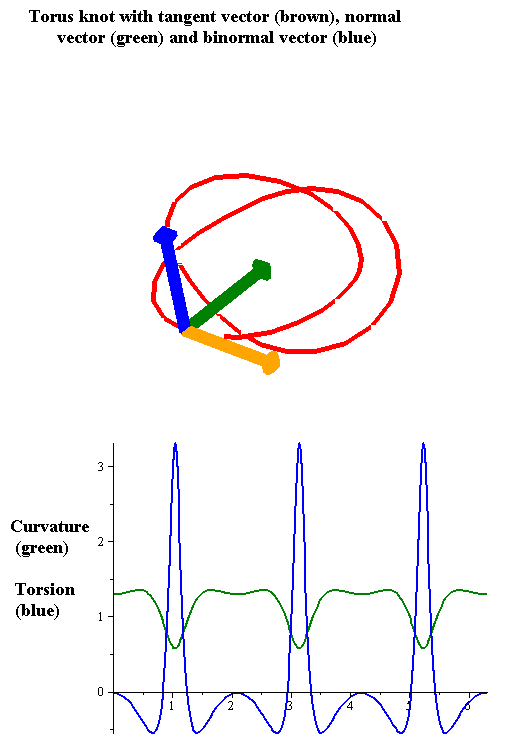
Curvature
In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. If a curve or surface is contained in a larger space, curvature can be defined ''extrinsically'' relative to the ambient space. Curvature of Riemannian manifolds of dimension at least two can be defined ''intrinsically'' without reference to a larger space. For curves, the canonical example is that of a circle, which has a curvature equal to the reciprocal of its radius. Smaller circles bend more sharply, and hence have higher curvature. The curvature ''at a point'' of a differentiable curve is the curvature of its osculating circle — that is, the circle that best approximates the curve near this point. The curvature of a straight line is zero. In contrast to the tangent, which is a vector quantity, the curvature at a point is typically a scalar q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torsion Of A Curve
In the differential geometry of curves in three dimensions, the torsion of a curve measures how sharply it is twisting out of the osculating plane. Taken together, the curvature and the torsion of a space curve are analogous to the curvature of a plane curve. For example, they are coefficients in the system of differential equations for the Frenet frame given by the Frenet–Serret formulas. Definition Let be a space curve parametrized by arc length and with the unit tangent vector . If the curvature of at a certain point is not zero then the principal normal vector and the binormal vector at that point are the unit vectors : \mathbf=\frac, \quad \mathbf=\mathbf\times\mathbf respectively, where the prime denotes the derivative of the vector with respect to the parameter . The torsion measures the speed of rotation of the binormal vector at the given point. It is found from the equation : \mathbf' = -\tau\mathbf. which means : \tau = -\mathbf\cdot\math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Congruence (geometry)
In geometry, two figures or objects are congruent if they have the same shape and size, or if one has the same shape and size as the mirror image of the other. More formally, two sets of points are called congruent if, and only if, one can be transformed into the other by an isometry, i.e., a combination of rigid motions, namely a translation, a rotation, and a reflection. This means that either object can be repositioned and reflected (but not resized) so as to coincide precisely with the other object. Therefore, two distinct plane figures on a piece of paper are congruent if they can be cut out and then matched up completely. Turning the paper over is permitted. In elementary geometry the word ''congruent'' is often used as follows. The word ''equal'' is often used in place of ''congruent'' for these objects. *Two line segments are congruent if they have the same length. *Two angles are congruent if they have the same measure. *Two circles are congruent if they have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Geometry Of Curves
Differential geometry of curves is the branch of geometry that deals with smooth curves in the plane and the Euclidean space by methods of differential and integral calculus. Many specific curves have been thoroughly investigated using the synthetic approach. Differential geometry takes another path: curves are represented in a parametrized form, and their geometric properties and various quantities associated with them, such as the curvature and the arc length, are expressed via derivatives and integrals using vector calculus. One of the most important tools used to analyze a curve is the Frenet frame, a moving frame that provides a coordinate system at each point of the curve that is "best adapted" to the curve near that point. The theory of curves is much simpler and narrower in scope than the theory of surfaces and its higher-dimensional generalizations because a regular curve in a Euclidean space has no intrinsic geometry. Any regular curve may be parametrized by th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |