|
Maximum Entropy Classifier
In statistics, multinomial logistic regression is a classification method that generalizes logistic regression to multiclass problems, i.e. with more than two possible discrete outcomes. That is, it is a model that is used to predict the probabilities of the different possible outcomes of a categorically distributed dependent variable, given a set of independent variables (which may be real-valued, binary-valued, categorical-valued, etc.). Multinomial logistic regression is known by a variety of other names, including polytomous LR, multiclass LR, softmax regression, multinomial logit (mlogit), the maximum entropy (MaxEnt) classifier, and the conditional maximum entropy model. Background Multinomial logistic regression is used when the dependent variable in question is nominal (equivalently ''categorical'', meaning that it falls into any one of a set of categories that cannot be ordered in any meaningful way) and for which there are more than two categories. Some examples ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Predictor Function
In statistics and in machine learning, a linear predictor function is a linear function ( linear combination) of a set of coefficients and explanatory variables (independent variables), whose value is used to predict the outcome of a dependent variable. This sort of function usually comes in linear regression, where the coefficients are called regression coefficients. However, they also occur in various types of linear classifiers (e.g. logistic regression, perceptrons,Rosenblatt, Frank (1957), The Perceptron--a perceiving and recognizing automaton. Report 85-460-1, Cornell Aeronautical Laboratory. support vector machines, and linear discriminant analysis), as well as in various other models, such as principal component analysisJolliffe I.T. ''Principal Component Analysis'', Series: Springer Series in Statistics, 2nd ed., Springer, NY, 2002, XXIX, 487 p. 28 illus. and factor analysis. In many of these models, the coefficients are referred to as "weights". Definition The ba ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Variable
Binary data is data whose unit can take on only two possible states. These are often labelled as 0 and 1 in accordance with the binary numeral system and Boolean algebra. Binary data occurs in many different technical and scientific fields, where it can be called by different names including ''bit'' (binary digit) in computer science, ''truth value'' in mathematical logic and related domains and '' binary variable'' in statistics. Mathematical and combinatoric foundations A discrete variable that can take only one state contains zero information, and is the next natural number after 1. That is why the bit, a variable with only two possible values, is a standard primary unit of information. A collection of bits may have states: see binary number for details. Number of states of a collection of discrete variables depends exponentially on the number of variables, and only as a power law on number of states of each variable. Ten bits have more () states than three decimal di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Categorical Variable
In statistics, a categorical variable (also called qualitative variable) is a variable that can take on one of a limited, and usually fixed, number of possible values, assigning each individual or other unit of observation to a particular group or nominal category on the basis of some qualitative property. In computer science and some branches of mathematics, categorical variables are referred to as enumerations or enumerated types. Commonly (though not in this article), each of the possible values of a categorical variable is referred to as a level. The probability distribution associated with a random categorical variable is called a categorical distribution. Categorical data is the statistical data type consisting of categorical variables or of data that has been converted into that form, for example as grouped data. More specifically, categorical data may derive from observations made of qualitative data that are summarised as counts or cross tabulations, or from observ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Error Propagation
In statistics, propagation of uncertainty (or propagation of error) is the effect of variables' uncertainties (or errors, more specifically random errors) on the uncertainty of a function based on them. When the variables are the values of experimental measurements they have uncertainties due to measurement limitations (e.g., instrument precision) which propagate due to the combination of variables in the function. The uncertainty ''u'' can be expressed in a number of ways. It may be defined by the absolute error . Uncertainties can also be defined by the relative error , which is usually written as a percentage. Most commonly, the uncertainty on a quantity is quantified in terms of the standard deviation, , which is the positive square root of the variance. The value of a quantity and its error are then expressed as an interval . If the statistical probability distribution of the variable is known or can be assumed, it is possible to derive confidence limits to descri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Predictive Modelling
Predictive modelling uses statistics to predict outcomes. Most often the event one wants to predict is in the future, but predictive modelling can be applied to any type of unknown event, regardless of when it occurred. For example, predictive models are often used to detect crimes and identify suspects, after the crime has taken place. In many cases the model is chosen on the basis of detection theory to try to guess the probability of an outcome given a set amount of input data, for example given an email determining how likely that it is spam. Models can use one or more classifiers in trying to determine the probability of a set of data belonging to another set. For example, a model might be used to determine whether an email is spam or "ham" (non-spam). Depending on definitional boundaries, predictive modelling is synonymous with, or largely overlapping with, the field of machine learning, as it is more commonly referred to in academic or research and development contexts. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability
Probability is the branch of mathematics concerning numerical descriptions of how likely an Event (probability theory), event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and 1, where, roughly speaking, 0 indicates impossibility of the event and 1 indicates certainty."Kendall's Advanced Theory of Statistics, Volume 1: Distribution Theory", Alan Stuart and Keith Ord, 6th Ed, (2009), .William Feller, ''An Introduction to Probability Theory and Its Applications'', (Vol 1), 3rd Ed, (1968), Wiley, . The higher the probability of an event, the more likely it is that the event will occur. A simple example is the tossing of a fair (unbiased) coin. Since the coin is fair, the two outcomes ("heads" and "tails") are both equally probable; the probability of "heads" equals the probability of "tails"; and since no other outcomes are possible, the probability of either "heads" or "tails" is 1/2 (which could also be written ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
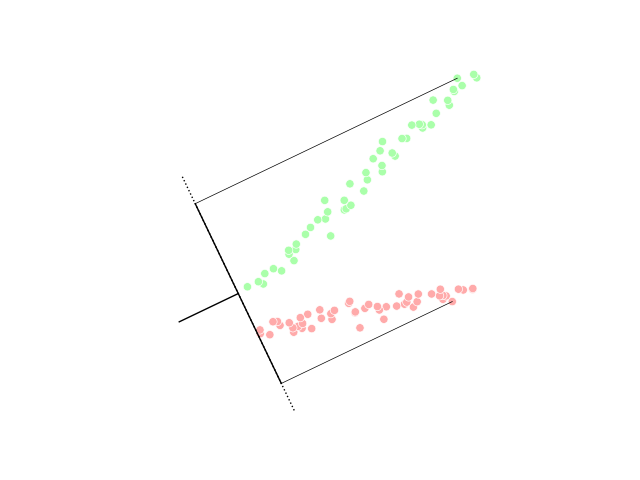
Linear Discriminant Analysis
Linear discriminant analysis (LDA), normal discriminant analysis (NDA), or discriminant function analysis is a generalization of Fisher's linear discriminant, a method used in statistics and other fields, to find a linear combination of features that characterizes or separates two or more classes of objects or events. The resulting combination may be used as a linear classifier, or, more commonly, for dimensionality reduction before later classification. LDA is closely related to analysis of variance (ANOVA) and regression analysis, which also attempt to express one dependent variable as a linear combination of other features or measurements. However, ANOVA uses categorical independent variables and a continuous dependent variable, whereas discriminant analysis has continuous independent variables and a categorical dependent variable (''i.e.'' the class label). Logistic regression and probit regression are more similar to LDA than ANOVA is, as they also explain a categorica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Support Vector Machine
In machine learning, support vector machines (SVMs, also support vector networks) are supervised learning models with associated learning algorithms that analyze data for classification and regression analysis. Developed at AT&T Bell Laboratories by Vladimir Vapnik with colleagues (Boser et al., 1992, Guyon et al., 1993, Cortes and Vapnik, 1995, Vapnik et al., 1997) SVMs are one of the most robust prediction methods, being based on statistical learning frameworks or VC theory proposed by Vapnik (1982, 1995) and Chervonenkis (1974). Given a set of training examples, each marked as belonging to one of two categories, an SVM training algorithm builds a model that assigns new examples to one category or the other, making it a non-probabilistic binary linear classifier (although methods such as Platt scaling exist to use SVM in a probabilistic classification setting). SVM maps training examples to points in space so as to maximise the width of the gap between the two categories. N ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perceptron
In machine learning, the perceptron (or McCulloch-Pitts neuron) is an algorithm for supervised classification, supervised learning of binary classification, binary classifiers. A binary classifier is a function which can decide whether or not an input, represented by a vector of numbers, belongs to some specific class. It is a type of linear classifier, i.e. a classification algorithm that makes its predictions based on a linear predictor function combining a set of Weighting, weights with the feature vector. History The perceptron was invented in 1943 by McCulloch and Pitts. The first implementation was a machine built in 1958 at the Cornell Aeronautical Laboratory by Frank Rosenblatt, funded by the United States Office of Naval Research. The perceptron was intended to be a machine, rather than a program, and while its first implementation was in software for the IBM 704, it was subsequently implemented in custom-built hardware as the "Mark 1 perceptron". This machine was de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Utility
As a topic of economics, utility is used to model worth or value. Its usage has evolved significantly over time. The term was introduced initially as a measure of pleasure or happiness as part of the theory of utilitarianism by moral philosophers such as Jeremy Bentham and John Stuart Mill. The term has been adapted and reapplied within neoclassical economics, which dominates modern economic theory, as a utility function that represents a single consumer's preference ordering over a choice set but is not comparable across consumers. This concept of utility is personal and based on choice rather than on pleasure received, and so is specified more rigorously than the original concept but makes it less useful (and controversial) for ethical decisions. Utility function Consider a set of alternatives among which a person can make a preference ordering. The utility obtained from these alternatives is an unknown function of the utilities obtained from each alternative, not the sum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Choice
In economics, discrete choice models, or qualitative choice models, describe, explain, and predict choices between two or more discrete alternatives, such as entering or not entering the labor market, or choosing between modes of transport. Such choices contrast with standard consumption models in which the quantity of each good consumed is assumed to be a continuous variable. In the continuous case, calculus methods (e.g. first-order conditions) can be used to determine the optimum amount chosen, and demand can be modeled empirically using regression analysis. On the other hand, discrete choice analysis examines situations in which the potential outcomes are discrete, such that the optimum is not characterized by standard first-order conditions. Thus, instead of examining "how much" as in problems with continuous choice variables, discrete choice analysis examines "which one". However, discrete choice analysis can also be used to examine the chosen quantity when only a few dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |