|
Maximum Disjoint Set
In computational geometry, a maximum disjoint set (MDS) is a largest set of non-overlapping geometric shapes selected from a given set of candidate shapes. Every set of non-overlapping shapes is an independent set in the intersection graph of the shapes. Therefore, the MDS problem is a special case of the maximum independent set (MIS) problem. Both problems are NP complete, but finding a MDS may be easier than finding a MIS in two respects: * For the general MIS problem, the best known exact algorithms are exponential. In some geometric intersection graphs, there are sub-exponential algorithms for finding a MDS. * The general MIS problem is hard to approximate and doesn't even have a constant-factor approximation. In some geometric intersection graphs, there are polynomial-time approximation schemes (PTAS) for finding a MDS. Finding an MDS is important in applications such as automatic label placement, VLSI circuit design, and cellular frequency division multiplexing. The MDS pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational geometry. While modern computational geometry is a recent development, it is one of the oldest fields of computing with a history stretching back to antiquity. Analysis of algorithms, Computational complexity is central to computational geometry, with great practical significance if algorithms are used on very large datasets containing tens or hundreds of millions of points. For such sets, the difference between O(''n''2) and O(''n'' log ''n'') may be the difference between days and seconds of computation. The main impetus for the development of computational geometry as a discipline was progress in computer graphics and computer-aided design and manufacturing (Computer-aided design, CAD/Compu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamic Programming
Dynamic programming is both a mathematical optimization method and a computer programming method. The method was developed by Richard Bellman in the 1950s and has found applications in numerous fields, from aerospace engineering to economics. In both contexts it refers to simplifying a complicated problem by breaking it down into simpler sub-problems in a recursive manner. While some decision problems cannot be taken apart this way, decisions that span several points in time do often break apart recursively. Likewise, in computer science, if a problem can be solved optimally by breaking it into sub-problems and then recursively finding the optimal solutions to the sub-problems, then it is said to have ''optimal substructure''. If sub-problems can be nested recursively inside larger problems, so that dynamic programming methods are applicable, then there is a relation between the value of the larger problem and the values of the sub-problems.Cormen, T. H.; Leiserson, C. E.; Rives ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete & Computational Geometry
'' Discrete & Computational Geometry'' is a peer-reviewed mathematics journal published quarterly by Springer. Founded in 1986 by Jacob E. Goodman and Richard M. Pollack, the journal publishes articles on discrete geometry and computational geometry. Abstracting and indexing The journal is indexed in: * ''Mathematical Reviews'' * ''Zentralblatt MATH'' * ''Science Citation Index'' * ''Current Contents''/Engineering, Computing and Technology Notable articles The articles by Gil Kalai with a proof of a subexponential upper bound on the diameter of a polyhedron and by Samuel Ferguson on the Kepler conjecture, both published in Discrete & Computational geometry, earned their author the Fulkerson Prize The Fulkerson Prize for outstanding papers in the area of discrete mathematics is sponsored jointly by the Mathematical Optimization Society (MOS) and the American Mathematical Society (AMS). Up to three awards of $1,500 each are presented at e .... References External link ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Local Search Algorithm
In computer science, local search is a heuristic method for solving computationally hard optimization problems. Local search can be used on problems that can be formulated as finding a solution maximizing a criterion among a number of candidate solutions. Local search algorithms move from solution to solution in the space of candidate solutions (the ''search space'') by applying local changes, until a solution deemed optimal is found or a time bound is elapsed. Local search algorithms are widely applied to numerous hard computational problems, including problems from computer science (particularly artificial intelligence), mathematics, operations research, engineering, and bioinformatics. Examples of local search algorithms are WalkSAT, the 2-opt algorithm for the Traveling Salesman Problem and the Metropolis–Hastings algorithm. Examples Some problems where local search has been applied are: # The vertex cover problem, in which a solution is a vertex cover of a graph, and th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Union Complexity
Union commonly refers to: * Trade union, an organization of workers * Union (set theory), in mathematics, a fundamental operation on sets Union may also refer to: Arts and entertainment Music * Union (band), an American rock group ** ''Union'' (Union album), 1998 * ''Union'' (Chara album), 2007 * ''Union'' (Toni Childs album), 1988 * ''Union'' (Cuff the Duke album), 2012 * ''Union'' (Paradoxical Frog album), 2011 * ''Union'', a 2001 album by Puya * ''Union'', a 2001 album by Rasa * ''Union'' (The Boxer Rebellion album), 2009 * ''Union'' (Yes album), 1991 * "Union" (Black Eyed Peas song), 2005 Other uses in arts and entertainment * ''Union'' (Star Wars), a Dark Horse comics limited series * Union, in the fictional Alliance–Union universe of C. J. Cherryh * ''Union (Horse with Two Discs)'', a bronze sculpture by Christopher Le Brun, 1999–2000 * The Union (Marvel Team), a Marvel Comics superhero team and comic series Education * Union Academy (other), t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Separator
A geometric separator is a line (or another shape) that partitions a collection of geometric shapes into two subsets, such that proportion of shapes in each subset is bounded, and the number of shapes that do not belong to any subset (i.e. the shapes intersected by the separator itself) is small. When a geometric separator exists, it can be used for building divide-and-conquer algorithms for solving various problems in computational geometry. Separators that are lines General question In 1979, Helge Tverberg raised the following question. For two positive integers ''k'', ''l'', what is the smallest number ''n''(''k'',''l'') such that, for any family of pairwise-disjoint convex objects in the plane, there exists a straight line that has at least ''k'' objects on one side and at least ''l'' on the other side? The following results are known. * Obviously, ''n''(1,1)=1. * Hope and Katchalski proved that ''n''(''k'',1) ≤ 12(''k''-1) for all ''k'' ≥ 2. * Villanger prove ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Separator
A geometric separator is a line (or another shape) that partitions a collection of geometric shapes into two subsets, such that proportion of shapes in each subset is bounded, and the number of shapes that do not belong to any subset (i.e. the shapes intersected by the separator itself) is small. When a geometric separator exists, it can be used for building divide-and-conquer algorithms for solving various problems in computational geometry. Separators that are lines General question In 1979, Helge Tverberg raised the following question. For two positive integers ''k'', ''l'', what is the smallest number ''n''(''k'',''l'') such that, for any family of pairwise-disjoint convex objects in the plane, there exists a straight line that has at least ''k'' objects on one side and at least ''l'' on the other side? The following results are known. * Obviously, ''n''(1,1)=1. * Hope and Katchalski proved that ''n''(''k'',1) ≤ 12(''k''-1) for all ''k'' ≥ 2. * Villanger prove ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadtree
A quadtree is a tree data structure in which each internal node has exactly four children. Quadtrees are the two-dimensional analog of octrees and are most often used to partition a two-dimensional space by recursively subdividing it into four quadrants or regions. The data associated with a leaf cell varies by application, but the leaf cell represents a "unit of interesting spatial information". The subdivided regions may be square or rectangular, or may have arbitrary shapes. This data structure was named a quadtree by Raphael Finkel and J.L. Bentley in 1974. A similar partitioning is also known as a ''Q-tree''. All forms of quadtrees share some common features: * They decompose space into adaptable cells * Each cell (or bucket) has a maximum capacity. When maximum capacity is reached, the bucket splits * The tree directory follows the spatial decomposition of the quadtree. A tree-pyramid (T-pyramid) is a "complete" tree; every node of the T-pyramid has four child nodes excep ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Point Quadtree
Point or points may refer to: Places * Point, Lewis, a peninsula in the Outer Hebrides, Scotland * Point, Texas, a city in Rains County, Texas, United States * Point, the NE tip and a ferry terminal of Lismore, Inner Hebrides, Scotland * Points, West Virginia, an unincorporated community in the United States Business and finance * Point (loyalty program), a type of virtual currency in common use among mercantile loyalty programs, globally *Point (mortgage), a percentage sometimes referred to as a form of pre-paid interest used to reduce interest rates in a mortgage loan * Basis point, 1/100 of one percent, denoted ''bp'', ''bps'', and ''‱'' * Percentage points, used to measure a change in percentage absolutely * Pivot point (technical analysis), a price level of significance in analysis of a financial market that is used as a predictive indicator of market movement * "Points", the term for profit sharing in the American film industry, where creatives involved in making the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pigeonhole Principle
In mathematics, the pigeonhole principle states that if items are put into containers, with , then at least one container must contain more than one item. For example, if one has three gloves (and none is ambidextrous/reversible), then there must be at least two right-handed gloves, or at least two left-handed gloves, because there are three objects, but only two categories of handedness to put them into. This seemingly obvious statement, a type of counting argument, can be used to demonstrate possibly unexpected results. For example, given that the population of London is greater than the maximum number of hairs that can be present on a human's head, then the pigeonhole principle requires that there must be at least two people in London who have the same number of hairs on their heads. Although the pigeonhole principle appears as early as 1624 in a book attributed to Jean Leurechon, it is commonly called Dirichlet's box principle or Dirichlet's drawer principle after an 1834 t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
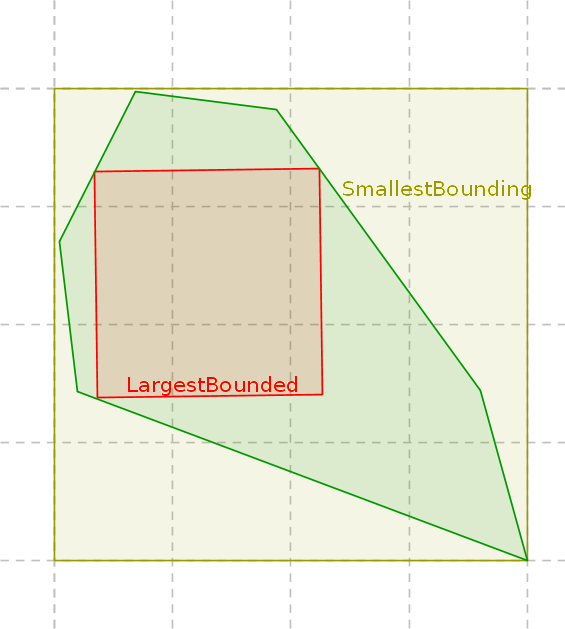
Fat Object (geometry)
In geometry, a fat object is an object in two or more dimensions, whose lengths in the different dimensions are similar. For example, a square is fat because its length and width are identical. A 2-by-1 rectangle is thinner than a square, but it is fat relative to a 10-by-1 rectangle. Similarly, a circle is fatter than a 1-by-10 ellipse and an equilateral triangle is fatter than a very obtuse triangle. Fat objects are especially important in computational geometry. Many algorithms in computational geometry can perform much better if their input consists of only fat objects; see the applications section below. Global fatness Given a constant ''R''≥1, an object ''o'' is called ''R''-fat if its "slimness factor" is at most ''R''. The "slimness factor" has different definitions in different papers. A common definition is: :\frac where ''o'' and the cubes are ''d''-dimensional. A 2-dimensional cube is a square, so the slimness factor of a square is 1 (since its smallest enclosing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circles
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant. The distance between any point of the circle and the centre is called the radius. Usually, the radius is required to be a positive number. A circle with r=0 (a single point) is a degenerate case. This article is about circles in Euclidean geometry, and, in particular, the Euclidean plane, except where otherwise noted. Specifically, a circle is a simple closed curve that divides the plane into two regions: an interior and an exterior. In everyday use, the term "circle" may be used interchangeably to refer to either the boundary of the figure, or to the whole figure including its interior; in strict technical usage, the circle is only the boundary and the whole figure is called a '' disc''. A circle may also be defined as a special ki ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
