|
Matrix Element (physics)
In physics, particularly in quantum perturbation theory, the matrix element refers to the linear operator of a modified Hamiltonian using Dirac notation. It is in fact referring to the matrix elements of a Hamiltonian operator which serves the purpose of calculating transition probabilities between different quantum states. The matrix element considers the effect of the newly modified Hamiltonian (i.e. the linear superposition of the unperturbed Hamiltonian plus interaction potential) on the quantum state. Matrix elements are important in atomic, nuclear and particle physics. In simple terms, we say that a Hamiltonian or some other operator/observable will cause a transition from an initial quantum state , i \rangle to a final quantum state , f \rangle if the following holds true:\begin \langle f , \hat , i \rangle = M^ \neq 0\\ , \langle f , \hat , i \rangle, ^2 = , M^, ^2, \end where the last line is the probability amplitude of transition caused by so ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix (mathematics)
In mathematics, a matrix (: matrices) is a rectangle, rectangular array or table of numbers, symbol (formal), symbols, or expression (mathematics), expressions, with elements or entries arranged in rows and columns, which is used to represent a mathematical object or property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two-by-three matrix", a " matrix", or a matrix of dimension . Matrices are commonly used in linear algebra, where they represent linear maps. In geometry, matrices are widely used for specifying and representing geometric transformations (for example rotation (mathematics), rotations) and coordinate changes. In numerical analysis, many computational problems are solved by reducing them to a matrix computation, and this often involves computing with matrices of huge dimensions. Matrices are used in most areas of mathematics and scientific fields, either directly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beta Decay Transition
In nuclear physics, a beta decay transition is the change in state of an atomic nucleus undergoing beta decay. When undergoing beta decay, a nucleus emits a beta particle and a corresponding neutrino, transforming the original nuclide into one with the same mass number but differing atomic number (nuclear charge). There are several types of beta decay transition. In a ''Fermi transition'', the spins of the two emitted particles are anti-parallel, for a combined spin S=0. As a result, the total angular momentum of the nucleus is unchanged by the transition. By contrast, in a ''Gamow-Teller'' transition, the spins of the two emitted particles are parallel, with total spin S=1, leading to a change in angular momentum between the initial and final states of the nucleus. The theoretical work in describing these transitions was done between 1934 and 1936 by George Gamow and Edward Teller at George Washington University. Weak interaction and beta decay Beta decay had been first ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermi's Golden Rule
In quantum physics, Fermi's golden rule is a formula that describes the transition rate (the probability of a transition per unit time) from one energy eigenstate of a quantum system to a group of energy eigenstates in a continuum, as a result of a weak Perturbation theory (quantum mechanics), perturbation. This transition rate is effectively independent of time (so long as the strength of the perturbation is independent of time) and is proportional to the strength of the coupling between the initial and final states of the system (described by the square of the Matrix element (physics), matrix element of the perturbation) as well as the density of states. It is also applicable when the final state is discrete, i.e. it is not part of a continuum, if there is some decoherence in the process, like relaxation or collision of the atoms, or like noise in the perturbation, in which case the density of states is replaced by the reciprocal of the decoherence bandwidth. Historical background ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helium
Helium (from ) is a chemical element; it has chemical symbol, symbol He and atomic number 2. It is a colorless, odorless, non-toxic, inert gas, inert, monatomic gas and the first in the noble gas group in the periodic table. Its boiling point is the lowest among all the Chemical element, elements, and it does not have a melting point at standard pressures. It is the second-lightest and second-most Abundance of the chemical elements, abundant element in the observable universe, after hydrogen. It is present at about 24% of the total elemental mass, which is more than 12 times the mass of all the heavier elements combined. Its abundance is similar to this in both the Sun and Jupiter, because of the very high nuclear binding energy (per nucleon) of helium-4 with respect to the next three elements after helium. This helium-4 binding energy also accounts for why it is a product of both nuclear fusion and radioactive decay. The most common isotope of helium in the universe is helium-4, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
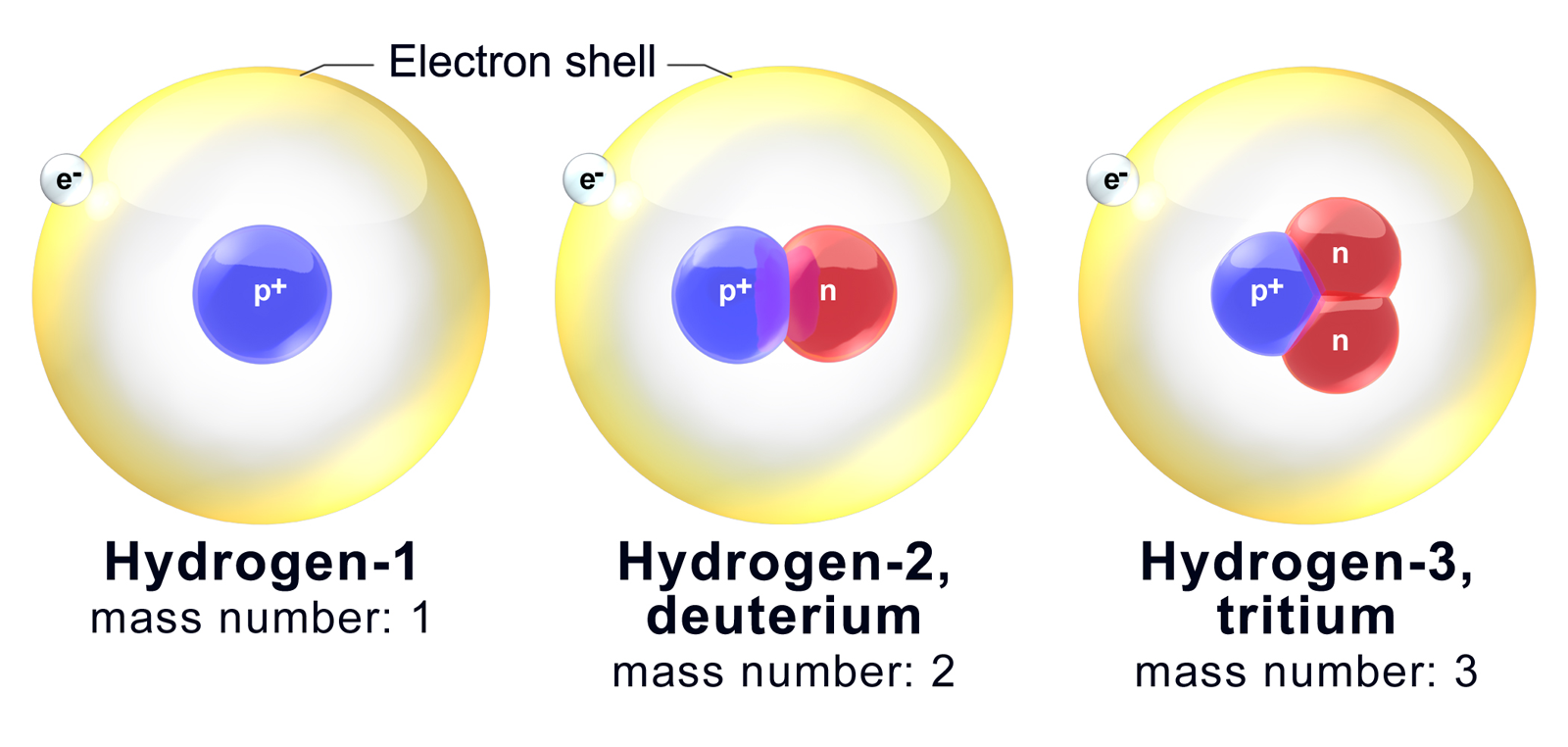
Hydrogen
Hydrogen is a chemical element; it has chemical symbol, symbol H and atomic number 1. It is the lightest and abundance of the chemical elements, most abundant chemical element in the universe, constituting about 75% of all baryon, normal matter. Under standard conditions, hydrogen is a gas of diatomic molecules with the chemical formula, formula , called dihydrogen, or sometimes hydrogen gas, molecular hydrogen, or simply hydrogen. Dihydrogen is colorless, odorless, non-toxic, and highly combustible. Stars, including the Sun, mainly consist of hydrogen in a plasma state, while on Earth, hydrogen is found as the gas (dihydrogen) and in molecular forms, such as in water and organic compounds. The most common isotope of hydrogen (H) consists of one proton, one electron, and no neutrons. Hydrogen gas was first produced artificially in the 17th century by the reaction of acids with metals. Henry Cavendish, in 1766–1781, identified hydrogen gas as a distinct substance and discovere ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum State
In quantum physics, a quantum state is a mathematical entity that embodies the knowledge of a quantum system. Quantum mechanics specifies the construction, evolution, and measurement of a quantum state. The result is a prediction for the system represented by the state. Knowledge of the quantum state, and the rules for the system's evolution in time, exhausts all that can be known about a quantum system. Quantum states may be defined differently for different kinds of systems or problems. Two broad categories are * wave functions describing quantum systems using position or momentum variables and * the more abstract vector quantum states. Historical, educational, and application-focused problems typically feature wave functions; modern professional physics uses the abstract vector states. In both categories, quantum states divide into pure versus mixed states, or into coherent states and incoherent states. Categories with special properties include stationary states for tim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthonormality
In linear algebra, two vector space, vectors in an inner product space are orthonormal if they are orthogonality, orthogonal unit vectors. A unit vector means that the vector has a length of 1, which is also known as normalized. Orthogonal means that the vectors are all perpendicular to each other. A set of vectors form an orthonormal set if all vectors in the set are mutually orthogonal and all of unit length. An orthonormal set which forms a basis (linear algebra), basis is called an ''orthonormal basis''. Intuitive overview The construction of orthogonality of vectors is motivated by a desire to extend the intuitive notion of perpendicular vectors to higher-dimensional spaces. In the Cartesian coordinate system#Cartesian coordinates in two dimensions, Cartesian plane, two Vector (geometry), vectors are said to be ''perpendicular'' if the angle between them is 90° (i.e. if they form a right angle). This definition can be formalized in Cartesian space by defining the dot produc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schrödinger Equation
The Schrödinger equation is a partial differential equation that governs the wave function of a non-relativistic quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. It is named after Erwin Schrödinger, an Austrian physicist, who postulated the equation in 1925 and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933. Conceptually, the Schrödinger equation is the quantum counterpart of Newton's second law in classical mechanics. Given a set of known initial conditions, Newton's second law makes a mathematical prediction as to what path a given physical system will take over time. The Schrödinger equation gives the evolution over time of the wave function, the quantum-mechanical characterization of an isolated physical system. The equation was postulated by Schrödinger based on a postulate of Louis de Broglie that all matter has an associated matter wave. The equati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Double Beta Decay
In nuclear physics, double beta decay is a type of radioactive decay in which two neutrons are simultaneously transformed into two protons, or vice versa, inside an atomic nucleus. As in single beta decay, this process allows the atom to move closer to the optimal ratio of protons and neutrons. As a result of this transformation, the nucleus emits two detectable beta particles, which are electrons or positrons. The literature distinguishes between two types of double beta decay: ''ordinary'' double beta decay and ''neutrinoless'' double beta decay. In ordinary double beta decay, which has been observed in several isotopes, two electrons and two electron antineutrinos are emitted from the decaying nucleus. In neutrinoless double beta decay, a hypothesized process that has never been observed, only electrons would be emitted. History The idea of double beta decay was first proposed by Maria Goeppert Mayer in 1935. In 1937, Ettore Majorana demonstrated that all results of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neutrinoless Double Beta Decay
Neutrinoless double beta decay (0νββ) is a commonly proposed and experimentally pursued theoretical radioactive decay process that would prove a Majorana particle, Majorana nature of the neutrino particle. To this day, it has not been found. The discovery of neutrinoless double beta decay could shed light on the absolute neutrino masses and on their mass hierarchy (Neutrino mass). It would mean the first ever signal of the violation of total lepton number conservation. A Majorana nature of neutrinos would confirm that the neutrino is its own antiparticle. To search for neutrinoless double beta decay, there are currently a number of experiments underway, with several future experiments for increased sensitivity proposed as well. History The Italian physicist Ettore Majorana first introduced the concept of a particle being its own antiparticle in 1937. Particles of this nature were subsequently named after him as Majorana particles. In 1939, Wendell H. Furry proposed the i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Particle Physics
Particle physics or high-energy physics is the study of Elementary particle, fundamental particles and fundamental interaction, forces that constitute matter and radiation. The field also studies combinations of elementary particles up to the scale of protons and neutrons, while the study of combinations of protons and neutrons is called nuclear physics. The fundamental particles in the universe are classified in the Standard Model as fermions (matter particles) and bosons (force-carrying particles). There are three Generation (particle physics), generations of fermions, although ordinary matter is made only from the first fermion generation. The first generation consists of Up quark, up and down quarks which form protons and neutrons, and electrons and electron neutrinos. The three fundamental interactions known to be mediated by bosons are electromagnetism, the weak interaction, and the strong interaction. Quark, Quarks cannot exist on their own but form hadrons. Hadrons that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Coefficient
In mathematics, a matrix coefficient (or matrix element) is a function on a group of a special form, which depends on a linear representation of the group and additional data. Precisely, it is a function on a compact topological group ''G'' obtained by composing a representation of ''G'' on a vector space ''V'' with a linear map from the endomorphisms of ''V'' into ''V'' underlying field. It is also called a representative function. They arise naturally from finite-dimensional representations of ''G'' as the matrix-entry functions of the corresponding matrix representations. The Peter–Weyl theorem says that the matrix coefficients on ''G'' are dense in the Hilbert space of square-integrable functions on ''G''. Matrix coefficients of representations of Lie groups turned out to be intimately related with the theory of special functions, providing a unifying approach to large parts of this theory. Growth properties of matrix coefficients play a key role in the classification ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |