|
Martingale Measure
In mathematical finance, a risk-neutral measure (also called an equilibrium measure, or ''equivalent martingale measure'') is a probability measure such that each share price is exactly equal to the discounted expectation of the share price under this measure. This is heavily used in the pricing of financial derivatives due to the fundamental theorem of asset pricing, which implies that in a complete market, a derivative's price is the discounted expected value of the future payoff under the unique risk-neutral measure. Such a measure exists if and only if the market is arbitrage-free. The easiest way to remember what the risk-neutral measure is, or to explain it to a probability generalist who might not know much about finance, is to realize that it is: # The probability measure of a transformed random variable. Typically this transformation is the utility function of the payoff. The risk-neutral measure would be the measure corresponding to an expectation of the payoff with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Finance
Mathematical finance, also known as quantitative finance and financial mathematics, is a field of applied mathematics, concerned with mathematical modeling of financial markets. In general, there exist two separate branches of finance that require advanced quantitative techniques: derivatives pricing on the one hand, and risk and portfolio management on the other. Mathematical finance overlaps heavily with the fields of computational finance and financial engineering. The latter focuses on applications and modeling, often by help of stochastic asset models, while the former focuses, in addition to analysis, on building tools of implementation for the models. Also related is quantitative investing, which relies on statistical and numerical models (and lately machine learning) as opposed to traditional fundamental analysis when managing portfolios. French mathematician Louis Bachelier's doctoral thesis, defended in 1900, is considered the first scholarly work on mathematical fina ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
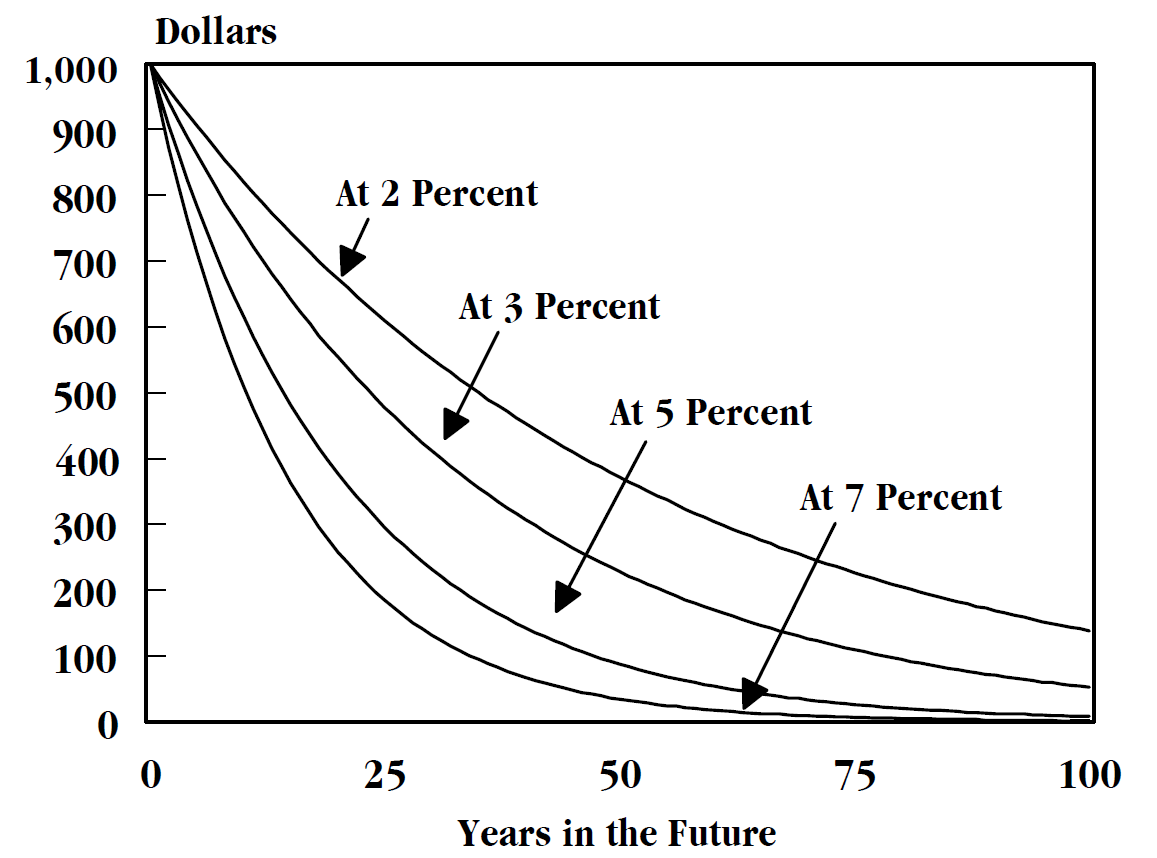
Risk-free Rate
The risk-free rate of return, usually shortened to the risk-free rate, is the rate of return of a hypothetical investment with scheduled payments over a fixed period of time that is assumed to meet all payment obligations. Since the risk-free rate can be obtained with no risk, any other investment having some risk will have to have a higher rate of return in order to induce any investors to hold it. In practice, to infer the risk-free interest rate in a particular currency, market participants often choose the yield to maturity on a risk-free bond issued by a government of the same currency whose risks of default are so low as to be negligible. For example, the rate of return on T-bills is sometimes seen as the risk-free rate of return in US dollars. Theoretical measurement As stated by Malcolm Kemp in chapter five of his book ''Market Consistency: Model Calibration in Imperfect Markets'', the risk-free rate means different things to different people and there is no consensus on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numéraire
The numéraire (or numeraire) is a basic standard by which value is computed. In mathematical economics it is a tradable economic entity in terms of whose price the relative prices of all other tradables are expressed. In a monetary economy, acting as the numéraire is one of the functions of money, to serve as a unit of account: to provide a common benchmark relative to which the worths of various goods and services are measured. This concept was confused between the properties of ‘money’ and ‘units of account’ until 1874-7, Leon Walras clarified it. He showed that the price can be expressed without introducing "money." Price can be translated in term of another. Using a numeraire, whether monetary or some consumable good, facilitates value comparisons when only the relative prices are relevant, as in general equilibrium theory. When economic analysis refers to a particular good as the numéraire, one says that all other prices are normalized by the price of that good. For ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Theorem Of Arbitrage-free Pricing
The fundamental theorems of asset pricing (also: of arbitrage, of finance), in both financial economics and mathematical finance, provide necessary and sufficient conditions for a market to be arbitrage-free, and for a market to be complete. An arbitrage opportunity is a way of making money with no initial investment without any possibility of loss. Though arbitrage opportunities do exist briefly in real life, it has been said that any sensible market model must avoid this type of profit.Pascucci, Andrea (2011) ''PDE and Martingale Methods in Option Pricing''. Berlin: Springer-Verlag The first theorem is important in that it ensures a fundamental property of market models. Completeness is a common property of market models (for instance the Black–Scholes model). A complete market is one in which every contingent claim can be replicated. Though this property is common in models, it is not always considered desirable or realistic. Discrete markets In a discrete (i.e. finite state) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discount Factor
Discounting is a financial mechanism in which a debtor obtains the right to delay payments to a creditor, for a defined period of time, in exchange for a charge or fee.See "Time Value", "Discount", "Discount Yield", "Compound Interest", "Efficient Market", "Market Value" and "Opportunity Cost" in Downes, J. and Goodman, J. E. ''Dictionary of Finance and Investment Terms'', Baron's Financial Guides, 2003. Essentially, the party that owes money in the present purchases the right to delay the payment until some future date.See "Discount", "Compound Interest", "Efficient Markets Hypothesis", "Efficient Resource Allocation", "Pareto-Optimality", "Price", "Price Mechanism" and "Efficient Market" in Black, John, ''Oxford Dictionary of Economics'', Oxford University Press, 2002. This transaction is based on the fact that most people prefer current interest to delayed interest because of mortality effects, impatience effects, and salience effects. The discount, or charge, is the difference ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Space
In probability theory, a probability space or a probability triple (\Omega, \mathcal, P) is a mathematical construct that provides a formal model of a random process or "experiment". For example, one can define a probability space which models the throwing of a die. A probability space consists of three elements:Stroock, D. W. (1999). Probability theory: an analytic view. Cambridge University Press. # A sample space, \Omega, which is the set of all possible outcomes. # An event space, which is a set of events \mathcal, an event being a set of outcomes in the sample space. # A probability function, which assigns each event in the event space a probability, which is a number between 0 and 1. In order to provide a sensible model of probability, these elements must satisfy a number of axioms, detailed in this article. In the example of the throw of a standard die, we would take the sample space to be \. For the event space, we could simply use the set of all subsets of the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a mathematical formalization of a quantity or object which depends on random events. It is a mapping or a function from possible outcomes (e.g., the possible upper sides of a flipped coin such as heads H and tails T) in a sample space (e.g., the set \) to a measurable space, often the real numbers (e.g., \ in which 1 corresponding to H and -1 corresponding to T). Informally, randomness typically represents some fundamental element of chance, such as in the roll of a dice; it may also represent uncertainty, such as measurement error. However, the interpretation of probability is philosophically complicated, and even in specific cases is not always straightforward. The purely mathematical analysis of random variables is independent of such interpretational difficulties, and can be based upon a rigorous axiomatic setup. In the formal mathematical language of measure theory, a random var ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stock
In finance, stock (also capital stock) consists of all the shares by which ownership of a corporation or company is divided.Longman Business English Dictionary: "stock - ''especially AmE'' one of the shares into which ownership of a company is divided, or these shares considered together" "When a company issues shares or stocks ''especially AmE'', it makes them available for people to buy for the first time." (Especially in American English, the word "stocks" is also used to refer to shares.) A single share of the stock means fractional ownership of the corporation in proportion to the total number of shares. This typically entitles the shareholder (stockholder) to that fraction of the company's earnings, proceeds from liquidation of assets (after discharge of all senior claims such as secured and unsecured debt), or voting power, often dividing these up in proportion to the amount of money each stockholder has invested. Not all stock is necessarily equal, as certain classe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Call Option
In finance, a call option, often simply labeled a "call", is a contract between the buyer and the seller of the call option to exchange a security at a set price. The buyer of the call option has the right, but not the obligation, to buy an agreed quantity of a particular commodity or financial instrument (the underlying) from the seller of the option at a certain time (the expiration date) for a certain price (the strike price). This effectively gives the owner a ''long'' position in the given asset. The seller (or "writer") is obliged to sell the commodity or financial instrument to the buyer if the buyer so decides. This effectively gives the seller a ''short'' position in the given asset. The buyer pays a fee (called a premium) for this right. The term "call" comes from the fact that the owner has the right to "call the stock away" from the seller. Price of options Option values vary with the value of the underlying instrument over time. The price of the call contract ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Double Digital Option
A double digital option is a particular variety of option (a financial derivative). At maturity, the payoff is 1 if the spot price of the underlying asset is between two numbers, the lower and upper strikes of the option; otherwise, it is 0. A double digital option is similar to the exotic option with a few exceptions. for instance a double digital option has two strike prices that is the expected price during the trade season. The option has two types of strikes namely the lower and the upper strikes. A double digital with lower strike ''K1'' and upper strike ''K2'' can be replicated by going long a digital option A binary option is a finance, financial exotic option in which the payoff is either some fixed monetary amount or nothing at all.Breeden, D. T., & Litzenberger, R. H. (1978). "Prices of state-contingent claims implicit in option prices". ''Journal ... with strike ''K1'' and short another digital option with strike ''K2''. References Options (finance) {{fin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Black–Scholes Model
The Black–Scholes or Black–Scholes–Merton model is a mathematical model for the dynamics of a financial market containing derivative investment instruments. From the parabolic partial differential equation in the model, known as the Black–Scholes equation, one can deduce the Black–Scholes formula, which gives a theoretical estimate of the price of European-style options and shows that the option has a ''unique'' price given the risk of the security and its expected return (instead replacing the security's expected return with the risk-neutral rate). The equation and model are named after economists Fischer Black and Myron Scholes; Robert C. Merton, who first wrote an academic paper on the subject, is sometimes also credited. The main principle behind the model is to hedge the option by buying and selling the underlying asset in a specific way to eliminate risk. This type of hedging is called "continuously revised delta hedging" and is the basis of more complicated ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |