|
Lattice Model (physics)
In mathematical physics, a lattice model is a mathematical model of a physical system that is defined on a lattice, as opposed to a continuum, such as the continuum of space or spacetime. Lattice models originally occurred in the context of condensed matter physics, where the atoms of a crystal automatically form a lattice. Currently, lattice models are quite popular in theoretical physics, for many reasons. Some models are exactly solvable, and thus offer insight into physics beyond what can be learned from perturbation theory. Lattice models are also ideal for study by the methods of computational physics, as the discretization of any continuum model automatically turns it into a lattice model. The exact solution to many of these models (when they are solvable) includes the presence of solitons. Techniques for solving these include the inverse scattering transform and the method of Lax pairs, the Yang–Baxter equation and quantum groups. The solution of these models has given i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Yang–Baxter Equation
In physics, the Yang–Baxter equation (or star–triangle relation) is a consistency equation which was first introduced in the field of statistical mechanics. It depends on the idea that in some scattering situations, particles may preserve their momentum while changing their quantum internal states. It states that a matrix R, acting on two out of three objects, satisfies :(\check\otimes \mathbf)(\mathbf\otimes \check)(\check\otimes \mathbf) =(\mathbf\otimes \check)(\check \otimes \mathbf)(\mathbf\otimes \check) In one dimensional quantum systems, R is the scattering matrix and if it satisfies the Yang–Baxter equation then the system is integrable. The Yang–Baxter equation also shows up when discussing knot theory and the braid groups where R corresponds to swapping two strands. Since one can swap three strands two different ways, the Yang–Baxter equation enforces that both paths are the same. It takes its name from independent work of C. N. Yang from 1968, and R. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice Gauge Theory
In physics, lattice gauge theory is the study of gauge theories on a spacetime that has been discretized into a lattice. Gauge theories are important in particle physics, and include the prevailing theories of elementary particles: quantum electrodynamics, quantum chromodynamics (QCD) and particle physics' Standard Model. Non-perturbative gauge theory calculations in continuous spacetime formally involve evaluating an infinite-dimensional path integral, which is computationally intractable. By working on a discrete spacetime, the path integral becomes finite-dimensional, and can be evaluated by stochastic simulation techniques such as the Monte Carlo method. When the size of the lattice is taken infinitely large and its sites infinitesimally close to each other, the continuum gauge theory is recovered. Basics In lattice gauge theory, the spacetime is Wick rotated into Euclidean space and discretized into a lattice with sites separated by distance a and connected by links. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Holographic Principle
The holographic principle is an axiom in string theories and a supposed property of quantum gravity that states that the description of a volume of space can be thought of as encoded on a lower-dimensional boundary to the region — such as a light-like boundary like a gravitational horizon. First proposed by Gerard 't Hooft, it was given a precise string-theory interpretation by Leonard Susskind, who combined his ideas with previous ones of 't Hooft and Charles Thorn. Leonard Susskind said, “The three-dimensional world of ordinary experience––the universe filled with galaxies, stars, planets, houses, boulders, and people––is a hologram, an image of reality coded on a distant two-dimensional surface." As pointed out by Raphael Bousso, Thorn observed in 1978 that string theory admits a lower-dimensional description in which gravity emerges from it in what would now be called a holographic way. The prime example of holography is the AdS/CFT correspondence. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
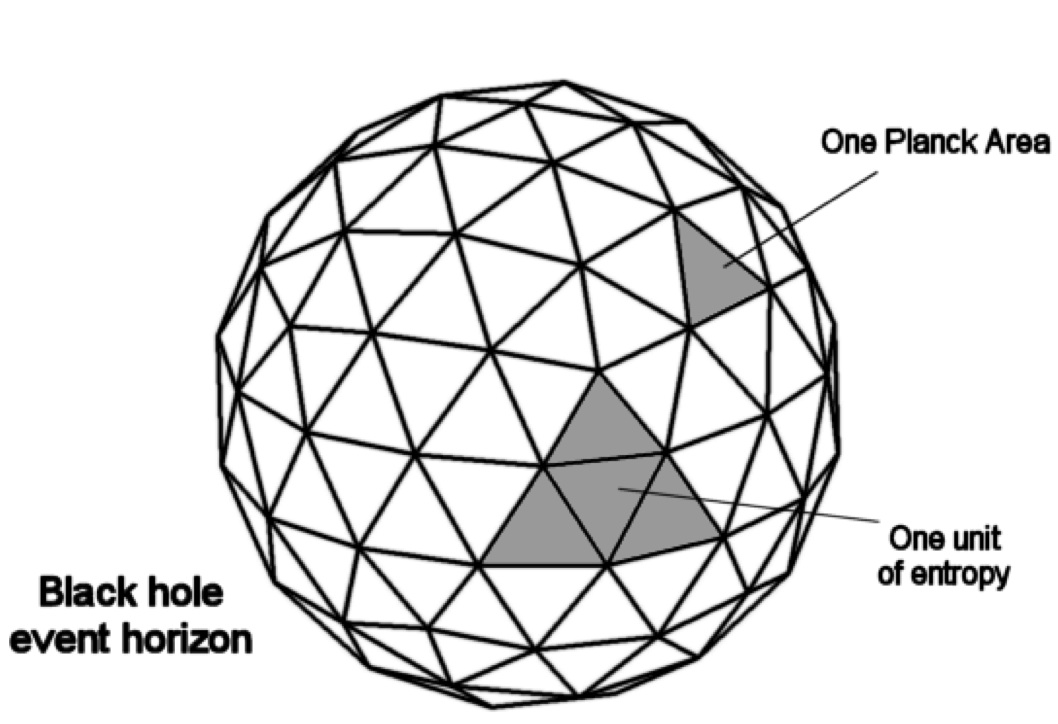
Bekenstein Bound
In physics, the Bekenstein bound (named after Jacob Bekenstein) is an upper limit on the thermodynamic entropy ''S'', or Shannon entropy ''H'', that can be contained within a given finite region of space which has a finite amount of energy—or conversely, the maximal amount of information required to perfectly describe a given physical system down to the quantum level. It implies that the information of a physical system, or the information necessary to perfectly describe that system, must be finite if the region of space and the energy are finite. In computer science this implies that non-finite models such as Turing machines are not realizable as finite devices. Equations The universal form of the bound was originally found by Jacob Bekenstein in 1981 as the inequality : S \leq \frac, where ''S'' is the entropy, ''k'' is the Boltzmann constant, ''R'' is the radius of a sphere that can enclose the given system, ''E'' is the total mass–energy including any rest masses, ''ħ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Digital Physics
Digital physics is a speculative idea that the universe can be conceived of as a vast, digital computation device, or as the output of a deterministic or probabilistic computer program. The hypothesis that the universe is a digital computer was proposed by Konrad Zuse in his 1969 book ''Rechnender Raum'' ("''Calculating Space''"). The term ''digital physics'' was coined by Edward Fredkin in 1978, who later came to prefer the term digital philosophy. Fredkin encouraged the creation of a digital physics group at what was then MIT's Laboratory for Computer Science, with Tommaso Toffoli and Norman Margolus as primary figures. ''Digital physics'' suggests that there exists, at least in principle, a program for a universal computer that computes the evolution of the universe. The computer could be, for example, a huge cellular automaton. Extant models of digital physics are incompatible with the existence of several continuous characters of physical symmetries, e.g., rotational symm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Chromodynamics
In theoretical physics, quantum chromodynamics (QCD) is the theory of the strong interaction between quarks mediated by gluons. Quarks are fundamental particles that make up composite hadrons such as the proton, neutron and pion. QCD is a type of quantum field theory called a non-abelian gauge theory, with symmetry group SU(3). The QCD analog of electric charge is a property called ''color''. Gluons are the force carriers of the theory, just as photons are for the electromagnetic force in quantum electrodynamics. The theory is an important part of the Standard Model of particle physics. A large body of experimental evidence for QCD has been gathered over the years. QCD exhibits three salient properties: * Color confinement. Due to the force between two color charges remaining constant as they are separated, the energy grows until a quark–antiquark pair is spontaneously produced, turning the initial hadron into a pair of hadrons instead of isolating a color charge. Although ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
QCD Lattice Model
Lattice QCD is a well-established non-perturbative approach to solving the quantum chromodynamics (QCD) theory of quark A quark () is a type of elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. All commonly o ...s and gluons. It is a lattice gauge theory formulated on a grid or lattice (group), lattice of points in space and time. When the size of the lattice is taken infinitely large and its sites infinitesimally close to each other, the continuum QCD is recovered. Analytic or perturbative solutions in low-energy QCD are hard or impossible to obtain due to the highly nonlinear nature of the strong force and the large Coupling constant#QCD and asymptotic freedom, coupling constant at low energies. This formulation of QCD in discrete rather than continuous spacetime naturally introduces a momentum cut-off at the order 1/''a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic computation, symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods that attempt at finding approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics (predicting the motions of planets, stars and galaxies), numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living ce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ultraviolet Cutoff
In theoretical physics, cutoff (AE: cutoff, BE: cut-off) is an arbitrary maximal or minimal value of energy, momentum, or length, used in order that objects with larger or smaller values than these physical quantities are ignored in some calculation. It is usually represented within a particular energy or length scale, such as Planck units. When used in this context, the traditional terms "infrared" and "ultraviolet" are not literal references to specific regions of the spectrum, but rather refer by analogy to portions of a calculation for low energies (infrared) and high energies (ultraviolet), respectively. Infrared and ultraviolet cutoff An infrared cutoff (long-distance cutoff) is the minimal value of energy – or, equivalently, the maximal wavelength (usually a very large distance) – that will be taken into account in a calculation, typically an integral. At the opposite end of the energy scale, an ultraviolet cutoff is the maximal allowed energy or the shortest allowed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Field Theory
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines classical field theory, special relativity, and quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles and in condensed matter physics to construct models of quasiparticles. QFT treats particles as excited states (also called Quantum, quanta) of their underlying quantum field (physics), fields, which are more fundamental than the particles. The equation of motion of the particle is determined by minimization of the Lagrangian, a functional of fields associated with the particle. Interactions between particles are described by interaction terms in the Lagrangian (field theory), Lagrangian involving their corresponding quantum fields. Each interaction can be visually represented by Feynman diagrams according to perturbation theory (quantum mechanics), perturbation theory in quantum mechanics. History Quantum field theory emerged from the wo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scaling Behaviour
Scaling may refer to: Science and technology Mathematics and physics * Scaling (geometry), a linear transformation that enlarges or diminishes objects * Scale invariance, a feature of objects or laws that do not change if scales of length, energy, or other variables are multiplied by a common factor ** Scaling law, a law that describes the scale invariance found in many natural phenomena * The scaling of critical exponents in physics, such as Widom scaling, or scaling of the renormalization group Computing and information technology * Feature scaling, a method used to standardize the range of independent variables or features of data * Image scaling, the resizing of an image * Multidimensional scaling, a means of visualizing the level of similarity of individual cases of a dataset * Scalability, a computer's or network's ability to function as the number of users increases * Scaling along the Z axis, a technique used in computer graphics for a pseudo-3D effect * Reduced scales o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |