|
Loopy Game
In combinatorial game theory, a branch of mathematics, a loopy game is one in which a previous state is reachable from descendent options. By contrast, a loop-free game is a game where players can never reach previous positions. A loop-free finite game is also called a ''short'' game. Some loopy games with combinatorial game theory notation include: * dud: ("deathless universal draw") * on: * off: Some interesting properties arise from these definitions. For example, on + off = dud, or dud + G = dud for any game G. Like transfinite games, the infinite nature of loopy games gives an extra outcome to loopy games: a tie. A player 'survives' a game if they either tie or win. Impartial loopy games are susceptible to analysis by the generalized Sprague-Grundy theorem. Definition A loopy game is a pair G = (V, x), where V is a bipartite graph with named edge-sets (that is, some edges of the bipartite graph are Left, and other edges are Right) and x is the ''start vertex'' ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Combinatorial Game Theory
Combinatorial game theory is a branch of mathematics and theoretical computer science that typically studies sequential games with perfect information. Study has been largely confined to two-player games that have a ''position'' that the players take turns changing in defined ways or ''moves'' to achieve a defined winning condition. Combinatorial game theory has not traditionally studied games of chance or those that use imperfect or incomplete information, favoring games that offer perfect information in which the state of the game and the set of available moves is always known by both players. However, as mathematical techniques advance, the types of game that can be mathematically analyzed expands, thus the boundaries of the field are ever changing. Scholars will generally define what they mean by a "game" at the beginning of a paper, and these definitions often vary as they are specific to the game being analyzed and are not meant to represent the entire scope of the field. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bipartite Graph
In the mathematical field of graph theory, a bipartite graph (or bigraph) is a graph whose vertices can be divided into two disjoint and independent sets U and V, that is every edge connects a vertex in U to one in V. Vertex sets U and V are usually called the ''parts'' of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles. The two sets U and V may be thought of as a coloring of the graph with two colors: if one colors all nodes in U blue, and all nodes in V red, each edge has endpoints of differing colors, as is required in the graph coloring problem.. In contrast, such a coloring is impossible in the case of a non-bipartite graph, such as a triangle: after one node is colored blue and another red, the third vertex of the triangle is connected to vertices of both colors, preventing it from being assigned either color. One often writes G=(U,V,E) to denote a bipartite graph whose partition has the parts U and V, with E denotin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
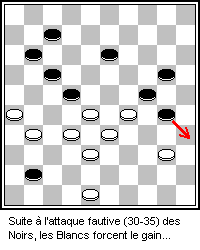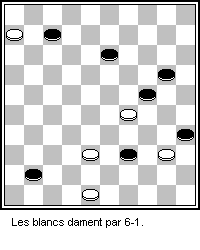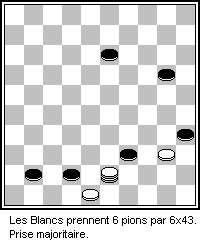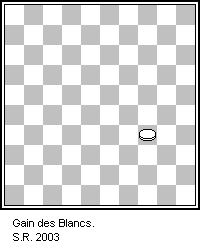
Checkers
Checkers (American English), also known as draughts (; British English), is a group of strategy board games for two players which involve diagonal moves of uniform game pieces and mandatory captures by jumping over opponent pieces. Checkers is developed from alquerque. The term "checkers" derives from the checkered board which the game is played on, whereas "draughts" derives from the verb "to draw" or "to move". The most popular forms of checkers in Anglophone countries are American checkers (also called English draughts), which is played on an 8×8 checkerboard; Russian draughts, Turkish draughts both on an 8x8 board, and International draughts, played on a 10×10 board – the latter is widely played in many countries worldwide. There are many other variants played on 8×8 boards. Canadian checkers and Singaporean/Malaysian checkers (also locally known as ''dum'') are played on a 12×12 board. American checkers was weakly solved in 2007 by a team of Canadian compu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fox And Geese
Fox games are a category of asymmetric board games for two players, where one player is the fox and tries to eat the geese / sheep, and the opposing player directs the geese/sheep and attempts to trap the fox, or reach a destination on the board. In another variant, ''Fox and Hounds'', the fox merely tries to evade the hounds. There are several versions known: History The game ''Halatafl'' is known from at least as early as the 14th century, and it is mentioned in Grettis saga. It probably originated in Scandinavia, as a variant of Tafl. In fact, Halatafl is still played in Scandinavia with rules similar to Tafl; see below. Edward IV of England is known to have purchased two foxes and 26 hounds to form two sets of ''Marelles'', believed to be Fox and Hounds. As Fox and Geese, the game was a favorite pastime of Queen Victoria. Halatafl ''Halatafl'' means "tail board", in Old Norse, and "tail" presumably refers to a fox's tail. As in Grettis saga, ''rävspelet'' (modern Swe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |