|
Kōnane
Kōnane is a two-player strategy board game from Hawaii. It was invented by the ancient Hawaiian Polynesians. The game is played on a rectangular board. It begins with black and white counters filling the board in an alternating pattern. Players then hop over one another's pieces, capturing them similar to checkers. The first player unable to capture is the loser; their opponent is the winner. Before contact with Europeans, the game was played using small pieces of white coral and black lava on a large carved rock which doubled as both board and table. The Puʻuhonua o Hōnaunau National Historical Park has one of these stone gameboards on its premises. The game is somewhat similar to draughts. Pieces hop over one another when capturing; however, the similarities end there. In draughts, one player's pieces are initially set up on one side of the board opposite the other player's pieces. In Kōnane, both players' pieces are intermixed in a checkered pattern of black and whit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Draughts
Checkers (American English), also known as draughts (; British English), is a group of strategy board games for two players which involve diagonal moves of uniform game pieces and mandatory captures by jumping over opponent pieces. Checkers is developed from alquerque. The term "checkers" derives from the checkered board which the game is played on, whereas "draughts" derives from the verb "to draw" or "to move". The most popular forms of checkers in Anglophone countries are American checkers (also called English draughts), which is played on an 8×8 checkerboard; Russian draughts, Turkish draughts both on an 8x8 board, and International draughts, played on a 10×10 board – the latter is widely played in many countries worldwide. There are many other variants played on 8×8 boards. Canadian checkers and Singaporean/Malaysian checkers (also locally known as ''dum'') are played on a 12×12 board. American checkers was weakly solved in 2007 by a team of Canadian compu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Combinatorial Game Theory
Combinatorial game theory is a branch of mathematics and theoretical computer science that typically studies sequential games with perfect information. Study has been largely confined to two-player games that have a ''position'' that the players take turns changing in defined ways or ''moves'' to achieve a defined winning condition. Combinatorial game theory has not traditionally studied games of chance or those that use imperfect or incomplete information, favoring games that offer perfect information in which the state of the game and the set of available moves is always known by both players. However, as mathematical techniques advance, the types of game that can be mathematically analyzed expands, thus the boundaries of the field are ever changing. Scholars will generally define what they mean by a "game" at the beginning of a paper, and these definitions often vary as they are specific to the game being analyzed and are not meant to represent the entire scope of the field. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematicians Playing Konane
A mathematician is someone who uses an extensive knowledge of mathematics in their work, typically to solve mathematical problems. Mathematicians are concerned with numbers, data, quantity, structure, space, models, and change. History One of the earliest known mathematicians were Thales of Miletus (c. 624–c.546 BC); he has been hailed as the first true mathematician and the first known individual to whom a mathematical discovery has been attributed. He is credited with the first use of deductive reasoning applied to geometry, by deriving four corollaries to Thales' Theorem. The number of known mathematicians grew when Pythagoras of Samos (c. 582–c. 507 BC) established the Pythagorean School, whose doctrine it was that mathematics ruled the universe and whose motto was "All is number". It was the Pythagoreans who coined the term "mathematics", and with whom the study of mathematics for its own sake begins. The first woman mathematician recorded by history was Hypat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abstract Strategy
Abstract strategy games admit a number of definitions which distinguish these from strategy games in general, mostly involving no or minimal narrative theme, outcomes determined only by player choice (with no randomness), and perfect information. For example, Go is a pure abstract strategy game since it fulfills all three criteria; chess and related games are nearly so but feature a recognizable theme of ancient warfare; and Stratego is borderline since it is deterministic, loosely based on 19th-century Napoleonic warfare, and features concealed information. Definition Combinatorial games have no randomizers such as dice, no simultaneous movement, nor hidden information. Some games that do have these elements are sometimes classified as abstract strategy games. (Games such as '' Continuo'', Octiles, '' Can't Stop'', and Sequence, could be considered abstract strategy games, despite having a luck or bluffing element.) A smaller category of abstract strategy games manages to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Board Game
Board games are tabletop games that typically use . These pieces are moved or placed on a pre-marked board (playing surface) and often include elements of table, card, role-playing, and miniatures games as well. Many board games feature a competition between two or more players. To show a few examples: in checkers (British English name 'draughts'), a player wins by capturing all opposing pieces, while Eurogames often end with a calculation of final scores. ''Pandemic'' is a cooperative game where players all win or lose as a team, and peg solitaire is a puzzle for one person. There are many varieties of board games. Their representation of real-life situations can range from having no inherent theme, such as checkers, to having a specific theme and narrative, such as '' Cluedo''. Rules can range from the very simple, such as in snakes and ladders; to deeply complex, as in '' Advanced Squad Leader''. Play components now often include custom figures or shaped counters, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hawaii
Hawaii ( ; haw, Hawaii or ) is a state in the Western United States, located in the Pacific Ocean about from the U.S. mainland. It is the only U.S. state outside North America, the only state that is an archipelago, and the only state geographically located within the tropics. Hawaii comprises nearly the entire Hawaiian archipelago, 137 volcanic islands spanning that are physiographically and ethnologically part of the Polynesian subregion of Oceania. The state's ocean coastline is consequently the fourth-longest in the U.S., at about . The eight main islands, from northwest to southeast, are Niihau, Kauai, Oahu, Molokai, Lānai, Kahoolawe, Maui, and Hawaii—the last of these, after which the state is named, is often called the "Big Island" or "Hawaii Island" to avoid confusion with the state or archipelago. The uninhabited Northwestern Hawaiian Islands make up most of the Papahānaumokuākea Marine National Monument, the United States' largest prot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Puʻuhonua O Hōnaunau National Historical Park
Puʻuhonua o Hōnaunau National Historical Park is a United States National Historical Park located on the west coast of the island of Hawaiʻi in the U.S. state of Hawaii. The historical park preserves the site where, up until the early 19th century, Hawaiians who broke a kapu (one of the ancient laws) could avoid certain death by fleeing to this place of refuge or ''puʻuhonua''. The offender would be absolved by a priest and freed to leave. Defeated warriors and non-combatants could also find refuge here during times of battle. The grounds just outside the Great Wall that encloses the puʻuhonua were home to several generations of powerful chiefs. Puʻuhonua o Hōnaunau is one of the only places in Hawaii where the flag of Hawaii can officially fly alone without the American flag; the other three places are ʻIolani Palace, the Mauna ʻAla and Thomas Square. Park name and features The 420 acre (1.7 km2) site was originally established in 1955 as City of Refuge Nation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonality
In mathematics, orthogonality is the generalization of the geometric notion of '' perpendicularity''. By extension, orthogonality is also used to refer to the separation of specific features of a system. The term also has specialized meanings in other fields including art and chemistry. Etymology The word comes from the Ancient Greek ('), meaning "upright", and ('), meaning "angle". The Ancient Greek (') and Classical Latin ' originally denoted a rectangle. Later, they came to mean a right triangle. In the 12th century, the post-classical Latin word ''orthogonalis'' came to mean a right angle or something related to a right angle. Mathematics Physics * In optics, polarization states are said to be orthogonal when they propagate independently of each other, as in vertical and horizontal linear polarization or right- and left-handed circular polarization. * In special relativity, a time axis determined by a rapidity of motion is hyperbolic-orthogonal to a space axis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leap Frog (board Game)
Leap Frog, also known as Leapfrog, is a multi-player abstract strategy board game that was described by H.J.R. Murray in ''A History of Board Games Other Than Chess'' (1898) and attributes its origin to England. Several variants have been created (see Variants section) including one by Murray himself which utilizes different colored pieces with different point values. Several players can participate. In the traditional game, players take any piece on the board and use it to hop over and capture other pieces on the board. When no more pieces can be captured, the game ends, and the player with the most pieces wins the game. Murray includes it in the section called Clearance Games which includes the game Solitaire which it does resemble in many ways except that Solitaire is played by only one person. Murray never stated that the moves are limited to orthogonal directions. The game might still work with diagonal moves. Setup A rectangular board with 15 to 18 squares in length ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
PSPACE-complete
In computational complexity theory, a decision problem is PSPACE-complete if it can be solved using an amount of memory that is polynomial in the input length ( polynomial space) and if every other problem that can be solved in polynomial space can be transformed to it in polynomial time. The problems that are PSPACE-complete can be thought of as the hardest problems in PSPACE, the class of decision problems solvable in polynomial space, because a solution to any one such problem could easily be used to solve any other problem in PSPACE. Problems known to be PSPACE-complete include determining properties of regular expressions and context-sensitive grammars, determining the truth of quantified Boolean formulas, step-by-step changes between solutions of combinatorial optimization problems, and many puzzles and games. Theory A problem is defined to be PSPACE-complete if it can be solved using a polynomial amount of memory (it belongs to PSPACE) and every problem in PSPACE can be t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

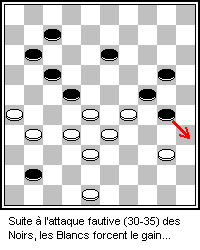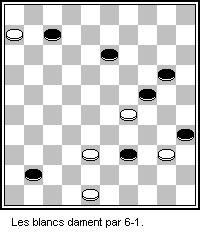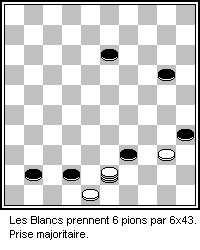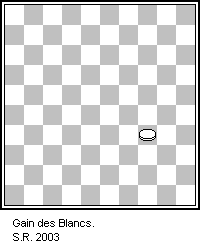

_--_2021_--_6741.jpg)


