|
Kernel Method
In machine learning, kernel machines are a class of algorithms for pattern analysis, whose best known member is the support-vector machine (SVM). The general task of pattern analysis is to find and study general types of relations (for example clusters, rankings, principal components, correlations, classifications) in datasets. For many algorithms that solve these tasks, the data in raw representation have to be explicitly transformed into feature vector representations via a user-specified ''feature map'': in contrast, kernel methods require only a user-specified ''kernel'', i.e., a similarity function over all pairs of data points computed using Inner products. The feature map in kernel machines is infinite dimensional but only requires a finite dimensional matrix from user-input according to the Representer theorem. Kernel machines are slow to compute for datasets larger than a couple of thousand examples without parallel processing. Kernel methods owe their name to th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Machine Learning
Machine learning (ML) is a field of inquiry devoted to understanding and building methods that 'learn', that is, methods that leverage data to improve performance on some set of tasks. It is seen as a part of artificial intelligence. Machine learning algorithms build a model based on sample data, known as training data, in order to make predictions or decisions without being explicitly programmed to do so. Machine learning algorithms are used in a wide variety of applications, such as in medicine, email filtering, speech recognition, agriculture, and computer vision, where it is difficult or unfeasible to develop conventional algorithms to perform the needed tasks.Hu, J.; Niu, H.; Carrasco, J.; Lennox, B.; Arvin, F.,Voronoi-Based Multi-Robot Autonomous Exploration in Unknown Environments via Deep Reinforcement Learning IEEE Transactions on Vehicular Technology, 2020. A subset of machine learning is closely related to computational statistics, which focuses on making pred ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kernel Perceptron
In machine learning, the kernel perceptron is a variant of the popular perceptron learning algorithm that can learn kernel machines, i.e. non-linear classifiers that employ a kernel function to compute the similarity of unseen samples to training samples. The algorithm was invented in 1964, making it the first kernel classification learner. Preliminaries The perceptron algorithm The perceptron algorithm is an online learning algorithm that operates by a principle called "error-driven learning". It iteratively improves a model by running it on training samples, then updating the model whenever it finds it has made an incorrect classification with respect to a supervised signal. The model learned by the standard perceptron algorithm is a linear binary classifier: a vector of weights (and optionally an intercept term , omitted here for simplicity) that is used to classify a sample vector as class "one" or class "minus one" according to :\hat = \sgn(\mathbf^\top \mathbf) where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sign Function
In mathematics, the sign function or signum function (from '' signum'', Latin for "sign") is an odd mathematical function that extracts the sign of a real number. In mathematical expressions the sign function is often represented as . To avoid confusion with the sine function, this function is usually called the signum function. Definition The signum function of a real number is a piecewise function which is defined as follows: \sgn x :=\begin -1 & \text x 0. \end Properties Any real number can be expressed as the product of its absolute value and its sign function: x = , x, \sgn x. It follows that whenever is not equal to 0 we have \sgn x = \frac = \frac\,. Similarly, for ''any'' real number , , x, = x\sgn x. We can also ascertain that: \sgn x^n=(\sgn x)^n. The signum function is the derivative of the absolute value function, up to (but not including) the indeterminacy at zero. More formally, in integration theory it is a weak derivative, and in convex fun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Classifier
Binary classification is the task of classifying the elements of a set into two groups (each called ''class'') on the basis of a classification rule. Typical binary classification problems include: * Medical testing to determine if a patient has certain disease or not; * Quality control in industry, deciding whether a specification has been met; * In information retrieval, deciding whether a page should be in the result set of a search or not. Binary classification is dichotomization applied to a practical situation. In many practical binary classification problems, the two groups are not symmetric, and rather than overall accuracy, the relative proportion of different types of errors is of interest. For example, in medical testing, detecting a disease when it is not present (a ''false positive'') is considered differently from not detecting a disease when it is present (a ''false negative''). Statistical binary classification Statistical classification is a problem studied i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Instance-based Learning
In machine learning, instance-based learning (sometimes called memory-based learning) is a family of learning algorithms that, instead of performing explicit generalization, compare new problem instances with instances seen in training, which have been stored in memory. Because computation is postponed until a new instance is observed, these algorithms are sometimes referred to as "lazy." It is called instance-based because it constructs hypotheses directly from the training instances themselves. Stuart Russell and Peter Norvig (2003). '' Artificial Intelligence: A Modern Approach'', second edition, p. 733. Prentice Hall. This means that the hypothesis complexity can grow with the data: in the worst case, a hypothesis is a list of ''n'' training items and the computational complexity of classifying a single new instance is ''O''(''n''). One advantage that instance-based learning has over other methods of machine learning is its ability to adapt its model to previously unseen data. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rademacher Complexity
In computational learning theory (machine learning and theory of computation), Rademacher complexity, named after Hans Rademacher, measures richness of a class of real-valued functions with respect to a probability distribution. Definitions Rademacher complexity of a set Given a set A\subseteq \mathbb^m, the Rademacher complexity of ''A'' is defined as follows:Chapter 26 in : \operatorname(A) := \frac \mathbb_\sigma \left \sup_ \sum_^m \sigma_i a_i \right where \sigma_1, \sigma_2, \dots, \sigma_m are independent random variables drawn from the Rademacher distribution i.e. \Pr(\sigma_i = +1) = \Pr(\sigma_i = -1) = 1/2 for i=1,2,\dots,m, and a=(a_1, \ldots, a_m). Some authors take the absolute value of the sum before taking the supremum, but if A is symmetric this makes no difference. Rademacher complexity of a function class Let S=(z_1, z_2, \dots, z_m) \in Z^m be a sample of points and consider a function class \mathcal of real-valued functions over Z^m. Then ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Learning Theory
Statistical learning theory is a framework for machine learning drawing from the fields of statistics and functional analysis. Statistical learning theory deals with the statistical inference problem of finding a predictive function based on data. Statistical learning theory has led to successful applications in fields such as computer vision, speech recognition, and bioinformatics. Introduction The goals of learning are understanding and prediction. Learning falls into many categories, including supervised learning, unsupervised learning, online learning, and reinforcement learning. From the perspective of statistical learning theory, supervised learning is best understood. Supervised learning involves learning from a training set of data. Every point in the training is an input-output pair, where the input maps to an output. The learning problem consists of inferring the function that maps between the input and the output, such that the learned function can be used to pre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalue, Eigenvector And Eigenspace
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by \lambda, is the factor by which the eigenvector is scaled. Geometrically, an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction in which it is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed. Loosely speaking, in a multidimensional vector space, the eigenvector is not rotated. Formal definition If is a linear transformation from a vector space over a field into itself and is a nonzero vector in , then is an eigenvector of if is a scalar multiple of . This can be written as T(\mathbf) = \lambda \mathbf, where is a scalar in , known as the eigenvalue, characteristic value, or characteristic root ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
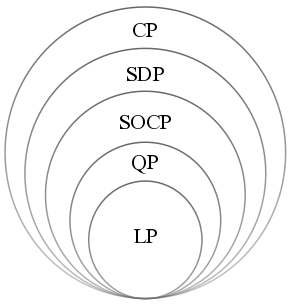
Convex Optimization
Convex optimization is a subfield of mathematical optimization that studies the problem of minimizing convex functions over convex sets (or, equivalently, maximizing concave functions over convex sets). Many classes of convex optimization problems admit polynomial-time algorithms, whereas mathematical optimization is in general NP-hard. Convex optimization has applications in a wide range of disciplines, such as automatic control systems, estimation and signal processing, communications and networks, electronic circuit design, data analysis and modeling, finance, statistics (optimal experimental design), and structural optimization, where the approximation concept has proven to be efficient. With recent advancements in computing and optimization algorithms, convex programming is nearly as straightforward as linear programming. Definition A convex optimization problem is an optimization problem in which the objective function is a convex function and the feasible set ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adaptive Filter
An adaptive filter is a system with a linear filter that has a transfer function controlled by variable parameters and a means to adjust those parameters according to an optimization algorithm. Because of the complexity of the optimization algorithms, almost all adaptive filters are digital filters. Adaptive filters are required for some applications because some parameters of the desired processing operation (for instance, the locations of reflective surfaces in a reverberant space) are not known in advance or are changing. The closed loop adaptive filter uses feedback in the form of an error signal to refine its transfer function. Generally speaking, the closed loop adaptive process involves the use of a cost function, which is a criterion for optimum performance of the filter, to feed an algorithm, which determines how to modify filter transfer function to minimize the cost on the next iteration. The most common cost function is the mean square of the error signal. As the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Clustering
In multivariate statistics, spectral clustering techniques make use of the spectrum (eigenvalues) of the similarity matrix of the data to perform dimensionality reduction before clustering in fewer dimensions. The similarity matrix is provided as an input and consists of a quantitative assessment of the relative similarity of each pair of points in the dataset. In application to image segmentation, spectral clustering is known as segmentation-based object categorization. Definitions Given an enumerated set of data points, the similarity matrix may be defined as a symmetric matrix A, where A_\geq 0 represents a measure of the similarity between data points with indices i and j. The general approach to spectral clustering is to use a standard clustering method (there are many such methods, ''k''-means is discussed below) on relevant eigenvectors of a Laplacian matrix of A. There are many different ways to define a Laplacian which have different mathematical interpretations, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ridge Regression
Ridge regression is a method of estimating the coefficients of multiple- regression models in scenarios where the independent variables are highly correlated. It has been used in many fields including econometrics, chemistry, and engineering. Also known as Tikhonov regularization, named for Andrey Tikhonov, it is a method of regularization of ill-posed problems. It is particularly useful to mitigate the problem of multicollinearity in linear regression, which commonly occurs in models with large numbers of parameters. In general, the method provides improved efficiency in parameter estimation problems in exchange for a tolerable amount of bias (see bias–variance tradeoff). The theory was first introduced by Hoerl and Kennard in 1970 in their '' Technometrics'' papers “RIDGE regressions: biased estimation of nonorthogonal problems” and “RIDGE regressions: applications in nonorthogonal problems”. This was the result of ten years of research into the field of ridge an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |