|
Joint Quantum Entropy
The joint quantum entropy generalizes the classical joint entropy to the context of quantum information theory. Intuitively, given two quantum states \rho and \sigma, represented as density operators that are subparts of a quantum system, the joint quantum entropy is a measure of the total uncertainty or entropy of the joint system. It is written S(\rho,\sigma) or H(\rho,\sigma), depending on the notation being used for the von Neumann entropy. Like other entropies, the joint quantum entropy is measured in bits, i.e. the logarithm is taken in base 2. In this article, we will use S(\rho,\sigma) for the joint quantum entropy. Background In information theory, for any classical random variable X, the classical Shannon entropy H(X) is a measure of how uncertain we are about the outcome of X. For example, if X is a probability distribution concentrated at one point, the outcome of X is certain and therefore its entropy H(X)=0. At the other extreme, if X is the uniform probabilit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Joint Entropy
In information theory, joint entropy is a measure of the uncertainty associated with a set of variables. Definition The joint Shannon entropy (in bits) of two discrete random variables X and Y with images \mathcal X and \mathcal Y is defined as where x and y are particular values of X and Y, respectively, P(x,y) is the joint probability of these values occurring together, and P(x,y) \log_2 (x,y)/math> is defined to be 0 if P(x,y)=0. For more than two random variables X_1, ..., X_n this expands to where x_1,...,x_n are particular values of X_1,...,X_n, respectively, P(x_1, ..., x_n) is the probability of these values occurring together, and P(x_1, ..., x_n) \log_2 (x_1, ..., x_n)/math> is defined to be 0 if P(x_1, ..., x_n)=0. Properties Nonnegativity The joint entropy of a set of random variables is a nonnegative number. :\Eta(X,Y) \geq 0 :\Eta(X_1,\ldots, X_n) \geq 0 Greater than individual entropies The joint entropy of a set of variables is greater than or eq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pure State
In quantum physics, a quantum state is a mathematical entity that provides a probability distribution for the outcomes of each possible measurement on a system. Knowledge of the quantum state together with the rules for the system's evolution in time exhausts all that can be predicted about the system's behavior. A mixture of quantum states is again a quantum state. Quantum states that cannot be written as a mixture of other states are called pure quantum states, while all other states are called mixed quantum states. A pure quantum state can be represented by a ray in a Hilbert space over the complex numbers, while mixed states are represented by density matrices, which are positive semidefinite operators that act on Hilbert spaces. Pure states are also known as state vectors or wave functions, the latter term applying particularly when they are represented as functions of position or momentum. For example, when dealing with the energy spectrum of the electron in a hydrogen ato ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mutual Information
In quantum information theory, quantum mutual information, or von Neumann mutual information, after John von Neumann, is a measure of correlation between subsystems of quantum state. It is the quantum mechanical analog of Shannon mutual information. Motivation For simplicity, it will be assumed that all objects in the article are finite-dimensional. The definition of quantum mutual entropy is motivated by the classical case. For a probability distribution of two variables ''p''(''x'', ''y''), the two marginal distributions are :p(x) = \sum_ p(x,y), \qquad p(y) = \sum_ p(x,y). The classical mutual information ''I''(''X'':''Y'') is defined by :I(X:Y) = S(p(x)) + S(p(y)) - S(p(x,y)) where ''S''(''q'') denotes the Shannon entropy of the probability distribution ''q''. One can calculate directly :\begin S(p(x)) + S(p(y)) &= - \left (\sum_x p_x \log p(x) + \sum_y p_y \log p(y) \right ) \\ &= -\left (\sum_x \left ( \sum_ p(x,y') \log \sum_ p(x,y') \right ) + \sum_y \left ( \s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Relative Entropy
In quantum information theory, quantum relative entropy is a measure of distinguishability between two density matrix, quantum states. It is the quantum mechanical analog of relative entropy. Motivation For simplicity, it will be assumed that all objects in the article are finite-dimensional. We first discuss the classical case. Suppose the probabilities of a finite sequence of events is given by the probability distribution ''P'' = , but somehow we mistakenly assumed it to be ''Q'' = . For instance, we can mistake an unfair coin for a fair one. According to this erroneous assumption, our uncertainty about the ''j''-th event, or equivalently, the amount of information provided after observing the ''j''-th event, is :\; - \log q_j. The (assumed) average uncertainty of all possible events is then :\; - \sum_j p_j \log q_j. On the other hand, the Shannon entropy of the probability distribution ''p'', defined by :\; - \sum_j p_j \log p_j, is the real amount of uncertainty befor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mutual Information
In probability theory and information theory, the mutual information (MI) of two random variables is a measure of the mutual dependence between the two variables. More specifically, it quantifies the " amount of information" (in units such as shannons (bits), nats or hartleys) obtained about one random variable by observing the other random variable. The concept of mutual information is intimately linked to that of entropy of a random variable, a fundamental notion in information theory that quantifies the expected "amount of information" held in a random variable. Not limited to real-valued random variables and linear dependence like the correlation coefficient, MI is more general and determines how different the joint distribution of the pair (X,Y) is from the product of the marginal distributions of X and Y. MI is the expected value of the pointwise mutual information (PMI). The quantity was defined and analyzed by Claude Shannon in his landmark paper "A Mathemati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Entropy
In information theory, the conditional entropy quantifies the amount of information needed to describe the outcome of a random variable Y given that the value of another random variable X is known. Here, information is measured in shannons, nats, or hartley Hartley may refer to: Places Australia *Hartley, New South Wales *Hartley, South Australia **Electoral district of Hartley, a state electoral district Canada *Hartley Bay, British Columbia United Kingdom *Hartley, Cumbria *Hartley, Plymou ...s. The ''entropy of Y conditioned on X'' is written as \Eta(Y, X). Definition The conditional entropy of Y given X is defined as where \mathcal X and \mathcal Y denote the support sets of X and Y. ''Note:'' Here, the convention is that the expression 0 \log 0 should be treated as being equal to zero. This is because \lim_ \theta\, \log \theta = 0. Intuitively, notice that by definition of Expected value, expected value and of Conditional Probability, conditional proba ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mutual Information
In quantum information theory, quantum mutual information, or von Neumann mutual information, after John von Neumann, is a measure of correlation between subsystems of quantum state. It is the quantum mechanical analog of Shannon mutual information. Motivation For simplicity, it will be assumed that all objects in the article are finite-dimensional. The definition of quantum mutual entropy is motivated by the classical case. For a probability distribution of two variables ''p''(''x'', ''y''), the two marginal distributions are :p(x) = \sum_ p(x,y), \qquad p(y) = \sum_ p(x,y). The classical mutual information ''I''(''X'':''Y'') is defined by :I(X:Y) = S(p(x)) + S(p(y)) - S(p(x,y)) where ''S''(''q'') denotes the Shannon entropy of the probability distribution ''q''. One can calculate directly :\begin S(p(x)) + S(p(y)) &= - \left (\sum_x p_x \log p(x) + \sum_y p_y \log p(y) \right ) \\ &= -\left (\sum_x \left ( \sum_ p(x,y') \log \sum_ p(x,y') \right ) + \sum_y \left ( \s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Quantum Entropy
The conditional quantum entropy is an entropy measure used in quantum information theory. It is a generalization of the conditional entropy of classical information theory. For a bipartite state \rho^, the conditional entropy is written S(A, B)_\rho, or H(A, B)_\rho, depending on the notation being used for the von Neumann entropy. The quantum conditional entropy was defined in terms of a conditional density operator \rho_ by Nicolas Cerf and Chris Adami, who showed that quantum conditional entropies can be negative, something that is forbidden in classical physics. The negativity of quantum conditional entropy is a sufficient criterion for quantum non-separability. In what follows, we use the notation S(\cdot) for the von Neumann entropy, which will simply be called "entropy". Definition Given a bipartite quantum state \rho^, the entropy of the joint system AB is S(AB)_\rho \ \stackrel\ S(\rho^), and the entropies of the subsystems are S(A)_\rho \ \stackrel\ S(\rho^A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
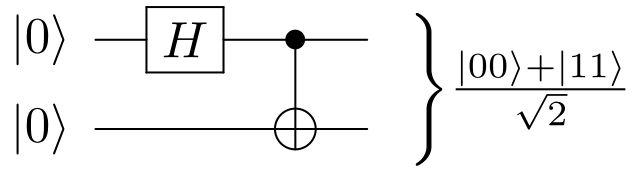
Bell State
The Bell states or EPR pairs are specific quantum states of two qubits that represent the simplest (and maximal) examples of quantum entanglement; conceptually, they fall under the study of quantum information science. The Bell states are a form of entangled and normalized basis vectors. This normalization implies that the overall probability of the particle being in one of the mentioned states is 1: \langle \Phi, \Phi \rangle = 1. Entanglement is a basis-independent result of superposition. Due to this superposition, measurement of the qubit will "collapse" it into one of its basis states with a given probability. Because of the entanglement, measurement of one qubit will "collapse" the other qubit to a state whose measurement will yield one of two possible values, where the value depends on which Bell state the two qubits are in initially. Bell states can be generalized to certain quantum states of multi-qubit systems, such as the GHZ state for 3 or more subsystems. Understand ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximally Entangled State
Quantum entanglement is the phenomenon that occurs when a group of particles are generated, interact, or share spatial proximity in a way such that the quantum state of each particle of the group cannot be described independently of the state of the others, including when the particles are separated by a large distance. The topic of quantum entanglement is at the heart of the disparity between classical and quantum physics: entanglement is a primary feature of quantum mechanics not present in classical mechanics. Measurements of physical properties such as position, momentum, spin, and polarization performed on entangled particles can, in some cases, be found to be perfectly correlated. For example, if a pair of entangled particles is generated such that their total spin is known to be zero, and one particle is found to have clockwise spin on a first axis, then the spin of the other particle, measured on the same axis, is found to be anticlockwise. However, this behavior gi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Entanglement
Quantum entanglement is the phenomenon that occurs when a group of particles are generated, interact, or share spatial proximity in a way such that the quantum state of each particle of the group cannot be described independently of the state of the others, including when the particles are separated by a large distance. The topic of quantum entanglement is at the heart of the disparity between classical and quantum physics: entanglement is a primary feature of quantum mechanics not present in classical mechanics. Measurements of physical properties such as position, momentum, spin, and polarization performed on entangled particles can, in some cases, be found to be perfectly correlated. For example, if a pair of entangled particles is generated such that their total spin is known to be zero, and one particle is found to have clockwise spin on a first axis, then the spin of the other particle, measured on the same axis, is found to be anticlockwise. However, this behavior gives ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Trace
In linear algebra and functional analysis, the partial trace is a generalization of the trace. Whereas the trace is a scalar valued function on operators, the partial trace is an operator-valued function. The partial trace has applications in quantum information and decoherence which is relevant for quantum measurement and thereby to the decoherent approaches to interpretations of quantum mechanics, including consistent histories and the relative state interpretation. Details Suppose V, W are finite-dimensional vector spaces over a field, with dimensions m and n, respectively. For any space A, let L(A) denote the space of linear operators on A. The partial trace over W is then written as \operatorname_W: \operatorname(V \otimes W) \to \operatorname(V). It is defined as follows: For T\in \operatorname(V \otimes W), let e_1, \ldots, e_m , and f_1, \ldots, f_n , be bases for ''V'' and ''W'' respectively; then ''T'' has a matrix representation : \ \quad 1 \leq k, i \leq m, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |