|
Jyā, Koti-jyā And Utkrama-jyā
Jyā, koṭi-jyā and utkrama-jyā are three trigonometric functions introduced by Indian mathematicians and astronomers. The earliest known Indian treatise containing references to these functions is Surya Siddhanta. These are functions of arcs of circles and not functions of angles. Jyā and koti-jyā are closely related to the modern trigonometric functions of sine and cosine. In fact, the origins of the modern terms of "sine" and "cosine" have been traced back to the Sanskrit words jyā and koti-jyā. Definition Let 'arc AB' denote an arc whose two extremities are A and B of a circle with center O. If a perpendicular BM be dropped from B to OA, then: * ''jyā'' of arc AB = BM * ''koti-jyā'' of arc AB = OM * ''utkrama-jyā'' of arc AB = MA If the radius of the circle is ''R'' and the length of arc AB is ''s'', the angle subtended by arc AB at O measured in radians is θ = ''s'' / ''R''. The three Indian functions are related to modern trigonometric functions as f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometric Functions
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent. Their reciprocals are respectively the cosecant, the secant, and the cotangent, which are less used. Each of these six trigonometric functions has a corresponding inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related to right-angle triangles, define them only for acute angles. To extend the sine and cos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cathetus
In a right triangle, a cathetus (originally from the Greek language, Greek word ; plural: catheti), commonly known as a leg, is either of the sides that are adjacent to the right angle. It is occasionally called a "side about the right angle". The side opposite the right angle is the hypotenuse. In the context of the hypotenuse, the catheti are sometimes referred to simply as "the other two sides". If the catheti of a right triangle have equal lengths, the triangle is isosceles. If they have different lengths, a distinction can be made between the minor (shorter) and major (longer) cathetus. The ratio of the lengths of the catheti defines the trigonometric functions tangent and cotangent of the acute angles in the triangle: the ratio c_1/c_2 is the tangent of the acute angle adjacent to c_2 and is also the cotangent of the acute angle adjacent to c_1. In a right triangle, the length of a cathetus is the geometric mean of the length of the adjacent segment cut by the altitude ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometry
Trigonometry () is a branch of mathematics that studies relationships between side lengths and angles of triangles. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. The Greeks focused on the calculation of chords, while mathematicians in India created the earliest-known tables of values for trigonometric ratios (also called trigonometric functions) such as sine. Throughout history, trigonometry has been applied in areas such as geodesy, surveying, celestial mechanics, and navigation. Trigonometry is known for its many identities. These trigonometric identities are commonly used for rewriting trigonometrical expressions with the aim to simplify an expression, to find a more useful form of an expression, or to solve an equation. History Sumerian astronomers studied angle measure, using a division of circles into 360 degrees. They, and later the Babylonians, studied the ratios of the sides of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometric Functions
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent. Their reciprocals are respectively the cosecant, the secant, and the cotangent, which are less used. Each of these six trigonometric functions has a corresponding inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related to right-angle triangles, define them only for acute angles. To extend the sine and cos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robert Of Chester
Robert of Chester (Latin: ''Robertus Castrensis'') was an English Arabist of the 12th century. He translated several historically important books from Arabic to Latin, such as: * '' The Book of the Composition of Alchemy'' (''Liber de compositione alchemiae''): translated in 1144, this was the first book on alchemy to become available in Europe *'''' (''Liber algebrae et almucabola''): |
Muḥammad Ibn Mūsā Al-Khwārizmī
Muhammad ( ar, مُحَمَّد; 570 – 8 June 632 CE) was an Arab religious, social, and political leader and the founder of Islam. According to Islamic doctrine, he was a prophet divinely inspired to preach and confirm the monotheistic teachings of Adam, Abraham, Moses, Jesus, and other prophets. He is believed to be the Seal of the Prophets within Islam. Muhammad united Arabia into a single Muslim polity, with the Quran as well as his teachings and practices forming the basis of Islamic religious belief. Muhammad was born approximately 570CE in Mecca. He was the son of Abdullah ibn Abd al-Muttalib and Amina bint Wahb. His father Abdullah was the son of Quraysh tribal leader Abd al-Muttalib ibn Hashim, and he died a few months before Muhammad's birth. His mother Amina died when he was six, leaving Muhammad an orphan. He was raised under the care of his grandfather, Abd al-Muttalib, and paternal uncle, Abu Talib. In later years, he would periodically seclu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gerard Of Cremona
Gerard of Cremona (Latin: ''Gerardus Cremonensis''; c. 1114 – 1187) was an Italian translator of scientific books from Arabic into Latin. He worked in Toledo, Kingdom of Castile and obtained the Arabic books in the libraries at Toledo. Some of the books had been originally written in Greek and, although well known in Byzantine Constantinople and Greece at the time, were unavailable in Greek or Latin in Western Europe. Gerard of Cremona is the most important translator among the Toledo School of Translators who invigorated Western medieval Europe in the twelfth century by transmitting the Arabs' and ancient Greeks' knowledge in astronomy, medicine and other sciences, by making the knowledge available in Latin. One of Gerard's most famous translations is of Ptolemy's ''Almagest'' from Arabic texts found in Toledo. Confusingly there appear to have been two translators of Arabic text into Latin known as ''Gerard of Cremona'', the one active in the 12th century who concentrated on a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Al-Battani
Abū ʿAbd Allāh Muḥammad ibn Jābir ibn Sinān al-Raqqī al-Ḥarrānī aṣ-Ṣābiʾ al-Battānī ( ar, محمد بن جابر بن سنان البتاني) ( Latinized as Albategnius, Albategni or Albatenius) (c. 858 – 929) was an astronomer and mathematician from Harran. He introduced a number of trigonometric relations, and his ''Kitāb az-Zīj'' was frequently quoted by many medieval astronomers, including Copernicus. Often called the "Ptolemy of the Arabs", al-Battani is perhaps one of the greatest and best known astronomer of the medieval Islamic world. Life Little of al-Battānī's life is known other than his birthplace in Harran near Urfa, in Upper Mesopotamia, (today in Turkey) and his father's fame as a maker of scientific instruments. Jabir ibn Sinan al-Harrani was likely this famous instrument maker, although this is not something that has been proven. His epithet ''aṣ-Ṣabi’'' suggests that his family belonged to the Sabian religion of Harran, an obscur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plato Tiburtinus
Plato Tiburtinus ( la, Plato Tiburtinus, "Plato of Tivoli"; fl. 12th century) was a 12th-century Italian mathematician, astronomer and translator who lived in Barcelona from 1116 to 1138. He is best known for translating Hebrew and Arabic documents into Latin, and was apparently the first to translate information on the astrolabe (an astronomical instrument) from Arabic. Plato of Tivoli translated the Arab astrologer Albohali's "Book of Birth" into Latin in 1136. He translated Claudius Ptolemy's Tetrabiblos from Arabic to Latin in 1138, the astronomical works of al-Battani, Theodosius' ''Spherics'' and the ''Liber Embadorum'' by Abraham bar Chiia.David Eugene Smith, ''History of Mathematics'', (Dover Publications, Inc, 1951), 201. He has worked together with the Jewish mathematician Savasorda ( Abraham Bar Ḥiyya Ha-Nasi). His manuscripts were widely circulated and were among others used by Albertus Magnus and Fibonacci. Works To him are attributed four works in science-math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sinus
Sinus may refer to: Anatomy * Sinus (anatomy), a sac or cavity in any organ or tissue ** Paranasal sinuses, air cavities in the cranial bones, especially those near the nose, including: *** Maxillary sinus, is the largest of the paranasal sinuses, under the eyes, in the maxillary bones *** Frontal sinus, superior to the eyes, in the frontal bone, which forms the hard part of the forehead *** Ethmoid sinus, formed from several discrete air cells within the ethmoid bone between the eyes and under the nose *** Sphenoidal sinus, in the sphenoid bone at the center of the skull base under the pituitary gland ** Anal sinuses, the furrows which separate the columns in the rectum ** Dural venous sinuses, venous channels found between layers of dura mater in the brain * Sinus (botany), a space or indentation, usually on a leaf Heart * Sinus node, a structure in the superior part of the right atrium * Sinus rhythm, normal beating on an ECG * Coronary sinus, a vein collecting blood from the he ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Medieval Latin
Medieval Latin was the form of Literary Latin used in Roman Catholic Western Europe during the Middle Ages. In this region it served as the primary written language, though local languages were also written to varying degrees. Latin functioned as the main medium of scholarly exchange, as the liturgical language of the Church, and as the working language of science, literature, law, and administration. Medieval Latin represented a continuation of Classical Latin and Late Latin, with enhancements for new concepts as well as for the increasing integration of Christianity. Despite some meaningful differences from Classical Latin, Medieval writers did not regard it as a fundamentally different language. There is no real consensus on the exact boundary where Late Latin ends and Medieval Latin begins. Some scholarly surveys begin with the rise of early Ecclesiastical Latin in the middle of the 4th century, others around 500, and still others with the replacement of written Late Latin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
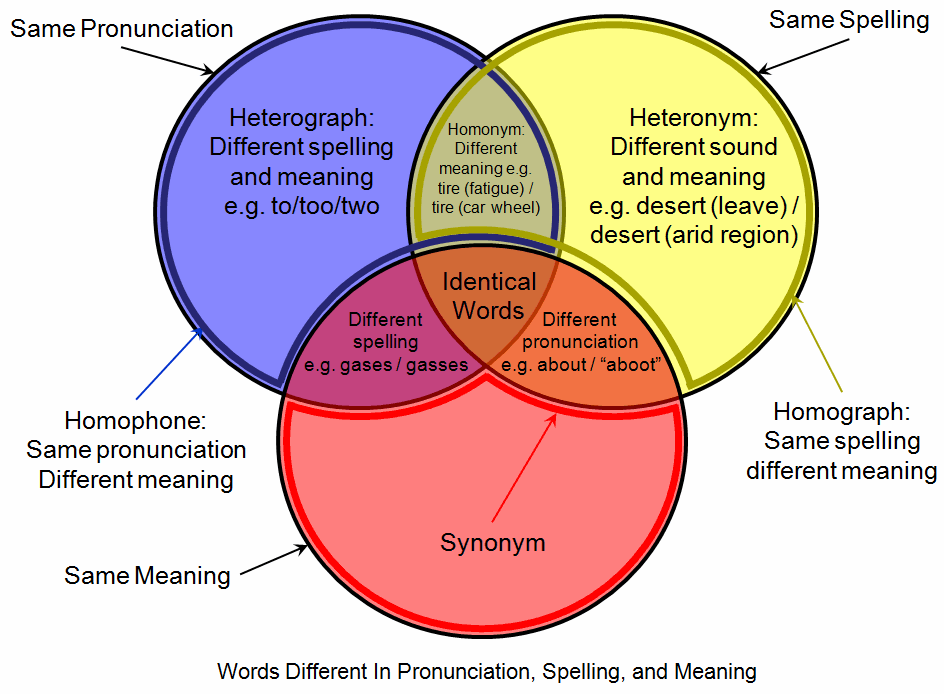
Homograph
A homograph (from the el, ὁμός, ''homós'', "same" and γράφω, ''gráphō'', "write") is a word that shares the same written form as another word but has a different meaning. However, some dictionaries insist that the words must also be pronounced differently, while the Oxford English Dictionary says that the words should also be of "different origin". In this vein, ''The Oxford Guide to Practical Lexicography'' lists various types of homographs, including those in which the words are discriminated by being in a different ''word class'', such as ''hit'', the verb ''to strike'', and ''hit'', the noun ''a blow''. If, when spoken, the meanings may be distinguished by different pronunciations, the words are also heteronyms. Words with the same writing ''and'' pronunciation (i.e. are both homographs and homophones) are considered homonyms. However, in a looser sense the term "homonym" may be applied to words with the same writing ''or'' pronunciation. Homograph disambiguat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
