|
Infinitely Divisible
Infinite divisibility arises in different ways in philosophy, physics, economics, order theory (a branch of mathematics), and probability theory (also a branch of mathematics). One may speak of infinite divisibility, or the lack thereof, of matter, space, time, money, or abstract mathematical objects such as the continuum. In philosophy The origin of the idea in the Western tradition can be traced to the 5th century BCE starting with the Ancient Greek pre-Socratic philosopher Democritus and his teacher Leucippus, who theorized matter's divisibility beyond what can be perceived by the senses until ultimately ending at an indivisible atom. The Indian philosopher, Maharshi Kanada also proposed an atomistic theory, however there is ambiguity around when this philosopher lived, ranging from sometime between the 6th century to 2nd century BCE. Around 500 BC, he postulated that if we go on dividing matter ('' padarth''), we shall get smaller and smaller particles. Ultimately, a time wil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Philosophy
Philosophy (from , ) is the systematized study of general and fundamental questions, such as those about existence, reason, knowledge, values, mind, and language. Such questions are often posed as problems to be studied or resolved. Some sources claim the term was coined by Pythagoras ( BCE), although this theory is disputed by some. Philosophical methods include questioning, critical discussion, rational argument, and systematic presentation. in . Historically, ''philosophy'' encompassed all bodies of knowledge and a practitioner was known as a ''philosopher''."The English word "philosophy" is first attested to , meaning "knowledge, body of knowledge." "natural philosophy," which began as a discipline in ancient India and Ancient Greece, encompasses astronomy, medicine, and physics. For example, Newton's 1687 ''Mathematical Principles of Natural Philosophy'' later became classified as a book of physics. In the 19th century, the growth of modern research universiti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Timaeus (dialogue)
''Timaeus'' (; grc-gre, Τίμαιος, Timaios, ) is one of Plato's dialogues, mostly in the form of long monologues given by Critias and Timaeus, written 360 BC. The work puts forward reasoning on the possible nature of the physical world and human beings and is followed by the dialogue ''Critias''. Participants in the dialogue include Socrates, Timaeus, Hermocrates, and Critias. Some scholars believe that it is not the Critias of the Thirty Tyrants who appears in this dialogue, but his grandfather, who is also named Critias. It has been suggested from some traditions (Diogenes Laertius (VIII 85) from Hermippus of Smyrna (3rd century BC) and Timon of Phlius ( 320 – 235 BC)) that ''Timaeus'' was influenced by a book about Pythagoras, written by Philolaus, although this assertion is generally considered false. Introduction The dialogue takes place the day after Socrates described his ideal state. In Plato's works, such a discussion occurs in the ''Republic''. Socrates fe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quark
A quark () is a type of elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. All commonly observable matter is composed of up quarks, down quarks and electrons. Owing to a phenomenon known as ''color confinement'', quarks are never found in isolation; they can be found only within hadrons, which include baryons (such as protons and neutrons) and mesons, or in quark–gluon plasmas. There is also the theoretical possibility of more exotic phases of quark matter. For this reason, much of what is known about quarks has been drawn from observations of hadrons. Quarks have various intrinsic properties, including electric charge, mass, color charge, and spin. They are the only elementary particles in the Standard Model of particle physics to experience all four fundamental interactions, also known as ''fundamental forces'' (electro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Model
The Standard Model of particle physics is the theory describing three of the four known fundamental forces (electromagnetism, electromagnetic, weak interaction, weak and strong interactions - excluding gravity) in the universe and classifying all known elementary particles. It was developed in stages throughout the latter half of the 20th century, through the work of many scientists worldwide, with the current formulation being finalized in the mid-1970s upon experimental confirmation of the existence of quarks. Since then, proof of the top quark (1995), the tau neutrino (2000), and the Higgs boson (2012) have added further credence to the Standard Model. In addition, the Standard Model has predicted various properties of weak neutral currents and the W and Z bosons with great accuracy. Although the Standard Model is believed to be theoretically self-consistent and has demonstrated huge successes in providing experimental predictions, it leaves some physics beyond the standard m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logic
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the science of deductively valid inferences or of logical truths. It is a formal science investigating how conclusions follow from premises in a topic-neutral way. When used as a countable noun, the term "a logic" refers to a logical formal system that articulates a proof system. Formal logic contrasts with informal logic, which is associated with informal fallacies, critical thinking, and argumentation theory. While there is no general agreement on how formal and informal logic are to be distinguished, one prominent approach associates their difference with whether the studied arguments are expressed in formal or informal languages. Logic plays a central role in multiple fields, such as philosophy, mathematics, computer science, and linguistics. Logic studies arguments, which consist of a set of premises together with a conclusion. Premises and conclusions are usually un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partition Of A Set
In mathematics, a partition of a set is a grouping of its elements into non-empty subsets, in such a way that every element is included in exactly one subset. Every equivalence relation on a set defines a partition of this set, and every partition defines an equivalence relation. A set equipped with an equivalence relation or a partition is sometimes called a setoid, typically in type theory and proof theory. Definition and Notation A partition of a set ''X'' is a set of non-empty subsets of ''X'' such that every element ''x'' in ''X'' is in exactly one of these subsets (i.e., ''X'' is a disjoint union of the subsets). Equivalently, a family of sets ''P'' is a partition of ''X'' if and only if all of the following conditions hold: *The family ''P'' does not contain the empty set (that is \emptyset \notin P). *The union of the sets in ''P'' is equal to ''X'' (that is \textstyle\bigcup_ A = X). The sets in ''P'' are said to exhaust or cover ''X''. See also collectively exhaus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ad Infinitum
''Ad infinitum'' is a Latin phrase meaning "to infinity" or "forevermore". Description In context, it usually means "continue forever, without limit" and this can be used to describe a non-terminating process, a non-terminating ''repeating'' process, or a set of instructions to be repeated "forever," among other uses. It may also be used in a manner similar to the Latin phrase ''et cetera'' to denote written words or a concept that continues for a lengthy period beyond what is shown. Examples include: * "The sequence 1, 2, 3, ... continues ''ad infinitum''." * "The perimeter of a fractal may be iteratively drawn ''ad infinitum''." The 17th-century writer Jonathan Swift incorporated the idea of self-similarity in the following lines from his satirical poem ''On Poetry: a Rhapsody'' (1733): The vermin only teaze and pinch Their foes superior by an inch. So, naturalists observe, a flea Has smaller fleas that on him prey; And these have smaller still to bite 'em, And so proceed ''ad ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary (macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limits to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Process And Reality
''Process and Reality'' is a book by Alfred North Whitehead, in which the author propounds a philosophy of organism, also called process philosophy. The book, published in 1929, is a revision of the Gifford Lectures he gave in 1927–28. Whitehead's ''Process and Reality'' Whitehead's background was an unusual one for a speculative philosopher. Educated as a mathematician, he became, through his coauthorship with his student and disciple Bertrand Russell and publication in 1913 of ''Principia Mathematica'', a major logician. Later he wrote extensively on physics and its philosophy, proposing a theory of gravity in Minkowski space as a logically possible alternative to Einstein's general theory of relativity. Whitehead's ''Process and Reality''Whitehead, A.N. (1929). ''Process and Reality. An Essay in Cosmology. Gifford Lectures Delivered in the University of Edinburgh During the Session 1927–1928'', Macmillan, New York, Cambridge University Press, Cambridge UK. is perhaps his ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alfred North Whitehead
Alfred North Whitehead (15 February 1861 – 30 December 1947) was an English mathematician and philosopher. He is best known as the defining figure of the philosophical school known as process philosophy, which today has found application to a wide variety of disciplines, including ecology, theology, education, physics, biology, economics, and psychology, among other areas. In his early career Whitehead wrote primarily on mathematics, logic, and physics. His most notable work in these fields is the three-volume ''Principia Mathematica'' (1910–1913), which he wrote with former student Bertrand Russell. ''Principia Mathematica'' is considered one of the twentieth century's most important works in mathematical logic, and placed 23rd in a list of the top 100 English-language nonfiction books of the twentieth century by Modern Library. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
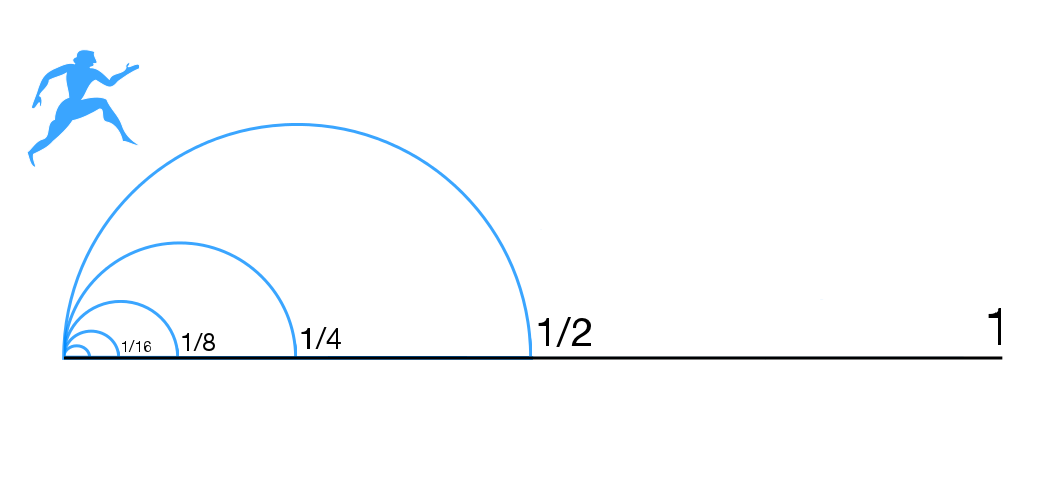
Zeno's Paradoxes
Zeno's paradoxes are a set of philosophical problems generally thought to have been devised by Greek philosopher Zeno of Elea (c. 490–430 BC) to support Parmenides' doctrine that contrary to the evidence of one's senses, the belief in plurality and change is mistaken, and in particular that motion is nothing but an illusion. It is usually assumed, based on Plato's ''Parmenides'' (128a–d), that Zeno took on the project of creating these paradoxes because other philosophers had created paradoxes against Parmenides' view. Thus Plato has Zeno say the purpose of the paradoxes "is to show that their hypothesis that existences are many, if properly followed up, leads to still more absurd results than the hypothesis that they are one." Plato has Socrates claim that Zeno and Parmenides were essentially arguing exactly the same point. Some of Zeno's nine surviving paradoxes (preserved in Aristotle's ''Physics'' [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extended Item
Extension, extend or extended may refer to: Mathematics Logic or set theory * Axiom of extensionality * Extensible cardinal * Extension (model theory) * Extension (predicate logic), the set of tuples of values that satisfy the predicate * Extension (semantics), the set of things to which a property applies * Extension by definitions * Extensional definition, a definition that enumerates every individual a term applies to * Extensionality Other uses * Extension of a polyhedron, in geometry * Exterior algebra, Grassmann's theory of extension, in geometry * Homotopy extension property, in topology * Kolmogorov extension theorem, in probability theory * Linear extension, in order theory * Sheaf extension, in algebraic geometry * Tietze extension theorem, in topology * Whitney extension theorem, in differential geometry * Group extension, in abstract algebra and homological algebra Music * Extension (music), notes that fit outside the standard range * ''Extended'' (Solar Fields a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |