|
Incremental Deformations
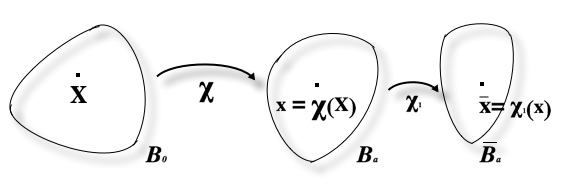
In solid mechanics, the linear stability analysis of an elastic solution is studied using the method of incremental deformations superposed on finite deformations. The method of incremental deformation can be used to solve static, quasi-static and time-dependent problems. The governing equations of the motion are ones of the classical mechanics, such as the conservation of mass and the balance of linear and angular momentum, which provide the equilibrium configuration of the material. The main corresponding mathematical framework is described in the main Raymond Ogden's book ''Non-linear elastic deformations'' and in Biot's book ''Mechanics of incremental deformations'', which is a collection of his main papers. Nonlinear Elasticity Kinematics and Mechanics Let \mathcal \in \mathbb^3 be a three-dimensional Euclidean space. Let \mathcal_0, \mathcal_a \in \mathcal be two regions occupied by the material in two different instants of time. Let be the deformation which transfor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid Mechanics
Solid mechanics, also known as mechanics of solids, is the branch of continuum mechanics that studies the behavior of solid materials, especially their motion and deformation under the action of forces, temperature changes, phase changes, and other external or internal agents. Solid mechanics is fundamental for civil, aerospace, nuclear, biomedical and mechanical engineering, for geology, and for many branches of physics such as materials science. It has specific applications in many other areas, such as understanding the anatomy of living beings, and the design of dental prostheses and surgical implants. One of the most common practical applications of solid mechanics is the Euler–Bernoulli beam equation. Solid mechanics extensively uses tensors to describe stresses, strains, and the relationship between them. Solid mechanics is a vast subject because of the wide range of solid materials available, such as steel, wood, concrete, biological materials, textiles, geological ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperelastic Material
A hyperelastic or Green elastic materialR.W. Ogden, 1984, ''Non-Linear Elastic Deformations'', , Dover. is a type of constitutive model for ideally elastic material for which the stress–strain relationship derives from a strain energy density function. The hyperelastic material is a special case of a Cauchy elastic material. For many materials, linear elastic models do not accurately describe the observed material behaviour. The most common example of this kind of material is rubber, whose stress-strain relationship can be defined as non-linearly elastic, isotropic and incompressible. Hyperelasticity provides a means of modeling the stress–strain behavior of such materials. The behavior of unfilled, vulcanized elastomers often conforms closely to the hyperelastic ideal. Filled elastomers and biological tissues are also often modeled via the hyperelastic idealization. Ronald Rivlin and Melvin Mooney developed the first hyperelastic models, the Neo-Hookean and Mooney–Ri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Instability Analysis
In numerous fields of study, the component of instability within a system is generally characterized by some of the outputs or internal states growing without bounds. Not all systems that are not stable are unstable; systems can also be marginally stable or exhibit limit cycle behavior. In structural engineering, a structure can become unstable when excessive load is applied. Beyond a certain threshold, structural deflections magnify stresses, which in turn increases deflections. This can take the form of buckling or crippling. The general field of study is called structural stability. Atmospheric instability is a major component of all weather systems on Earth. Instability in control systems In the theory of dynamical systems, a state variable in a system is said to be unstable if it evolves without bounds. A system itself is said to be unstable if at least one of its state variables is unstable. In continuous time control theory, a system is unstable if any of the ro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
First-order Partial Differential Equation
In mathematics, a first-order partial differential equation is a partial differential equation that involves only first derivatives of the unknown function of ''n'' variables. The equation takes the form : F(x_1,\ldots,x_n,u,u_,\ldots u_) =0. \, Such equations arise in the construction of characteristic surfaces for hyperbolic partial differential equations, in the calculus of variations, in some geometrical problems, and in simple models for gas dynamics whose solution involves the method of characteristics. If a family of solutions of a single first-order partial differential equation can be found, then additional solutions may be obtained by forming envelopes of solutions in that family. In a related procedure, general solutions may be obtained by integrating families of ordinary differential equations. General solution and complete integral The ''general solution'' to the first order partial differential equation is a solution which contains an arbitrary function. But, the sol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equation
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a Multivariable calculus, multivariable function. The function is often thought of as an "unknown" to be solved for, similarly to how is thought of as an unknown number to be solved for in an algebraic equation like . However, it is usually impossible to write down explicit formulas for solutions of partial differential equations. There is, correspondingly, a vast amount of modern mathematical and scientific research on methods to Numerical methods for partial differential equations, numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematics, pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Incompressible Flow
In fluid mechanics or more generally continuum mechanics, incompressible flow ( isochoric flow) refers to a flow in which the material density is constant within a fluid parcel—an infinitesimal volume that moves with the flow velocity. An equivalent statement that implies incompressibility is that the divergence of the flow velocity is zero (see the derivation below, which illustrates why these conditions are equivalent). Incompressible flow does not imply that the fluid itself is incompressible. It is shown in the derivation below that (under the right conditions) even compressible fluids can – to a good approximation – be modelled as an incompressible flow. Incompressible flow implies that the density remains constant within a parcel of fluid that moves with the flow velocity. Derivation The fundamental requirement for incompressible flow is that the density, \rho , is constant within a small element volume, ''dV'', which moves at the flow velocity u. Mathematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boundary Value Problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional constraints, called the boundary conditions. A solution to a boundary value problem is a solution to the differential equation which also satisfies the boundary conditions. Boundary value problems arise in several branches of physics as any physical differential equation will have them. Problems involving the wave equation, such as the determination of normal modes, are often stated as boundary value problems. A large class of important boundary value problems are the Sturm–Liouville problems. The analysis of these problems involves the eigenfunctions of a differential operator. To be useful in applications, a boundary value problem should be well posed. This means that given the input to the problem there exists a unique solution, which depends continuously on the input. Much theoretical work in the field of partial differential ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volume
Volume is a measure of occupied three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch). The definition of length (cubed) is interrelated with volume. The volume of a container is generally understood to be the capacity of the container; i.e., the amount of fluid (gas or liquid) that the container could hold, rather than the amount of space the container itself displaces. In ancient times, volume is measured using similar-shaped natural containers and later on, standardized containers. Some simple three-dimensional shapes can have its volume easily calculated using arithmetic formulas. Volumes of more complicated shapes can be calculated with integral calculus if a formula exists for the shape's boundary. Zero-, one- and two-dimensional objects have no volume; in fourth and higher dimensions, an analogous concept to the normal vo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the quantity of the vector field's source at each point. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around a given point. As an example, consider air as it is heated or cooled. The velocity of the air at each point defines a vector field. While air is heated in a region, it expands in all directions, and thus the velocity field points outward from that region. The divergence of the velocity field in that region would thus have a positive value. While the air is cooled and thus contracting, the divergence of the velocity has a negative value. Physical interpretation of divergence In physical terms, the divergence of a vector field is the extent to which the vector field flux behaves like a source at a given point. It is a local measure of its "outgoingness" – the extent to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Body Force
In physics, a body force is a force that acts throughout the volume of a body. Springer site - Book 'Solid mechanics'preview paragraph 'Body forces'./ref> Forces due to gravity, electric fields and magnetic fields are examples of body forces. Body forces contrast with contact forces or surface forces which are exerted to the surface of an object. Normal forces and shear forces between objects are surface forces as they are exerted to the surface of an object. All cohesive surface attraction and contact forces between objects are also considered as surface forces. Fictitious forces such as the centrifugal force, Euler force, and the Coriolis effect are other examples of body forces. Definition Qualitative A body force is simply a type of force, and so it has the same dimensions as force, L] sup>−2. However, it is often convenient to talk about a body force in terms of either the force per unit volume or the force per unit mass. If the force per unit volume is of interest, i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stress (mechanics)
In continuum mechanics, stress is a physical quantity. It is a quantity that describes the magnitude of forces that cause deformation. Stress is defined as ''force per unit area''. When an object is pulled apart by a force it will cause elongation which is also known as deformation, like the stretching of an elastic band, it is called tensile stress. But, when the forces result in the compression of an object, it is called compressive stress. It results when forces like tension or compression act on a body. The greater this force and the smaller the cross-sectional area of the body on which it acts, the greater the stress. Therefore, stress is measured in newton per square meter (N/m2) or pascal (Pa). Stress expresses the internal forces that neighbouring particles of a continuous material exert on each other, while strain is the measure of the deformation of the material. For example, when a solid vertical bar is supporting an overhead weight, each particle in the bar pushe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Strain Theory
In continuum mechanics, the finite strain theory—also called large strain theory, or large deformation theory—deals with deformations in which strains and/or rotations are large enough to invalidate assumptions inherent in infinitesimal strain theory. In this case, the undeformed and deformed configurations of the continuum are significantly different, requiring a clear distinction between them. This is commonly the case with elastomers, plastically-deforming materials and other fluids and biological soft tissue. Displacement The displacement of a body has two components: a rigid-body displacement and a deformation. * A rigid-body displacement consists of a simultaneous translation (physics) and rotation of the body without changing its shape or size. * Deformation implies the change in shape and/or size of the body from an initial or undeformed configuration \kappa_0(\mathcal B) to a current or deformed configuration \kappa_t(\mathcal B) (Figure 1). A change in the conf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg)

