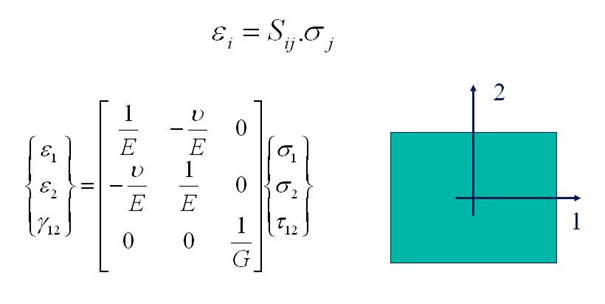|
Impulse Excitation Technique
The impulse excitation technique (IET) is a non-destructive material characterization technique to determine the elastic properties and internal friction of a material of interest. It measures the resonant frequencies in order to calculate the Young's modulus, shear modulus, Poisson's ratio and internal friction of predefined shapes like rectangular bars, cylindrical rods and disc shaped samples. The measurements can be performed at room temperature or at elevated temperatures (up to 1700 °C) under different atmospheres. The measurement principle is based on tapping the sample with a small projectile and recording the induced vibration signal with a piezoelectric sensor, microphone, laser vibrometer or accelerometer. To optimize the results a microphone or a laser vibrometer can be used as there is no contact between the test-piece and the sensor. Laser vibrometers are preferred to measure signals in vacuum. Afterwards, the acquired vibration signal in the time domain is conv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Frequency
The fundamental frequency, often referred to simply as the ''fundamental'', is defined as the lowest frequency of a periodic waveform. In music, the fundamental is the musical pitch of a note that is perceived as the lowest partial present. In terms of a superposition of sinusoids, the fundamental frequency is the lowest frequency sinusoidal in the sum of harmonically related frequencies, or the frequency of the difference between adjacent frequencies. In some contexts, the fundamental is usually abbreviated as 0, indicating the lowest frequency counting from zero. In other contexts, it is more common to abbreviate it as 1, the first harmonic. (The second harmonic is then 2 = 2⋅1, etc. In this context, the zeroth harmonic would be 0 Hz.) According to Benward's and Saker's ''Music: In Theory and Practice'': Explanation All sinusoidal and many non-sinusoidal waveforms repeat exactly over time – they are periodic. The period of a waveform is the smallest value of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isotropy
Isotropy is uniformity in all orientations; it is derived . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence ''anisotropy''. ''Anisotropy'' is also used to describe situations where properties vary systematically, dependent on direction. Isotropic radiation has the same intensity regardless of the direction of measurement, and an isotropic field exerts the same action regardless of how the test particle is oriented. Mathematics Within mathematics, ''isotropy'' has a few different meanings: ; Isotropic manifolds: A manifold is isotropic if the geometry on the manifold is the same regardless of direction. A similar concept is homogeneity. ; Isotropic quadratic form: A quadratic form ''q'' is said to be isotropic if there is a non-zero vector ''v'' such that ; such a ''v'' is an isotropic vector or null vector. In complex geometry, a line through the origin in the direction of an isotropic vector is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthotropic Material
In material science and solid mechanics, orthotropic materials have material properties at a particular point which differ along three orthogonal axes, where each axis has twofold rotational symmetry. These directional differences in strength can be quantified with Hankinson's equation. They are a subset of anisotropy, anisotropic materials, because their properties change when measured from different directions. A familiar example of an orthotropic material is wood. In wood, one can define three mutually perpendicular directions at each point in which the properties are different. It is most stiff (and strong) along the grain, because most cellulose fibrils are aligned that way. It is usually least stiff in the radial direction (between the growth rings), and is intermediate in the circumferential direction. This anisotropy was provided by evolution, as it best enables the tree to remain upright. Because the preferred coordinate system is cylindrical-polar, this type of orthotrop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isotropic Stress Strain Relation
Isotropy is uniformity in all orientations; it is derived . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence '' anisotropy''. ''Anisotropy'' is also used to describe situations where properties vary systematically, dependent on direction. Isotropic radiation has the same intensity regardless of the direction of measurement, and an isotropic field exerts the same action regardless of how the test particle is oriented. Mathematics Within mathematics, ''isotropy'' has a few different meanings: ; Isotropic manifolds: A manifold is isotropic if the geometry on the manifold is the same regardless of direction. A similar concept is homogeneity. ; Isotropic quadratic form: A quadratic form ''q'' is said to be isotropic if there is a non-zero vector ''v'' such that ; such a ''v'' is an isotropic vector or null vector. In complex geometry, a line through the origin in the direction of an isotropic vect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poisson’s Ratio
In materials science and solid mechanics, Poisson's ratio \nu ( nu) is a measure of the Poisson effect, the deformation (expansion or contraction) of a material in directions perpendicular to the specific direction of loading. The value of Poisson's ratio is the negative of the ratio of transverse strain to axial strain. For small values of these changes, \nu is the amount of transversal elongation divided by the amount of axial compression. Most materials have Poisson's ratio values ranging between 0.0 and 0.5. For soft materials, such as rubber, where the bulk modulus is much higher than the shear modulus, Poisson's ratio is near 0.5. For open-cell polymer foams, Poisson's ratio is near zero, since the cells tend to collapse in compression. Many typical solids have Poisson's ratios in the range of 0.2–0.3. The ratio is named after the French mathematician and physicist Siméon Poisson. Origin Poisson's ratio is a measure of the Poisson effect, the phenomenon in which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Young’s Modulus
Young's modulus E, the Young modulus, or the modulus of elasticity in tension or compression (i.e., negative tension), is a mechanical property that measures the tensile or compressive stiffness of a solid material when the force is applied lengthwise. It quantifies the relationship between tensile/compressive stress \sigma (force per unit area) and axial strain \varepsilon (proportional deformation) in the linear elastic region of a material and is determined using the formula: E = \frac Young's moduli are typically so large that they are expressed not in pascals but in gigapascals (GPa). Example: * Silly Putty (increasing pressure: length increases quickly, meaning tiny E) * Aluminum (increasing pressure: length increases slowly, meaning high E) Higher Young's modulus corresponds to greater (lengthwise) stiffness. Although Young's modulus is named after the 19th-century British scientist Thomas Young, the concept was developed in 1727 by Leonhard Euler. The firs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isotropic
Isotropy is uniformity in all orientations; it is derived . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence ''anisotropy''. ''Anisotropy'' is also used to describe situations where properties vary systematically, dependent on direction. Isotropic radiation has the same intensity regardless of the direction of measurement, and an isotropic field exerts the same action regardless of how the test particle is oriented. Mathematics Within mathematics, ''isotropy'' has a few different meanings: ; Isotropic manifolds: A manifold is isotropic if the geometry on the manifold is the same regardless of direction. A similar concept is homogeneity. ; Isotropic quadratic form: A quadratic form ''q'' is said to be isotropic if there is a non-zero vector ''v'' such that ; such a ''v'' is an isotropic vector or null vector. In complex geometry, a line through the origin in the direction of an isotropic vector is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Damped Sin
Damping is an influence within or upon an oscillatory system that has the effect of reducing or preventing its oscillation. In physical systems, damping is produced by processes that dissipate the energy stored in the oscillation. Examples include viscous drag (a liquid's viscosity can hinder an oscillatory system, causing it to slow down; see viscous damping) in mechanical systems, resistance in electronic oscillators, and absorption and scattering of light in optical oscillators. Damping not based on energy loss can be important in other oscillating systems such as those that occur in biological systems and bikes (ex. Suspension (mechanics)). Not to be confused with friction, which is a dissipative force acting on a system. Friction can cause or be a factor of damping. The damping ratio is a dimensionless measure describing how oscillations in a system decay after a disturbance. Many systems exhibit oscillatory behavior when they are disturbed from their position of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quality Control
Quality control (QC) is a process by which entities review the quality of all factors involved in production. ISO 9000 defines quality control as "a part of quality management focused on fulfilling quality requirements". This approach places emphasis on three aspects (enshrined in standards such as ISO 9001): # Elements such as controls, job management, defined and well managed processes, performance and integrity criteria, and identification of records # Competence, such as knowledge, skills, experience, and qualifications # Soft elements, such as personnel, integrity, confidence, organizational culture, motivation, team spirit, and quality relationships. Inspection is a major component of quality control, where physical product is examined visually (or the end results of a service are analyzed). Product inspectors will be provided with lists and descriptions of unacceptable product defects such as cracks or surface blemishes for example. History and introduction Ea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Refractory
In materials science, a refractory material or refractory is a material that is resistant to decomposition by heat, pressure, or chemical attack, and retains strength and form at high temperatures. Refractories are polycrystalline, polyphase, inorganic, non-metallic, porous, and heterogeneous. They are typically composed of oxides or carbides, nitrides etc. of the following materials: silicon, aluminium, magnesium, calcium, boron, chromium and zirconium. ASTM C71 defines refractories as "...non-metallic materials having those chemical and physical properties that make them applicable for structures, or as components of systems, that are exposed to environments above ." Refractory materials are used in furnaces, kilns, incinerators, and reactors. Refractories are also used to make crucibles and moulds for casting glass and metals and for surfacing flame deflector systems for rocket launch structures. Today, the iron- and steel-industry and metal casting sectors use appr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ceramic Engineering
Ceramic engineering is the science and technology of creating objects from inorganic, non-metallic materials. This is done either by the action of heat, or at lower temperatures using precipitation reactions from high-purity chemical solutions. The term includes the purification of raw materials, the study and production of the chemical compounds concerned, their formation into components and the study of their structure, composition and properties. Ceramic materials may have a crystalline or partly crystalline structure, with long-range order on atomic scale. Glass ceramics may have an amorphous or glassy structure, with limited or short-range atomic order. They are either formed from a molten mass that solidifies on cooling, formed and matured by the action of heat, or chemically synthesized at low temperatures using, for example, hydrothermal or sol-gel synthesis. The special character of ceramic materials gives rise to many applications in materials engineering, electric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ultrasound Spectroscopy
Ultrasound is sound waves with frequencies higher than the upper audible limit of human hearing. Ultrasound is not different from "normal" (audible) sound in its physical properties, except that humans cannot hear it. This limit varies from person to person and is approximately 20 kilohertz (20,000 hertz) in healthy young adults. Ultrasound devices operate with frequencies from 20 kHz up to several gigahertz. Ultrasound is used in many different fields. Ultrasonic devices are used to detect objects and measure distances. Ultrasound imaging or sonography is often used in medicine. In the nondestructive testing of products and structures, ultrasound is used to detect invisible flaws. Industrially, ultrasound is used for cleaning, mixing, and accelerating chemical processes. Animals such as bats and porpoises use ultrasound for locating prey and obstacles. History Acoustics, the science of sound, starts as far back as Pythagoras in the 6th century BC, who wrote on t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |