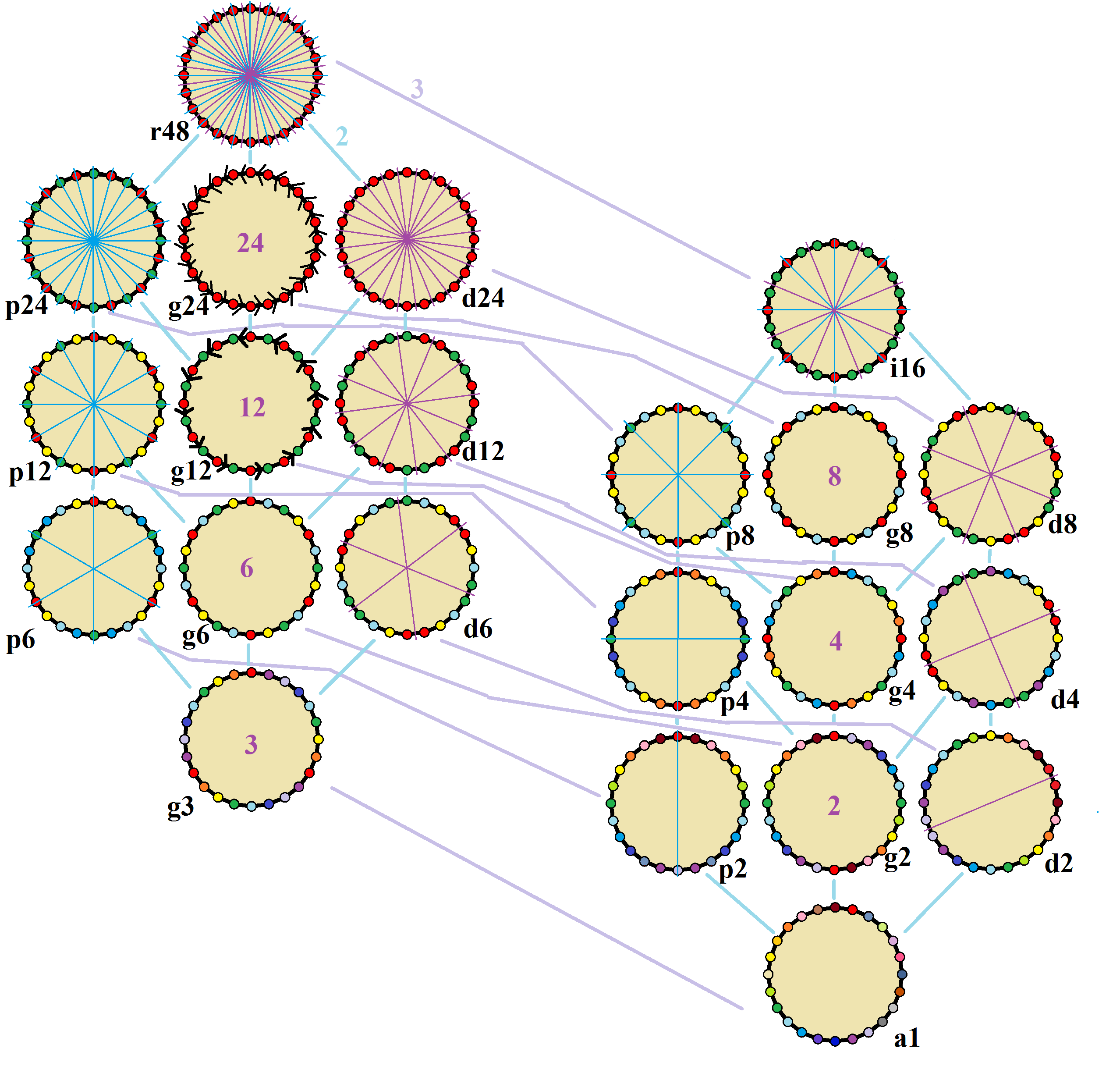
|
Icositetragon
In geometry, an icositetragon (or icosikaitetragon) or 24-gon is a twenty-four-sided polygon. The sum of any icositetragon's interior angles is 3960 degrees. Regular icositetragon The ''regular polygon, regular icositetragon'' is represented by Schläfli symbol and can also be constructed as a Truncation (geometry), truncated dodecagon, t, or a twice-truncated hexagon, tt, or thrice-truncated triangle, ttt. One interior angle in a regular polygon, regular icositetragon is 165°, meaning that one exterior angle would be 15°. The area of a regular icositetragon is: (with ''t'' = edge length) : A = 6t^2 \cot \frac = t^2(2+\sqrt+\sqrt+\sqrt). The icositetragon appeared in Archimedes' polygon approximation of pi, along with the hexagon (6-gon), dodecagon (12-gon), tetracontaoctagon (48-gon), and enneacontahexagon (96-gon). Construction As 24 = 23 × 3, a regular icositetragon is constructible polygon, constructible using an angle trisector. As a truncated dodecagon, it can be con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constructible Polygon
In mathematics, a constructible polygon is a regular polygon that can be constructed with compass and straightedge. For example, a regular pentagon is constructible with compass and straightedge while a regular heptagon is not. There are infinitely many constructible polygons, but only 31 with an odd number of sides are known. Conditions for constructibility Some regular polygons are easy to construct with compass and straightedge; others are not. The ancient Greek mathematicians knew how to construct a regular polygon with 3, 4, or 5 sides, and they knew how to construct a regular polygon with double the number of sides of a given regular polygon.Bold, Benjamin. ''Famous Problems of Geometry and How to Solve Them'', Dover Publications, 1982 (orig. 1969). This led to the question being posed: is it possible to construct ''all'' regular polygons with compass and straightedge? If not, which ''n''-gons (that is, polygons with ''n'' edges) are constructible and which are not? Carl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either convex polygon, convex, star polygon, star or Skew polygon, skew. In the limit (mathematics), limit, a sequence of regular polygons with an increasing number of sides approximates a circle, if the perimeter or area is fixed, or a regular apeirogon (effectively a Line (geometry), straight line), if the edge length is fixed. General properties ''These properties apply to all regular polygons, whether convex or star polygon, star.'' A regular ''n''-sided polygon has rotational symmetry of order ''n''. All vertices of a regular polygon lie on a common circle (the circumscribed circle); i.e., they are concyclic points. That is, a regular polygon is a cyclic polygon. Together with the property of equal-length sides, this implies that every regular p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Directed Edge
In mathematics, and more specifically in graph theory, a directed graph (or digraph) is a graph that is made up of a set of vertices connected by directed edges, often called arcs. Definition In formal terms, a directed graph is an ordered pair where * ''V'' is a set whose elements are called '' vertices'', ''nodes'', or ''points''; * ''A'' is a set of ordered pairs of vertices, called ''arcs'', ''directed edges'' (sometimes simply ''edges'' with the corresponding set named ''E'' instead of ''A''), ''arrows'', or ''directed lines''. It differs from an ordinary or undirected graph, in that the latter is defined in terms of unordered pairs of vertices, which are usually called ''edges'', ''links'' or ''lines''. The aforementioned definition does not allow a directed graph to have multiple arrows with the same source and target nodes, but some authors consider a broader definition that allows directed graphs to have such multiple arcs (namely, they allow the arc set to be a m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex Arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes. For example, a ''square vertex arrangement'' is understood to mean four points in a plane, equal distance and angles from a center point. Two polytopes share the same ''vertex arrangement'' if they share the same 0-skeleton In mathematics, particularly in algebraic topology, the of a topological space presented as a simplicial complex (resp. CW complex) refers to the subspace that is the union of the simplices of (resp. cells of ) of dimensions In other wo .... A group of polytopes that shares a vertex arrangement is called an ''army''. Vertex arrangement The same set of vertices can be connected by edges in different ways. For example, the ''pentagon'' and ''pentagram'' have the same ''vertex arrangement'', while the second connects alternate vertices. A ''vertex arrangement'' is often described by the convex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Star Polygon
In geometry, a star polygon is a type of non-convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, certain notable ones can arise through truncation operations on regular simple and star polygons. Branko Grünbaum identified two primary definitions used by Johannes Kepler, one being the regular star polygons with intersecting edges that don't generate new vertices, and the second being simple isotoxal concave polygons. The first usage is included in polygrams which includes polygons like the pentagram but also compound figures like the hexagram. One definition of a ''star polygon'', used in turtle graphics, is a polygon having 2 or more turns (turning number and density), like in spirolaterals.Abelson, Harold, diSessa, Andera, 1980, ''Turtle Geometry'', MIT Press, p.24 Etymology Star polygon names combine a numeral prefix, such as ''penta-'', with the Greek suffix '' -gram'' (in this cas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
24-gon Rhombic Dissectionx
In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''latus'', meaning "side". It is also called a tetragon, derived from greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons (e.g. pentagon). Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices A, B, C and D is sometimes denoted as \square ABCD. Quadrilaterals are either simple (not self-intersecting), or complex (self-intersecting, or crossed). Simple quadrilaterals are either convex or concave. The interior angles of a simple (and planar) quadrilateral ''ABCD'' add up to 360 degrees of arc, that is :\angle A+\angle B+\angle C+\angle D=360^. This is a special case of the ''n''-gon interior angle sum formula: ''S'' = (''n'' − 2) × 180°. All non-self-crossing quadrilaterals tile the plane, b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
24-gon Rhombic Dissection2
In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''latus'', meaning "side". It is also called a tetragon, derived from greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons (e.g. pentagon). Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices A, B, C and D is sometimes denoted as \square ABCD. Quadrilaterals are either simple (not self-intersecting), or complex (self-intersecting, or crossed). Simple quadrilaterals are either convex or concave. The interior angles of a simple (and planar) quadrilateral ''ABCD'' add up to 360 degrees of arc, that is :\angle A+\angle B+\angle C+\angle D=360^. This is a special case of the ''n''-gon interior angle sum formula: ''S'' = (''n'' − 2) × 180°. All non-self-crossing quadrilaterals tile the plane, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
24-gon Rhombic Dissection
In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''latus'', meaning "side". It is also called a tetragon, derived from greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons (e.g. pentagon). Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices A, B, C and D is sometimes denoted as \square ABCD. Quadrilaterals are either simple (not self-intersecting), or complex (self-intersecting, or crossed). Simple quadrilaterals are either convex or concave. The interior angles of a simple (and planar) quadrilateral ''ABCD'' add up to 360 degrees of arc, that is :\angle A+\angle B+\angle C+\angle D=360^. This is a special case of the ''n''-gon interior angle sum formula: ''S'' = (''n'' − 2) × 180°. All non-self-crossing quadrilaterals tile the plane, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
12-cube
In geometry, a hypercube is an ''n''-dimensional analogue of a square () and a cube (). It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length. A unit hypercube's longest diagonal in ''n'' dimensions is equal to \sqrt. An ''n''-dimensional hypercube is more commonly referred to as an ''n''-cube or sometimes as an ''n''-dimensional cube. The term measure polytope (originally from Elte, 1912) is also used, notably in the work of H. S. M. Coxeter who also labels the hypercubes the γn polytopes. The hypercube is the special case of a hyperrectangle (also called an ''n-orthotope''). A ''unit hypercube'' is a hypercube whose side has length one unit. Often, the hypercube whose corners (or ''vertices'') are the 2''n'' points in R''n'' with each coordinate equal to 0 or 1 is called ''the'' unit hypercube. Construction A hyp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Petrie Polygon
In geometry, a Petrie polygon for a regular polytope of dimensions is a skew polygon in which every consecutive sides (but no ) belongs to one of the facets. The Petrie polygon of a regular polygon is the regular polygon itself; that of a regular polyhedron is a skew polygon such that every two consecutive sides (but no three) belongs to one of the faces. Petrie polygons are named for mathematician John Flinders Petrie. For every regular polytope there exists an orthogonal projection onto a plane such that one Petrie polygon becomes a regular polygon with the remainder of the projection interior to it. The plane in question is the Coxeter plane of the symmetry group of the polygon, and the number of sides, , is the Coxeter number of the Coxeter group. These polygons and projected graphs are useful in visualizing symmetric structure of the higher-dimensional regular polytopes. Petrie polygons can be defined more generally for any embedded graph. They form the faces of anothe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
