|
Inverse Function Rule
In calculus, the inverse function rule is a formula that expresses the derivative of the inverse of a bijective and differentiable function in terms of the derivative of . More precisely, if the inverse of f is denoted as f^, where f^(y) = x if and only if f(x) = y, then the inverse function rule is, in Lagrange's notation, :\left ^\right(y)=\frac. This formula holds in general whenever f is continuous and injective on an interval , with f being differentiable at f^(y)(\in I) and wheref'(f^(y)) \ne 0. The same formula is also equivalent to the expression :\mathcal\left ^\right\frac, where \mathcal denotes the unary derivative operator (on the space of functions) and \circ denotes function composition. Geometrically, a function and inverse function have graphs that are reflections, in the line y=x. This reflection operation turns the gradient of any line into its reciprocal. Assuming that f has an inverse in a neighbourhood of x and that its derivative at that point is non ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiplicative Inverse
In mathematics, a multiplicative inverse or reciprocal for a number ''x'', denoted by 1/''x'' or ''x''−1, is a number which when Multiplication, multiplied by ''x'' yields the multiplicative identity, 1. The multiplicative inverse of a rational number, fraction ''a''/''b'' is ''b''/''a''. For the multiplicative inverse of a real number, divide 1 by the number. For example, the reciprocal of 5 is one fifth (1/5 or 0.2), and the reciprocal of 0.25 is 1 divided by 0.25, or 4. The reciprocal function, the Function (mathematics), function ''f''(''x'') that maps ''x'' to 1/''x'', is one of the simplest examples of a function which is its own inverse (an Involution (mathematics), involution). Multiplying by a number is the same as Division (mathematics), dividing by its reciprocal and vice versa. For example, multiplication by 4/5 (or 0.8) will give the same result as division by 5/4 (or 1.25). Therefore, multiplication by a number followed by multiplication by its reciprocal yie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Functions
In mathematics, the inverse function of a function (also called the inverse of ) is a function that undoes the operation of . The inverse of exists if and only if is bijective, and if it exists, is denoted by f^ . For a function f\colon X\to Y, its inverse f^\colon Y\to X admits an explicit description: it sends each element y\in Y to the unique element x\in X such that . As an example, consider the real-valued function of a real variable given by . One can think of as the function which multiplies its input by 5 then subtracts 7 from the result. To undo this, one adds 7 to the input, then divides the result by 5. Therefore, the inverse of is the function f^\colon \R\to\R defined by f^(y) = \frac . Definitions Let be a function whose domain is the set , and whose codomain is the set . Then is ''invertible'' if there exists a function from to such that g(f(x))=x for all x\in X and f(g(y))=y for all y\in Y. If is invertible, then there is exactly one function ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differentiation Rules
This article is a summary of differentiation rules, that is, rules for computing the derivative of a function (mathematics), function in calculus. Elementary rules of differentiation Unless otherwise stated, all functions are functions of real numbers (\mathbb) that return real values, although, more generally, the formulas below apply wherever they are well defined, including the case of complex numbers (\mathbb). Constant term rule For any value of c, where c \in \mathbb, if f(x) is the constant function given by f(x) = c, then \frac = 0. Proof Let c \in \mathbb and f(x) = c. By the definition of the derivative: \begin f'(x) &= \lim_\frac \\ &= \lim_ \frac \\ &= \lim_ \frac \\ &= \lim_ 0 \\ &= 0. \end This computation shows that the derivative of any constant function is 0. Intuitive (geometric) explanation The derivative of the function at a point is the slope of the line tangent to the curve at the point. The slope of the constant function is 0, because the Tangent, tangen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Articles Containing Proofs
Article often refers to: * Article (grammar), a grammatical element used to indicate definiteness or indefiniteness * Article (publishing), a piece of nonfictional prose that is an independent part of a publication Article(s) may also refer to: Government and law * Elements of treaties of the European Union * Articles of association, the regulations governing a company, used in India, the UK and other countries; called articles of incorporation in the US * Articles of clerkship, the contract accepted to become an articled clerk * Articles of Confederation, the predecessor to the current United States Constitution * Article of impeachment, a formal document and charge used for impeachment in the United States * Article of manufacture, in the United States patent law, a category of things that may be patented * Articles of organization, for limited liability organizations, a US equivalent of articles of association Other uses * Article element , in HTML * "Articles", a song ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Faà Di Bruno's Formula
Faà di Bruno's formula is an identity in mathematics generalizing the chain rule to higher derivatives. It is named after , although he was not the first to state or prove the formula. In 1800, more than 50 years before Faà di Bruno, the French mathematician Louis François Antoine Arbogast had stated the formula in a calculus textbook, which is considered to be the first published reference on the subject. Perhaps the most well-known form of Faà di Bruno's formula says that f(g(x))=\sum \frac\cdot f^(g(x))\cdot \prod_^n\left(g^(x)\right)^, where the sum is over all n-tuples of nonnegative integers (m_1,\ldots,m_n) satisfying the constraint 1\cdot m_1+2\cdot m_2+3\cdot m_3+\cdots+n\cdot m_n=n. Sometimes, to give it a memorable pattern, it is written in a way in which the coefficients that have the combinatorial interpretation discussed below are less explicit: : f(g(x)) =\sum \frac\cdot f^(g(x))\cdot \prod_^n\left(\frac\right)^. Combining the terms with the same value of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Legendre Transformation
In mathematics, the Legendre transformation (or Legendre transform), first introduced by Adrien-Marie Legendre in 1787 when studying the minimal surface problem, is an involutive transformation on real-valued functions that are convex on a real variable. Specifically, if a real-valued multivariable function is convex on one of its independent real variables, then the Legendre transform with respect to this variable is applicable to the function. In physical problems, the Legendre transform is used to convert functions of one quantity (such as position, pressure, or temperature) into functions of the conjugate quantity (momentum, volume, and entropy, respectively). In this way, it is commonly used in classical mechanics to derive the Hamiltonian formalism out of the Lagrangian formalism (or vice versa) and in thermodynamics to derive the thermodynamic potentials, as well as in the solution of differential equations of several variables. For sufficiently smooth functions on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood (or neighborhood) is one of the basic concepts in a topological space. It is closely related to the concepts of open set and Interior (topology), interior. Intuitively speaking, a neighbourhood of a point is a Set (mathematics), set of points containing that point where one can move some amount in any direction away from that point without leaving the set. Definitions Neighbourhood of a point If X is a topological space and p is a point in X, then a neighbourhood of p is a subset V of X that includes an open set U containing p, p \in U \subseteq V \subseteq X. This is equivalent to the point p \in X belonging to the Interior (topology)#Interior point, topological interior of V in X. The neighbourhood V need not be an open subset of X. When V is open (resp. closed, compact, etc.) in X, it is called an (resp. closed neighbourhood, compact neighbourhood, etc.). Some authors require neighbourhoods to be open, so i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral
In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. the other being Derivative, differentiation. Integration was initially used to solve problems in mathematics and physics, such as finding the area under a curve, or determining displacement from velocity. Usage of integration expanded to a wide variety of scientific fields thereafter. A definite integral computes the signed area of the region in the plane that is bounded by the Graph of a function, graph of a given Function (mathematics), function between two points in the real line. Conventionally, areas above the horizontal Coordinate axis, axis of the plane are positive while areas below are n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
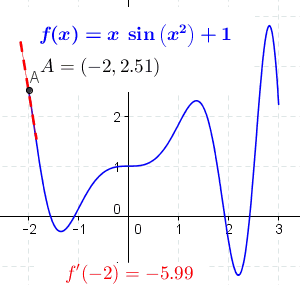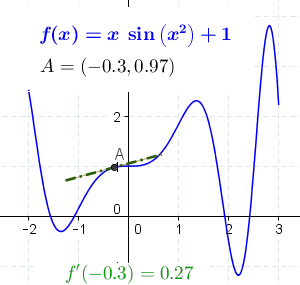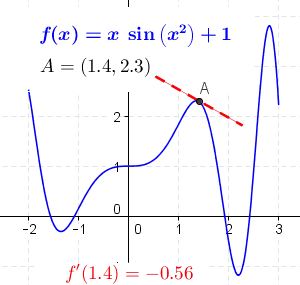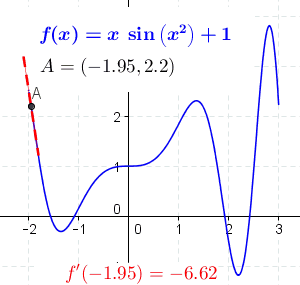
Chain Rule
In calculus, the chain rule is a formula that expresses the derivative of the Function composition, composition of two differentiable functions and in terms of the derivatives of and . More precisely, if h=f\circ g is the function such that h(x)=f(g(x)) for every , then the chain rule is, in Lagrange's notation, h'(x) = f'(g(x)) g'(x). or, equivalently, h'=(f\circ g)'=(f'\circ g)\cdot g'. The chain rule may also be expressed in Leibniz's notation. If a variable depends on the variable , which itself depends on the variable (that is, and are dependent variables), then depends on as well, via the intermediate variable . In this case, the chain rule is expressed as \frac = \frac \cdot \frac, and \left.\frac\_ = \left.\frac\_ \cdot \left. \frac\_ , for indicating at which points the derivatives have to be evaluated. In integral, integration, the counterpart to the chain rule is the substitution rule. Intuitive explanation Intuitively, the chain rule states that knowing t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leibniz's Notation
In calculus, Leibniz's notation, named in honor of the 17th-century German philosopher and mathematician Gottfried Wilhelm Leibniz, uses the symbols and to represent infinitely small (or infinitesimal) increments of and , respectively, just as and represent finite increments of and , respectively. Consider as a function of a variable , or = . If this is the case, then the derivative of with respect to , which later came to be viewed as the limit :\lim_\frac = \lim_\frac, was, according to Leibniz, the quotient of an infinitesimal increment of by an infinitesimal increment of , or :\frac=f'(x), where the right hand side is Joseph-Louis Lagrange's notation for the derivative of at . The infinitesimal increments are called . Related to this is the integral in which the infinitesimal increments are summed (e.g. to compute lengths, areas and volumes as sums of tiny pieces), for which Leibniz also supplied a closely related notation involving the same differentials ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neighborhood (mathematics)
In topology and related areas of mathematics, a neighbourhood (or neighborhood) is one of the basic concepts in a topological space. It is closely related to the concepts of open set and interior. Intuitively speaking, a neighbourhood of a point is a set of points containing that point where one can move some amount in any direction away from that point without leaving the set. Definitions Neighbourhood of a point If X is a topological space and p is a point in X, then a neighbourhood of p is a subset V of X that includes an open set U containing p, p \in U \subseteq V \subseteq X. This is equivalent to the point p \in X belonging to the topological interior of V in X. The neighbourhood V need not be an open subset of X. When V is open (resp. closed, compact, etc.) in X, it is called an (resp. closed neighbourhood, compact neighbourhood, etc.). Some authors require neighbourhoods to be open, so it is important to note their conventions. A set that is a neighbourhood ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |