|
Interest Rate Cap And Floor
In finance, an interest rate cap is a type of interest rate derivative in which the buyer receives payments at the end of each period in which the interest rate exceeds the agreed strike price. An example of a cap would be an agreement to receive a payment for each month the LIBOR rate exceeds 2.5%. Similarly, an interest rate floor is a derivative contract in which the buyer receives payments at the end of each period in which the interest rate is below the agreed strike price. Caps and floors can be used to hedge against interest rate fluctuations. For example, a borrower who is paying the LIBOR rate on a loan can protect himself against a rise in rates by buying a cap at 2.5%. If the interest rate exceeds 2.5% in a given period the payment received from the derivative can be used to help make the interest payment for that period, thus the interest payments are effectively "capped" at 2.5% from the borrowers' point of view. Interest rate cap An interest rate cap is a deri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finance
Finance refers to monetary resources and to the study and Academic discipline, discipline of money, currency, assets and Liability (financial accounting), liabilities. As a subject of study, is a field of Business administration, Business Administration wich study the planning, organizing, leading, and controlling of an organization's resources to achieve its goals. Based on the scope of financial activities in financial systems, the discipline can be divided into Personal finance, personal, Corporate finance, corporate, and public finance. In these financial systems, assets are bought, sold, or traded as financial instruments, such as Currency, currencies, loans, Bond (finance), bonds, Share (finance), shares, stocks, Option (finance), options, Futures contract, futures, etc. Assets can also be banked, Investment, invested, and Insurance, insured to maximize value and minimize loss. In practice, Financial risk, risks are always present in any financial action and entities. Due ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Log-normal Distribution
In probability theory, a log-normal (or lognormal) distribution is a continuous probability distribution of a random variable whose logarithm is normal distribution, normally distributed. Thus, if the random variable is log-normally distributed, then has a normal distribution. Equivalently, if has a normal distribution, then the exponential function of , , has a log-normal distribution. A random variable which is log-normally distributed takes only positive real values. It is a convenient and useful model for measurements in exact and engineering sciences, as well as medicine, economics and other topics (e.g., energies, concentrations, lengths, prices of financial instruments, and other metrics). The distribution is occasionally referred to as the Galton distribution or Galton's distribution, after Francis Galton. The log-normal distribution has also been associated with other names, such as Donald MacAlister#log-normal, McAlister, Gibrat's law, Gibrat and Cobb–Douglas. A l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
University Of Basel
The University of Basel (Latin: ''Universitas Basiliensis''; German: ''Universität Basel'') is a public research university in Basel, Switzerland. Founded on 4 April 1460, it is Switzerland's oldest university and among the world's oldest universities. The university is traditionally counted among the leading institutions of higher learning in the country. The associated Basel University Library is the largest and among the most important libraries in Switzerland. The university hosts the faculties of theology, law, medicine, humanities and social sciences, science, psychology, and business and economics, as well as numerous cross-disciplinary subjects and institutes, such as the Biozentrum for biomedical research and the Institute for European Global Studies. In 2020, the university had 13,139 students and 378 professors. International students accounted for 27 percent of the student body. In its over 500-year history, the university has been home to Erasmus of Rotterdam, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Wiley & Sons
John Wiley & Sons, Inc., commonly known as Wiley (), is an American Multinational corporation, multinational Publishing, publishing company that focuses on academic publishing and instructional materials. The company was founded in 1807 and produces books, Academic journal, journals, and encyclopedias, in print and electronically, as well as online products and services, training materials, and educational materials for undergraduate, graduate, and continuing education students. History The company was established in 1807 when Charles Wiley opened a print shop in Manhattan. The company was the publisher of 19th century American literary figures like James Fenimore Cooper, Washington Irving, Herman Melville, and Edgar Allan Poe, as well as of legal, religious, and other non-fiction titles. The firm took its current name in 1865. Wiley later shifted its focus to scientific, Technology, technical, and engineering subject areas, abandoning its literary interests. Wiley's son Joh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
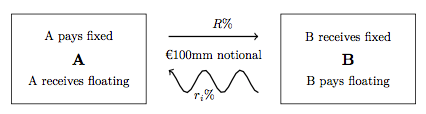
Interest Rate Swap
In finance, an interest rate swap (IRS) is an interest rate derivative (IRD). It involves exchange of interest rates between two parties. In particular it is a "linear" IRD and one of the most liquid, benchmark products. It has associations with forward rate agreements (FRAs), and with zero coupon swaps (ZCSs). In its December 2014 statistics release, the Bank for International Settlements reported that interest rate swaps were the largest component of the global OTC derivative market, representing 60%, with the notional amount outstanding in OTC interest rate swaps of $381 trillion, and the gross market value of $14 trillion. Interest rate swaps can be traded as an index through the FTSE MTIRS Index. Interest rate swaps General description An interest rate swap's (IRS's) effective description is a derivative contract, agreed between two counterparties, which specifies the nature of an exchange of payments benchmarked against an interest rate index. The most common IRS ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Put–call Parity
In financial mathematics, the put–call parity defines a relationship between the price of a European call option and European put option, both with the identical strike price and expiry, namely that a portfolio of a long call option and a short put option is equivalent to (and hence has the same value as) a single forward contract at this strike price and expiry. This is because if the price at expiry is above the strike price, the call will be exercised, while if it is below, the put will be exercised, and thus in either case one unit of the asset will be purchased for the strike price, exactly as in a forward contract. The validity of this relationship requires that certain assumptions be satisfied; these are specified and the relationship is derived below. In practice transaction costs and financing costs (leverage) mean this relationship will not exactly hold, but in liquid markets the relationship is close to exact. Assumptions Put–call parity is a static replication, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hull–White Model
In financial mathematics, the Hull–White model is a model of future interest rates. In its most generic formulation, it belongs to the class of no-arbitrage models that are able to fit today's term structure of interest rates. It is relatively straightforward to translate the mathematical description of the evolution of future interest rates onto a tree or lattice and so interest rate derivatives such as bermudan swaptions can be valued in the model. The first Hull–White model was described by John C. Hull and Alan White in 1990. The model is still popular in the market today. The model One-factor model The model is a short-rate model. In general, it has the following dynamics: :dr(t) = \left theta(t) - \alpha(t) r(t)\right,dt + \sigma(t)\, dW(t). There is a degree of ambiguity among practitioners about exactly which parameters in the model are time-dependent or what name to apply to the model in each case. The most commonly accepted naming convention is the following: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Short-rate Model
A short-rate model, in the context of interest rate derivatives, is a mathematical model that describes the future evolution of interest rates by describing the future evolution of the short rate, usually written r_t \,. The short rate Under a short rate model, the stochastic state variable is taken to be the instantaneous spot rate. The short rate, r_t \,, then, is the (Compound interest#Continuous compounding, continuously compounded, annualized) interest rate at which an entity can borrow money for an infinitesimally short period of time from time t. Specifying the current short rate does not specify the entire yield curve. However, arbitrage, no-arbitrage arguments show that, under some fairly relaxed technical conditions, if we model the evolution of r_t \, as a stochastic process under a risk-neutral measure Q, then the price at time t of a zero-coupon bond maturing at time T with a payoff of 1 is given by : P(t,T) = \operatorname^Q\left[\left. \exp \ \mathcal_t \right], w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantitative Easing
Quantitative easing (QE) is a monetary policy action where a central bank purchases predetermined amounts of government bonds or other financial assets in order to stimulate economic activity. Quantitative easing is a novel form of monetary policy that came into wide application following the 2008 financial crisis. It is used to mitigate an economic recession when inflation is very low or negative, making standard monetary policy ineffective. Quantitative tightening (QT) does the opposite, where for monetary policy reasons, a central bank sells off some portion of its holdings of government bonds or other financial assets. Similar to conventional Open market operation, open-market operations used to implement monetary policy, a central bank implements quantitative easing by buying financial assets from commercial banks and other financial institutions, thus raising the prices of those financial assets and lowering their Yield (finance), yield, while simultaneously increasing the m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Forward Price
The forward price (or sometimes forward rate) is the agreed upon price of an asset in a forward contract. Using the rational pricing assumption, for a forward contract on an underlying asset that is tradeable, the forward price can be expressed in terms of the spot price and any dividends. For forwards on non-tradeables, pricing the forward may be a complex task. Forward price formula If the underlying asset is tradable and a dividend exists, the forward price is given by: : F = S_0 e^ - \sum_^N D_i e^ \, where :F is the forward price to be paid at time T :e^x is the exponential function (used for calculating continuous compounding interests) :r is the risk-free interest rate :q is the convenience yield :S_0 is the spot price of the asset (i.e. what it would sell for at time 0) :D_i is a dividend that is guaranteed to be paid at time t_i where 0< t_i < T. Proof of the forward price formula The two questions here are what price the short position ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
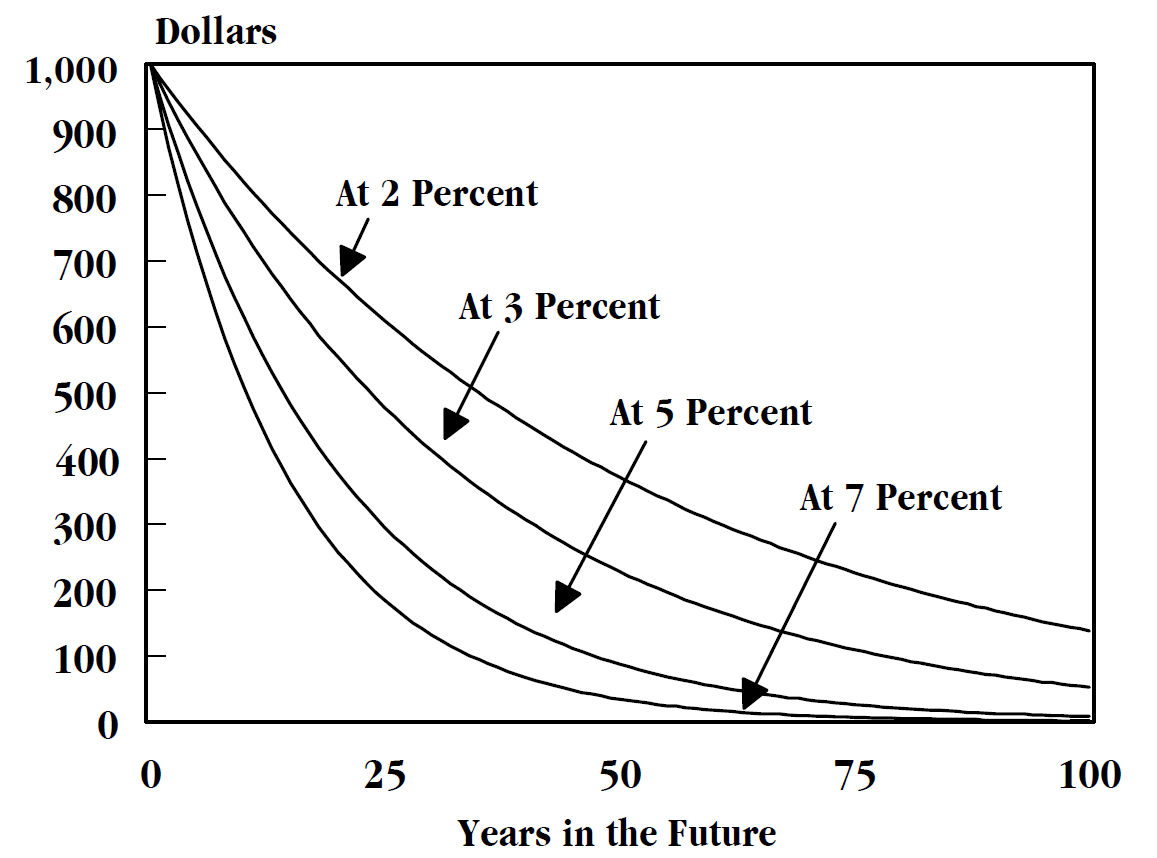
Discount Factor
In finance, discounting is a mechanism in which a debtor obtains the right to delay payments to a creditor, for a defined period of time, in exchange for a charge or fee.See "Time Value", "Discount", "Discount Yield", "Compound Interest", "Efficient Market", "Market Value" and "Opportunity Cost" in Downes, J. and Goodman, J. E. ''Dictionary of Finance and Investment Terms'', Baron's Financial Guides, 2003. Essentially, the party that owes money in the present purchases the right to delay the payment until some future date.See "Discount", "Compound Interest", "Efficient Markets Hypothesis", "Efficient Resource Allocation", "Pareto-Optimality", "Price", "Price Mechanism" and "Efficient Market" in Black, John, ''Oxford Dictionary of Economics'', Oxford University Press, 2002. This transaction is based on the fact that most people prefer current interest to delayed interest because of mortality effects, impatience effects, and salience effects. The discount, or charge, is the dif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |