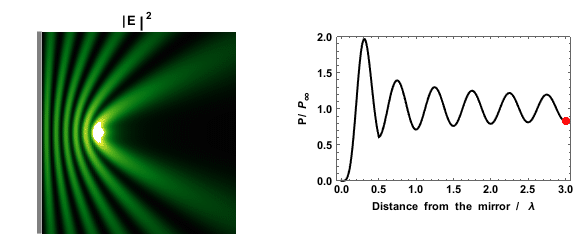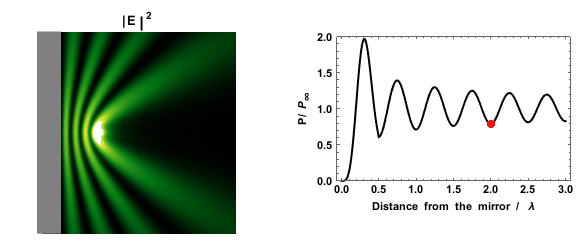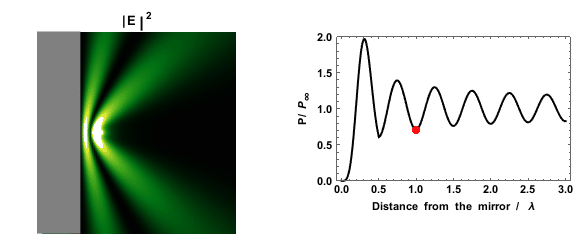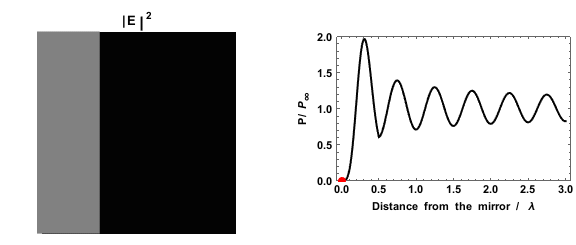
|
Interaction Picture
In quantum mechanics, the interaction picture (also known as the interaction representation or Dirac picture after Paul Dirac, who introduced it) is an intermediate representation between the Schrödinger picture and the Heisenberg picture. Whereas in the other two pictures either the state vector or the operators carry time dependence, in the interaction picture both carry part of the time dependence of observables. The interaction picture is useful in dealing with changes to the wave functions and observables due to interactions. Most field-theoretical calculations use the interaction representation because they construct the solution to the many-body Schrödinger equation as the solution to free particles in presence of some unknown interacting parts. Equations that include operators acting at different times, which hold in the interaction picture, don't necessarily hold in the Schrödinger or the Heisenberg picture. This is because time-dependent unitary transformations r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science. Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and Microscopic scale, (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Classical mechanics can be derived from quantum mechanics as an approximation that is valid at ordinary scales. Quantum systems have Bound state, bound states that are Quantization (physics), quantized to Discrete mathematics, discrete values of energy, momentum, angular momentum, and ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Field
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines field theory and the principle of relativity with ideas behind quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles and in condensed matter physics to construct models of quasiparticles. The current standard model of particle physics is based on QFT. History Quantum field theory emerged from the work of generations of theoretical physicists spanning much of the 20th century. Its development began in the 1920s with the description of interactions between light and electrons, culminating in the first quantum field theory—quantum electrodynamics. A major theoretical obstacle soon followed with the appearance and persistence of various infinities in perturbative calculations, a problem only resolved in the 1950s with the invention of the renormalization procedure. A second major barrier came with QFT's apparent inability to describe the wea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bra–ket Notation
Bra–ket notation, also called Dirac notation, is a notation for linear algebra and linear operators on complex vector spaces together with their dual space both in the finite-dimensional and infinite-dimensional case. It is specifically designed to ease the types of calculations that frequently come up in quantum mechanics. Its use in quantum mechanics is quite widespread. Bra–ket notation was created by Paul Dirac in his 1939 publication ''A New Notation for Quantum Mechanics''. The notation was introduced as an easier way to write quantum mechanical expressions. The name comes from the English word "bracket". Quantum mechanics In quantum mechanics and quantum computing, bra–ket notation is used ubiquitously to denote quantum states. The notation uses angle brackets, and , and a vertical bar , to construct "bras" and "kets". A ket is of the form , v \rangle. Mathematically it denotes a vector, \boldsymbol v, in an abstract (complex) vector space V, and physicall ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pergamon Press
Pergamon Press was an Oxford-based publishing house, founded by Paul Rosbaud and Robert Maxwell, that published scientific and medical books and journals. Originally called Butterworth-Springer, it is now an imprint of Elsevier. History The core company, Butterworth-Springer, started in 1948 to bring the "Springer know-how and techniques of aggressive publishing in science"Joe Haines (1988) ''Maxwell'', Houghton Mifflin, p. 137. to Britain. Paul Rosbaud was the man with the knowledge. When Maxwell acquired the company in 1951, Rosbaud held a one-quarter share. They changed the house name to Pergamon Press, using a logo that was a reproduction of a Greek coin from Pergamon. Maxwell and Rosbaud worked together growing the company until May 1956, when, according to Joe Haines, Rosbaud was sacked. When Pergamon Press started it had only six serials and two books. Initially the company headquarters was in Fitzroy Square in West End of London. In 1959, the company moved into He ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Field Operators
In physics, canonical quantization is a procedure for quantizing a classical theory, while attempting to preserve the formal structure, such as symmetries, of the classical theory to the greatest extent possible. Historically, this was not quite Werner Heisenberg's route to obtaining quantum mechanics, but Paul Dirac introduced it in his 1926 doctoral thesis, the "method of classical analogy" for quantization, and detailed it in his classic text ''Principles of Quantum Mechanics''. The word ''canonical'' arises from the Hamiltonian approach to classical mechanics, in which a system's dynamics is generated via canonical Poisson brackets, a structure which is ''only partially preserved'' in canonical quantization. This method was further used by Paul Dirac in the context of quantum field theory, in his construction of quantum electrodynamics. In the field theory context, it is also called the second quantization of fields, in contrast to the semi-classical first quantization of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Julian Schwinger
Julian Seymour Schwinger (; February 12, 1918 – July 16, 1994) was a Nobel Prize-winning American theoretical physicist. He is best known for his work on quantum electrodynamics (QED), in particular for developing a relativistically invariant perturbation theory, and for renormalizing QED to one loop order. Schwinger was a physics professor at several universities. Schwinger is recognized as an important physicist, responsible for much of modern quantum field theory, including a variational approach, and the equations of motion for quantum fields. He developed the first electroweak model, and the first example of confinement in 1+1 dimensions. He is responsible for the theory of multiple neutrinos, Schwinger terms, and the theory of the spin-3/2 field. Biography Early life and career Julian Seymour Schwinger was born in New York City, to Ashkenazi Jewish parents, Belle (née Rosenfeld) and Benjamin Schwinger, a garment manufacturer, who had emigrated from Poland to the Unite ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shin'ichirō Tomonaga
, usually cited as Sin-Itiro Tomonaga in English, was a Japanese physicist, influential in the development of quantum electrodynamics, work for which he was jointly awarded the Nobel Prize in Physics in 1965 along with Richard Feynman and Julian Schwinger. Biography Tomonaga was born in Tokyo in 1906. He was the second child and eldest son of a Japanese philosopher, Tomonaga Sanjūrō. He entered the Kyoto Imperial University in 1926. Hideki Yukawa, also a Nobel laureate, was one of his classmates during undergraduate school. During graduate school at the same university, he worked as an assistant in the university for three years. In 1931, after graduate school, he joined Nishina's group in RIKEN. In 1937, while working at Leipzig University (Leipzig), he collaborated with the research group of Werner Heisenberg. Two years later, he returned to Japan due to the outbreak of the Second World War, but finished his doctoral degree (Dissertation PhD from University of Tokyo) on the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Field Theory
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines Field theory (physics), field theory and the principle of relativity with ideas behind quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles and in condensed matter physics to construct models of quasiparticles. The current standard model of particle physics is based on QFT. History Quantum field theory emerged from the work of generations of theoretical physicists spanning much of the 20th century. Its development began in the 1920s with the description of interactions between light and electrons, culminating in the first quantum field theory—quantum electrodynamics. A major theoretical obstacle soon followed with the appearance and persistence of various infinities in perturbative calculations, a problem only resolved in the 1950s with the invention of the renormalization procedure. A second major barrier came with QFT's apparent inabili ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dyson Series
In scattering theory, a part of mathematical physics, the Dyson series, formulated by Freeman Dyson, is a perturbative expansion of the time evolution operator in the interaction picture. Each term can be represented by a sum of Feynman diagrams. This series diverges asymptotically, but in quantum electrodynamics (QED) at the second order the difference from experimental data is in the order of 10−10. This close agreement holds because the coupling constant (also known as the fine-structure constant) of QED is much less than 1. Dyson operator In the interaction picture, a Hamiltonian , can be split into a ''free'' part and an ''interacting part'' as . The potential in the interacting picture is :V_(t) = \mathrm^ V_(t) \mathrm^, where H_0 is time-independent and V_(t) is the possibly time-dependent interacting part of the Schrödinger picture. To avoid subscripts, V(t) stands for V_\mathrm(t) in what follows. In the interaction picture, the evolution oper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermi's Golden Rule
In quantum physics, Fermi's golden rule is a formula that describes the transition rate (the probability of a transition per unit time) from one energy eigenstate of a quantum system to a group of energy eigenstates in a continuum, as a result of a weak Perturbation theory (quantum mechanics), perturbation. This transition rate is effectively independent of time (so long as the strength of the perturbation is independent of time) and is proportional to the strength of the coupling between the initial and final states of the system (described by the square of the Matrix element (physics), matrix element of the perturbation) as well as the density of states. It is also applicable when the final state is discrete, i.e. it is not part of a continuum, if there is some decoherence in the process, like relaxation or collision of the atoms, or like noise in the perturbation, in which case the density of states is replaced by the reciprocal of the decoherence bandwidth. Historical background ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perturbation Theory (quantum Mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an additional "perturbing" Hamiltonian representing a weak disturbance to the system. If the disturbance is not too large, the various physical quantities associated with the perturbed system (e.g. its energy levels and eigenstates) can be expressed as "corrections" to those of the simple system. These corrections, being small compared to the size of the quantities themselves, can be calculated using approximate methods such as asymptotic series. The complicated system can therefore be studied based on knowledge of the simpler one. In effect, it is describing a complicated unsolved system using a simple, solvable system. Approximate Hamiltonians Perturbation theory is an important tool for de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density Matrix
In quantum mechanics, a density matrix (or density operator) is a matrix used in calculating the probabilities of the outcomes of measurements performed on physical systems. It is a generalization of the state vectors or wavefunctions: while those can only represent pure states, density matrices can also represent mixed states. These arise in quantum mechanics in two different situations: # when the preparation of a system can randomly produce different pure states, and thus one must deal with the statistics of possible preparations, and # when one wants to describe a physical system that is entangled with another, without describing their combined state. This case is typical for a system interacting with some environment (e.g. decoherence). In this case, the density matrix of an entangled system differs from that of an ensemble of pure states that, combined, would give the same statistical results upon measurement. Density matrices are thus crucial tools in areas of quantum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |