|
Independence Of Smith-dominated Alternatives
Independence of Smith-dominated alternatives (ISDA, also known as Smith-IIA or Weak independence of irrelevant alternatives) is a voting system criterion defined such that its satisfaction by a voting system occurs when the selection of the winner is independent of candidates who are not within the Smith set. A simple way to describe it is that if a voting system is ISDA, then whenever you can partition the candidates into group ''A'' and group ''B'' such that each candidate in group ''A'' is preferred over each candidate in group ''B'', you can eliminate all candidates of group ''B'' without changing the outcome of the election. Any election method that is independent of Smith-dominated alternatives automatically satisfies the Smith criterion (because all candidates not in the Smith set can be eliminated without changing the result, implying that the winner was someone in the Smith set), and all criteria implied by it, notably the Condorcet criterion and the mutual majority crit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Independence Of Irrelevant Alternatives
The independence of irrelevant alternatives (IIA), also known as binary independence or the independence axiom, is an axiom of decision theory and various social sciences. The term is used in different connotation in several contexts. Although it always attempts to provide an account of rational individual behavior or aggregation of individual preferences, the exact formulation differs widely in both language and exact content. Perhaps the easiest way to understand the axiom is how it pertains to casting a ballot. There the axiom says that if Charlie (the irrelevant alternative) enters a race between Alice and Bob, with Alice (leader) liked better than Bob (runner-up), then the individual voter who likes Charlie less than Alice will not switch his vote from Alice to Bob. Because of this, a violation of IIA is commonly referred to as the "spoiler effect": support for Charlie "spoils" the election for Alice, while it "logically" should not have. After all, Alice ''was'' liked better t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Voting System Criterion
Electoral systems are the rules for conducting elections, a main component of which is the algorithm for determining the winner (or several winners) from the ballots cast. This article discusses methods and results of comparing different electoral systems, both those which elect a unique candidate in a 'single-winner' election and those which elect a group of representatives in a multiwinner election. There are 4 main types of reasoning which have been used to try to determine the best voting method: # Argument by example # Adherence to logical criteria # Results of simulated elections # Results of real elections Expert opinions on single-winner voting methods In 2010, a panel of 22 experts on voting procedures were asked: "What is the best voting rule for your town to use to elect the mayor?". One member abstained. Approval voting was used to decide between 18 single-winner voting methods. The ranking (with number ''N'' of approvers from a maximum of 21) of the various syst ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
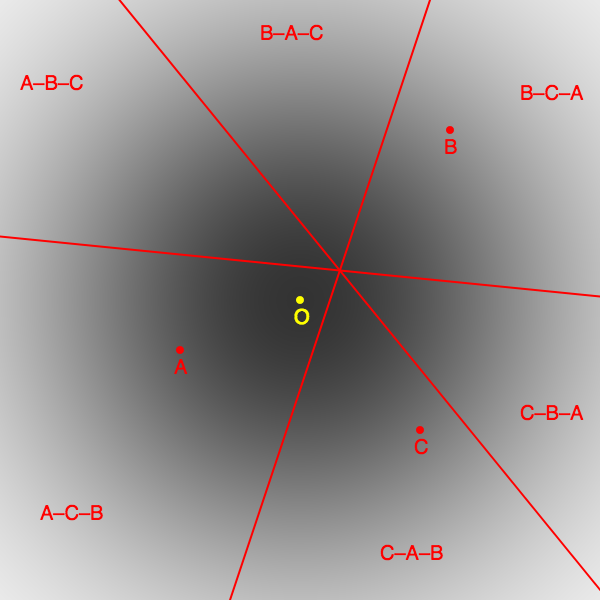
Smith Set
In voting systems, the Smith set, named after John H. Smith, but also known as the top cycle, or as Generalized Top-Choice Assumption (GETCHA), is the smallest non-empty set of candidates in a particular election such that each member defeats every candidate outside the set in a pairwise election. The Smith set provides one standard of optimal choice for an election outcome. Voting systems that always elect a candidate from the Smith set pass the Smith criterion and are said to be 'Smith-efficient' or to satisfy the Smith criterion. A set of candidates each of whose members pairwise defeats every candidate outside the set is known as a dominating set. The Smith set can be seen as defining a voting method (Smith's method) which is most often encountered when extended by an IRV tie-break as Smith/IRV or as Tideman's Alternative, or by minimax as Smith/minimax. Properties of Smith sets *The Smith set always exists and is well defined (see next section). *The Smith set can have mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Smith Criterion
The Smith criterion (sometimes generalized Condorcet criterion, but this can have other meanings) is a voting systems criterion defined such that it's satisfied when a voting system always elects a candidate that is in the Smith set, which is the smallest non-empty subset of the candidates such that every candidate in the subset is majority-preferred over every candidate not in the subset. (A candidate X is said to be majority-preferred over another candidate Y if, in a one-on-one competition between X & Y, the number of voters who prefer X over Y exceeds the number of voters who prefer Y over X.) The Smith set is named for mathematician John H Smith, whose version of the Condorcet criterion is actually stronger than that defined above for social welfare functions. Benjamin Ward was probably the first to write about this set, which he called the "majority set". The Smith set is also called the ''top cycle''. The term ''top cycle'' may be somewhat misleading, however, since the S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Condorcet Criterion
An electoral system satisfies the Condorcet winner criterion () if it always chooses the Condorcet winner when one exists. The candidate who wins a majority of the vote in every head-to-head election against each of the other candidatesthat is, a candidate preferred by more voters than any othersis the Condorcet winner, although Condorcet winners do not exist in all cases. It is sometimes simply referred to as the "Condorcet criterion", though it is very different from the "Condorcet loser criterion". Any voting method conforming to the Condorcet winner criterion is known as a Condorcet method. The Condorcet winner is the person who would win a two-candidate election against each of the other candidates in a plurality vote. For a set of candidates, the Condorcet winner is always the same regardless of the voting system in question, and can be discovered by using pairwise counting on voters' ranked preferences. A Condorcet winner will not always exist in a given set of votes, which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mutual Majority Criterion
The mutual majority criterion is a criterion used to compare voting systems. It is also known as the majority criterion for solid coalitions and the generalized majority criterion. The criterion states that if there is a subset S of the candidates, such that more than half of the voters strictly prefer every member of S to every candidate outside of S, this majority voting sincerely, the winner must come from S. This is similar to but stricter than the majority criterion, where the requirement applies only to the case that ''S'' contains a single candidate. This is also stricter than the majority loser criterion, where the requirement applies only to the case that ''S'' contains all but one candidate. The mutual majority criterion is the single-winner case of the Droop proportionality criterion. The Schulze method, ranked pairs, instant-runoff voting, Nanson's method, and Bucklin voting pass this criterion. All Smith-efficient Condorcet methods pass the mutual majority criterion ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Independence Of Irrelevant Alternatives
The independence of irrelevant alternatives (IIA), also known as binary independence or the independence axiom, is an axiom of decision theory and various social sciences. The term is used in different connotation in several contexts. Although it always attempts to provide an account of rational individual behavior or aggregation of individual preferences, the exact formulation differs widely in both language and exact content. Perhaps the easiest way to understand the axiom is how it pertains to casting a ballot. There the axiom says that if Charlie (the irrelevant alternative) enters a race between Alice and Bob, with Alice (leader) liked better than Bob (runner-up), then the individual voter who likes Charlie less than Alice will not switch his vote from Alice to Bob. Because of this, a violation of IIA is commonly referred to as the "spoiler effect": support for Charlie "spoils" the election for Alice, while it "logically" should not have. After all, Alice ''was'' liked better t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Independence Of Irrelevant Alternatives
The independence of irrelevant alternatives (IIA), also known as binary independence or the independence axiom, is an axiom of decision theory and various social sciences. The term is used in different connotation in several contexts. Although it always attempts to provide an account of rational individual behavior or aggregation of individual preferences, the exact formulation differs widely in both language and exact content. Perhaps the easiest way to understand the axiom is how it pertains to casting a ballot. There the axiom says that if Charlie (the irrelevant alternative) enters a race between Alice and Bob, with Alice (leader) liked better than Bob (runner-up), then the individual voter who likes Charlie less than Alice will not switch his vote from Alice to Bob. Because of this, a violation of IIA is commonly referred to as the "spoiler effect": support for Charlie "spoils" the election for Alice, while it "logically" should not have. After all, Alice ''was'' liked better t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Condorcet Winner
An electoral system satisfies the Condorcet winner criterion () if it always chooses the Condorcet winner when one exists. The candidate who wins a majority of the vote in every head-to-head election against each of the other candidatesthat is, a candidate preferred by more voters than any othersis the Condorcet winner, although Condorcet winners do not exist in all cases. It is sometimes simply referred to as the "Condorcet criterion", though it is very different from the "Condorcet loser criterion". Any voting method conforming to the Condorcet winner criterion is known as a Condorcet method. The Condorcet winner is the person who would win a two-candidate election against each of the other candidates in a plurality vote. For a set of candidates, the Condorcet winner is always the same regardless of the voting system in question, and can be discovered by using pairwise counting on voters' ranked preferences. A Condorcet winner will not always exist in a given set of votes, which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schulze Method
The Schulze method () is an electoral system developed in 1997 by Markus Schulze that selects a single winner using votes that express preferences. The method can also be used to create a sorted list of winners. The Schulze method is also known as Schwartz Sequential dropping (SSD), cloneproof Schwartz sequential dropping (CSSD), the beatpath method, beatpath winner, path voting, and path winner. The Schulze method is a Condorcet method, which means that if there is a candidate who is preferred by a majority over every other candidate in pairwise comparisons, then this candidate will be the winner when the Schulze method is applied. The output of the Schulze method gives an ordering of candidates. Therefore, if several positions are available, the method can be used for this purpose without modification, by letting the ''k'' top-ranked candidates win the ''k'' available seats. Furthermore, for proportional representation elections, a single transferable vote (STV) variant known as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ranked Pairs
Ranked pairs (sometimes abbreviated "RP") or the Tideman method is an electoral system developed in 1987 by Nicolaus Tideman that selects a single winner using votes that express preferences. The ranked-pairs procedure can also be used to create a sorted list of winners. If there is a candidate who is preferred over the other candidates, when compared in turn with each of the others, the ranked-pairs procedure guarantees that candidate will win. Because of this property, the ranked-pairs procedure complies with the Condorcet winner criterion (and is a Condorcet method). Procedure The ranked-pairs procedure operates as follows: # Tally the vote count comparing each pair of candidates, and determine the winner of each pair (provided there is not a tie) # Sort (rank) each pair, by strength of victory, from largest first to smallest last.In fact, there are different ways how the ''strength of a victory'' is measured. This article uses Tideman's original method based on margins of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |