|
Hit-or-miss Transform
In mathematical morphology, hit-or-miss transform is an operation that detects a given configuration (or pattern) in a binary image, using the morphological erosion (morphology), erosion operator and a pair of Disjoint sets, disjoint structuring elements. The result of the hit-or-miss transform is the set of positions where the first structuring element fits in the foreground of the input image, and the second structuring element misses it completely. Mathematical definition In binary morphology, an image is viewed as a subset of a Euclidean space \mathbb^d or the integer grid \mathbb^d, for some dimension ''d''. Let us denote this space or grid by ''E''. A structuring element is a simple, pre-defined shape, represented as a binary image, used to probe another binary image, in morphological operations such as erosion (morphology), erosion, dilation (morphology), dilation, opening (morphology), opening, and closing (morphology), closing. Let C and D be two structuring elements ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Structure One
A structure is an arrangement and organization of interrelated elements in a material object or system, or the object or system so organized. Material structures include man-made objects such as buildings and machines and natural objects such as biological organisms, minerals and chemicals. Abstract structures include data structures in computer science and musical form. Types of structure include a hierarchy (a cascade of one-to-many relationships), a network featuring many-to-many links, or a lattice featuring connections between components that are neighbors in space. Load-bearing Buildings, aircraft, skeletons, anthills, beaver dams, bridges and salt domes are all examples of load-bearing structures. The results of construction are divided into buildings and non-building structures, and make up the infrastructure of a human society. Built structures are broadly divided by their varying design approaches and standards, into categories including building structures, archi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Euler Number (topology)
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic (or Euler number, or Euler–Poincaré characteristic) is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent. It is commonly denoted by \chi ( Greek lower-case letter chi). The Euler characteristic was originally defined for polyhedra and used to prove various theorems about them, including the classification of the Platonic solids. It was stated for Platonic solids in 1537 in an unpublished manuscript by Francesco Maurolico. Leonhard Euler, for whom the concept is named, introduced it for convex polyhedra more generally but failed to rigorously prove that it is an invariant. In modern mathematics, the Euler characteristic arises from homology and, more abstractly, homological algebra. Polyhedra The Euler characteristic was classically defined for the surfaces of polyhedra, according to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
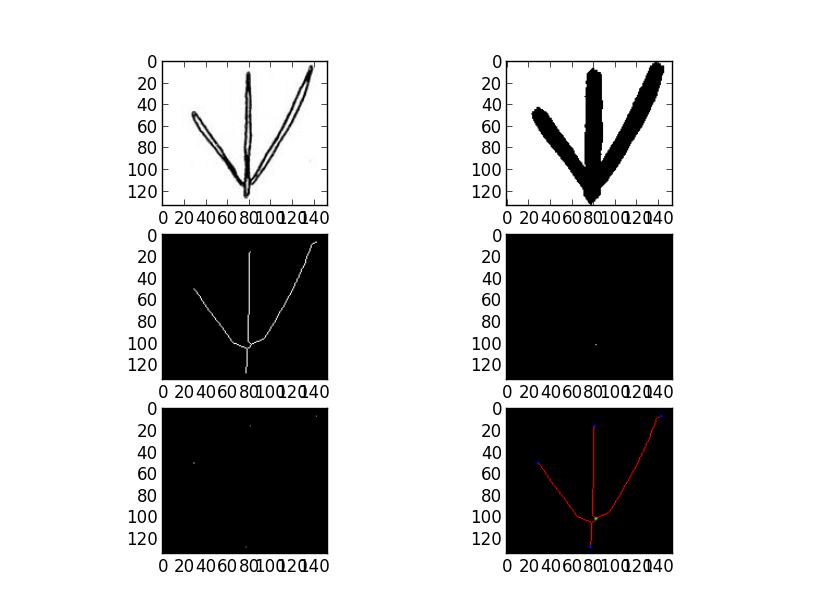
Pruning (morphology)
The pruning algorithm is a technique used in digital image processing based on mathematical morphology. It is used as a complement to the skeleton and thinning algorithms to remove unwanted parasitic components (spurs). In this case 'parasitic' components refer to branches of a line which are not key to the overall shape of the line and should be removed. These components can often be created by edge detection algorithms or digitization. Common uses for pruning include automatic recognition of hand-printed characters. Often inconsistency in letter writing creates unwanted spurs that need to be eliminated for better characterization. Mathematical Definition The standard pruning algorithm will remove all branches shorter than a given number of points. If a parasitic branch is shorter than four points and we run the algorithm with ''n = 4'' the branch will be removed. The second step ensures that the main trunks of each line are not shortened by the procedure. Structuring Element ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Pattern Detection
Pattern recognition is the task of assigning a class to an observation based on patterns extracted from data. While similar, pattern recognition (PR) is not to be confused with pattern machines (PM) which may possess PR capabilities but their primary function is to distinguish and create emergent patterns. PR has applications in statistical data analysis, signal processing, image analysis, information retrieval, bioinformatics, data compression, computer graphics and machine learning. Pattern recognition has its origins in statistics and engineering; some modern approaches to pattern recognition include the use of machine learning, due to the increased availability of big data and a new abundance of processing power. Pattern recognition systems are commonly trained from labeled "training" data. When no labeled data are available, other algorithms can be used to discover previously unknown patterns. KDD and data mining have a larger focus on unsupervised methods and stronger c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Set Minus
In set theory, the complement of a set , often denoted by A^c (or ), is the set of elements not in . When all elements in the universe, i.e. all elements under consideration, are considered to be members of a given set , the absolute complement of is the set of elements in that are not in . The relative complement of with respect to a set , also termed the set difference of and , written B \setminus A, is the set of elements in that are not in . Absolute complement Definition If is a set, then the absolute complement of (or simply the complement of ) is the set of elements not in (within a larger set that is implicitly defined). In other words, let be a set that contains all the elements under study; if there is no need to mention , either because it has been previously specified, or it is obvious and unique, then the absolute complement of is the relative complement of in : A^c= U \setminus A = \. The absolute complement of is usually denoted by A^c. Other ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Structure Four
A structure is an arrangement and organization of interrelated elements in a material object or system, or the object or system so organized. Material structures include man-made objects such as buildings and machines and natural objects such as organism, biological organisms, minerals and chemical substance, chemicals. Abstract structures include data structures in computer science and musical form. Types of structure include a hierarchy (a cascade of one-to-many relationships), a Complex network, network featuring many-to-many Link (geometry), links, or a lattice (order), lattice featuring connections between components that are neighbors in space. Load-bearing Buildings, aircraft, skeletons, Ant colony, anthills, beaver dams, bridges and salt domes are all examples of Structural load, load-bearing structures. The results of construction are divided into buildings and nonbuilding structure, non-building structures, and make up the infrastructure of a human society. Built str ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Set Complement
In set theory, the complement of a set , often denoted by A^c (or ), is the set of elements not in . When all elements in the universe, i.e. all elements under consideration, are considered to be members of a given set , the absolute complement of is the set of elements in that are not in . The relative complement of with respect to a set , also termed the set difference of and , written B \setminus A, is the set of elements in that are not in . Absolute complement Definition If is a set, then the absolute complement of (or simply the complement of ) is the set of elements not in (within a larger set that is implicitly defined). In other words, let be a set that contains all the elements under study; if there is no need to mention , either because it has been previously specified, or it is obvious and unique, then the absolute complement of is the relative complement of in : A^c= U \setminus A = \. The absolute complement of is usually denoted by A^c. Other ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mathematical Morphology
Mathematical morphology (MM) is a theory and technique for the analysis and processing of Geometry, geometrical structures, based on set theory, lattice theory, topology, and random functions. MM is most commonly applied to digital images, but it can be employed as well on Graph (discrete mathematics), graphs, polygon mesh, surface meshes, Solid geometry, solids, and many other spatial structures. Topology, Topological and Geometry, geometrical continuum (theory), continuous-space concepts such as size, shape, convex set, convexity, Connectedness, connectivity, and geodesic distance, were introduced by MM on both continuous and discrete spaces. MM is also the foundation of morphological image processing, which consists of a set of operators that transform images according to the above characterizations. The basic morphological operators are Erosion (morphology), erosion, Dilation (morphology), dilation, Opening (morphology), opening and Closing (morphology), closing. MM was orig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |