|
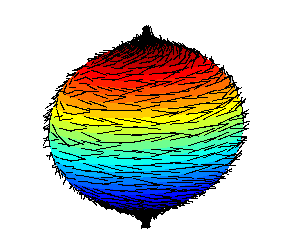
Hairy Ball Theorem
The hairy ball theorem of algebraic topology (sometimes called the hedgehog theorem in Europe) states that there is no nonvanishing continuous tangent vector field on even-dimensional ''n''-spheres. For the ordinary sphere, or 2‑sphere, if ''f'' is a continuous function that assigns a vector in R3 to every point ''p'' on a sphere such that ''f''(''p'') is always tangent to the sphere at ''p'', then there is at least one pole, a point where the field vanishes (a ''p'' such that ''f''(''p'') = 0). The theorem was first proved by Henri Poincaré for the 2-sphere in 1885, and extended to higher dimensions in 1912 by Luitzen Egbertus Jan Brouwer. The theorem has been expressed colloquially as "you can't comb a hairy ball flat without creating a cowlick" or "you can't comb the hair on a coconut". Counting zeros Every zero of a vector field has a (non-zero) " index", and it can be shown that the sum of all of the indices at all of the zeros must be two, because the Euler char ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hairy Ball
The hairy ball theorem of algebraic topology (sometimes called the hedgehog theorem in Europe) states that there is no nonvanishing continuous tangent vector field on even-dimensional ''n''-spheres. For the ordinary sphere, or 2‑sphere, if ''f'' is a continuous function that assigns a vector in R3 to every point ''p'' on a sphere such that ''f''(''p'') is always tangent to the sphere at ''p'', then there is at least one pole, a point where the field vanishes (a ''p'' such that ''f''(''p'') = 0). The theorem was first proved by Henri Poincaré for the 2-sphere in 1885, and extended to higher dimensions in 1912 by Luitzen Egbertus Jan Brouwer. The theorem has been expressed colloquially as "you can't comb a hairy ball flat without creating a cowlick" or "you can't comb the hair on a coconut". Counting zeros Every zero of a vector field has a (non-zero) "index", and it can be shown that the sum of all of the indices at all of the zeros must be two, because the Euler charact ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torus
In geometry, a torus (plural tori, colloquially donut or doughnut) is a surface of revolution generated by revolving a circle in three-dimensional space about an axis that is coplanar with the circle. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a spindle torus. If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid. Real-world objects that approximate a torus of revolution include swim rings, inner tubes and ringette rings. Eyeglass lenses that combine spherical and cylindrical correction are toric lenses. A torus should not be confused with a '' solid torus'', which is formed by r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Functions (mathematics)
In mathematics, a function from a set to a set assigns to each element of exactly one element of .; the words map, mapping, transformation, correspondence, and operator are often used synonymously. The set is called the domain of the function and the set is called the codomain of the function.Codomain ''Encyclopedia of Mathematics'Codomain. ''Encyclopedia of Mathematics''/ref> The earliest known approach to the notion of function can be traced back to works of Persian mathematicians Al-Biruni and Sharaf al-Din al-Tusi. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a ''function'' of time. Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the 19 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homotopic
In topology, a branch of mathematics, two continuous functions from one topological space to another are called homotopic (from grc, ὁμός "same, similar" and "place") if one can be "continuously deformed" into the other, such a deformation being called a homotopy (, ; , ) between the two functions. A notable use of homotopy is the definition of homotopy groups and cohomotopy groups, important invariants in algebraic topology. In practice, there are technical difficulties in using homotopies with certain spaces. Algebraic topologists work with compactly generated spaces, CW complexes, or spectra. Formal definition Formally, a homotopy between two continuous functions ''f'' and ''g'' from a topological space ''X'' to a topological space ''Y'' is defined to be a continuous function H: X \times ,1\to Y from the product of the space ''X'' with the unit interval , 1to ''Y'' such that H(x,0) = f(x) and H(x,1) = g(x) for all x \in X. If we think of the second p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism of smooth manifolds. It is an invertible function that maps one differentiable manifold to another such that both the function and its inverse are differentiable. Definition Given two manifolds M and N, a differentiable map f \colon M \rightarrow N is called a diffeomorphism if it is a bijection and its inverse f^ \colon N \rightarrow M is differentiable as well. If these functions are r times continuously differentiable, f is called a C^r-diffeomorphism. Two manifolds M and N are diffeomorphic (usually denoted M \simeq N) if there is a diffeomorphism f from M to N. They are C^r-diffeomorphic if there is an r times continuously differentiable bijective map between them whose inverse is also r times continuously differentiable. Diffeomorphisms of subsets of manifolds Given a subset X of a manifold M and a subset Y of a manifold N, a function f:X\to Y is said to be smooth if for all p in X there is a neighbor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
One-parameter Group
In mathematics, a one-parameter group or one-parameter subgroup usually means a continuous group homomorphism :\varphi : \mathbb \rightarrow G from the real line \mathbb (as an additive group) to some other topological group G. If \varphi is injective then \varphi(\mathbb), the image, will be a subgroup of G that is isomorphic to \mathbb as an additive group. One-parameter groups were introduced by Sophus Lie in 1893 to define infinitesimal transformations. According to Lie, an ''infinitesimal transformation'' is an infinitely small transformation of the one-parameter group that it generates. It is these infinitesimal transformations that generate a Lie algebra that is used to describe a Lie group of any dimension. The action of a one-parameter group on a set is known as a flow. A smooth vector field on a manifold, at a point, induces a ''local flow'' - a one parameter group of local diffeomorphisms, sending points along integral curves of the vector field. The local flow of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Identity Mapping
Graph of the identity function on the real numbers In mathematics, an identity function, also called an identity relation, identity map or identity transformation, is a function that always returns the value that was used as its argument, unchanged. That is, when is the identity function, the equality is true for all values of to which can be applied. Definition Formally, if is a set, the identity function on is defined to be a function with as its domain and codomain, satisfying In other words, the function value in the codomain is always the same as the input element in the domain . The identity function on is clearly an injective function as well as a surjective function, so it is bijective. The identity function on is often denoted by . In set theory, where a function is defined as a particular kind of binary relation, the identity function is given by the identity relation, or ''diagonal'' of . Algebraic properties If is any function, then we have (whe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homology (mathematics)
In mathematics, homology is a general way of associating a sequence of algebraic objects, such as abelian groups or modules, with other mathematical objects such as topological spaces. Homology groups were originally defined in algebraic topology. Similar constructions are available in a wide variety of other contexts, such as abstract algebra, groups, Lie algebras, Galois theory, and algebraic geometry. The original motivation for defining homology groups was the observation that two shapes can be distinguished by examining their holes. For instance, a circle is not a disk because the circle has a hole through it while the disk is solid, and the ordinary sphere is not a circle because the sphere encloses a two-dimensional hole while the circle encloses a one-dimensional hole. However, because a hole is "not there", it is not immediately obvious how to define a hole or how to distinguish different kinds of holes. Homology was originally a rigorous mathematical method for defi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lefschetz Number
In mathematics, the Lefschetz fixed-point theorem is a formula that counts the fixed points of a continuous mapping from a compact topological space X to itself by means of traces of the induced mappings on the homology groups of X. It is named after Solomon Lefschetz, who first stated it in 1926. The counting is subject to an imputed multiplicity at a fixed point called the fixed-point index. A weak version of the theorem is enough to show that a mapping without ''any'' fixed point must have rather special topological properties (like a rotation of a circle). Formal statement For a formal statement of the theorem, let :f\colon X \rightarrow X\, be a continuous map from a compact triangulable space X to itself. Define the Lefschetz number \Lambda_f of f by :\Lambda_f:=\sum_(-1)^k\mathrm(f_*, H_k(X,\Q)), the alternating (finite) sum of the matrix traces of the linear maps induced by f on H_k(X,\Q), the singular homology groups of X with rational coefficients. A simple versi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Betti Number
In algebraic topology, the Betti numbers are used to distinguish topological spaces based on the connectivity of ''n''-dimensional simplicial complexes. For the most reasonable finite-dimensional spaces (such as compact manifolds, finite simplicial complexes or CW complexes), the sequence of Betti numbers is 0 from some point onward (Betti numbers vanish above the dimension of a space), and they are all finite. The ''n''th Betti number represents the rank of the ''n''th homology group, denoted ''H''''n'', which tells us the maximum number of cuts that can be made before separating a surface into two pieces or 0-cycles, 1-cycles, etc. For example, if H_n(X) \cong 0 then b_n(X) = 0, if H_n(X) \cong \mathbb then b_n(X) = 1, if H_n(X) \cong \mathbb \oplus \mathbb then b_n(X) = 2, if H_n(X) \cong \mathbb \oplus \mathbb\oplus \mathbb then b_n(X) = 3, etc. Note that only the ranks of infinite groups are considered, so for example if H_n(X) \cong \mathbb^k \oplus \mathbb/(2) , where \mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lefschetz Fixed-point Theorem
In mathematics, the Lefschetz fixed-point theorem is a formula that counts the fixed points of a continuous mapping from a compact topological space X to itself by means of traces of the induced mappings on the homology groups of X. It is named after Solomon Lefschetz, who first stated it in 1926. The counting is subject to an imputed multiplicity at a fixed point called the fixed-point index. A weak version of the theorem is enough to show that a mapping without ''any'' fixed point must have rather special topological properties (like a rotation of a circle). Formal statement For a formal statement of the theorem, let :f\colon X \rightarrow X\, be a continuous map from a compact triangulable space X to itself. Define the Lefschetz number \Lambda_f of f by :\Lambda_f:=\sum_(-1)^k\mathrm(f_*, H_k(X,\Q)), the alternating (finite) sum of the matrix traces of the linear maps induced by f on H_k(X,\Q), the singular homology groups of X with rational coefficients. A simple vers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |