|
Great Ellipse
150px, A spheroid A great ellipse is an ellipse passing through two points on a spheroid and having the same center as that of the spheroid. Equivalently, it is an ellipse on the surface of a spheroid and centered on the origin, or the curve formed by intersecting the spheroid by a plane through its center. For points that are separated by less than about a quarter of the circumference of the earth, about 10\,000\,\mathrm, the length of the great ellipse connecting the points is close (within one part in 500,000) to the geodesic distance. The great ellipse therefore is sometimes proposed as a suitable route for marine navigation. The great ellipse is special case of an earth section path. Introduction Assume that the spheroid, an ellipsoid of revolution, has an equatorial radius a and polar semi-axis b. Define the flattening f=(a-b)/a, the eccentricity e=\sqrt, and the second eccentricity e'=e/(1-f). Consider two points: A at (geographic) latitude \phi_1 and longitude \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great-circle Navigation
Great-circle navigation or orthodromic navigation (related to orthodromic course; from the Greek ''ορθóς'', right angle, and ''δρóμος'', path) is the practice of navigating a vessel (a ship or aircraft) along a great circle. Such routes yield the shortest distance between two points on the globe. Course The great circle path may be found using spherical trigonometry; this is the spherical version of the '' inverse geodetic problem''. If a navigator begins at ''P''1 = (φ1,λ1) and plans to travel the great circle to a point at point ''P''2 = (φ2,λ2) (see Fig. 1, φ is the latitude, positive northward, and λ is the longitude, positive eastward), the initial and final courses α1 and α2 are given by formulas for solving a spherical triangle :\begin \tan\alpha_1&=\frac,\\ \tan\alpha_2&=\frac,\\ \end where λ12 = λ2 − λ1In the article on great-circle distances, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhumb Line
In navigation, a rhumb line, rhumb (), or loxodrome is an arc crossing all meridians of longitude at the same angle, that is, a path with constant bearing as measured relative to true north. Introduction The effect of following a rhumb line course on the surface of a globe was first discussed by the Portuguese mathematician Pedro Nunes in 1537, in his ''Treatise in Defense of the Marine Chart'', with further mathematical development by Thomas Harriot in the 1590s. A rhumb line can be contrasted with a great circle, which is the path of shortest distance between two points on the surface of a sphere. On a great circle, the bearing to the destination point does not remain constant. If one were to drive a car along a great circle one would hold the steering wheel fixed, but to follow a rhumb line one would have to turn the wheel, turning it more sharply as the poles are approached. In other words, a great circle is locally "straight" with zero geodesic curvature, whereas a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
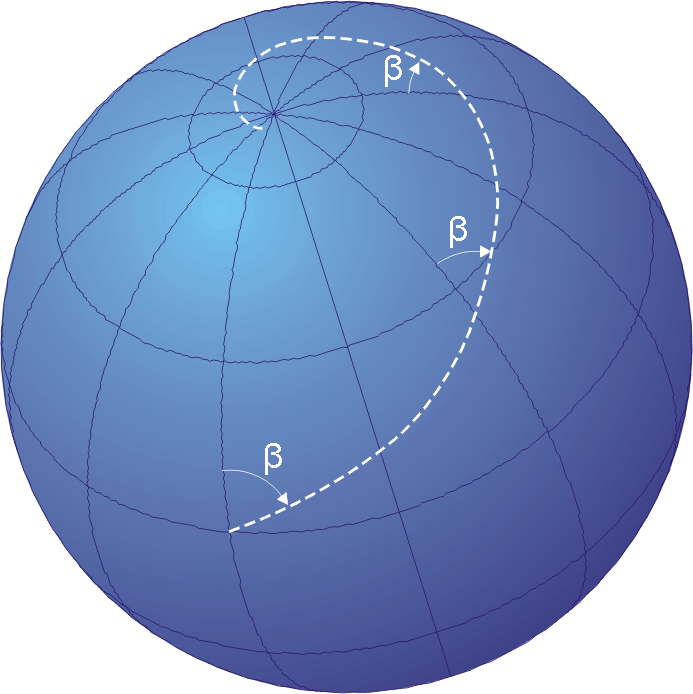
Geodesics On An Ellipsoid
The study of geodesics on an ellipsoid arose in connection with geodesy specifically with the solution of triangulation networks. The figure of the Earth is well approximated by an '' oblate ellipsoid'', a slightly flattened sphere. A ''geodesic'' is the shortest path between two points on a curved surface, analogous to a straight line on a plane surface. The solution of a triangulation network on an ellipsoid is therefore a set of exercises in spheroidal trigonometry . If the Earth is treated as a sphere, the geodesics are great circles (all of which are closed) and the problems reduce to ones in spherical trigonometry. However, showed that the effect of the rotation of the Earth results in its resembling a slightly oblate ellipsoid: in this case, the equator and the meridians are the only simple closed geodesics. Furthermore, the shortest path between two points on the equator does not necessarily run along the equator. Finally, if the ellipsoid is further perturbed to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Earth Section Paths
Earth section paths are plane curves defined by the intersection of an earth ellipsoid and a plane (ellipsoid plane sections). Common examples include the ''great ellipse'' (containing the center of the ellipsoid) and normal sections (containing an ellipsoid normal direction). Earth section paths are useful as approximate solutions for geodetic problems, the direct and inverse calculation of geographic distances. The rigorous solution of geodetic problems involves skew curves known as ''geodesics''. Inverse problem The inverse problem for earth sections is: given two points, P_1 and P_2 on the surface of the reference ellipsoid, find the length, s_, of the short arc of a spheroid section from P_1 to P_2 and also find the departure and arrival azimuths (angle from true north) of that curve, \alpha_1 and \alpha_2. The figure to the right illustrates the notation used here. Let P_k have geodetic latitude \phi_k and longitude \lambda_k (''k''=1,2). This problem is best solved u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Meridian Arc
In geodesy and navigation, a meridian arc is the curve between two points on the Earth's surface having the same longitude. The term may refer either to a segment of the meridian, or to its length. The purpose of measuring meridian arcs is to determine a figure of the Earth. One or more measurements of meridian arcs can be used to infer the shape of the reference ellipsoid that best approximates the geoid in the region of the measurements. Measurements of meridian arcs at several latitudes along many meridians around the world can be combined in order to approximate a ''geocentric ellipsoid'' intended to fit the entire world. The earliest determinations of the size of a spherical Earth required a single arc. Accurate survey work beginning in the 19th century required several arc measurements in the region the survey was to be conducted, leading to a proliferation of reference ellipsoids around the world. The latest determinations use astro-geodetic measurements and the method ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Meridian Arc
In geodesy and navigation, a meridian arc is the curve between two points on the Earth's surface having the same longitude. The term may refer either to a segment of the meridian, or to its length. The purpose of measuring meridian arcs is to determine a figure of the Earth. One or more measurements of meridian arcs can be used to infer the shape of the reference ellipsoid that best approximates the geoid in the region of the measurements. Measurements of meridian arcs at several latitudes along many meridians around the world can be combined in order to approximate a ''geocentric ellipsoid'' intended to fit the entire world. The earliest determinations of the size of a spherical Earth required a single arc. Accurate survey work beginning in the 19th century required several arc measurements in the region the survey was to be conducted, leading to a proliferation of reference ellipsoids around the world. The latest determinations use astro-geodetic measurements and the method ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great-circle Navigation
Great-circle navigation or orthodromic navigation (related to orthodromic course; from the Greek ''ορθóς'', right angle, and ''δρóμος'', path) is the practice of navigating a vessel (a ship or aircraft) along a great circle. Such routes yield the shortest distance between two points on the globe. Course The great circle path may be found using spherical trigonometry; this is the spherical version of the '' inverse geodetic problem''. If a navigator begins at ''P''1 = (φ1,λ1) and plans to travel the great circle to a point at point ''P''2 = (φ2,λ2) (see Fig. 1, φ is the latitude, positive northward, and λ is the longitude, positive eastward), the initial and final courses α1 and α2 are given by formulas for solving a spherical triangle :\begin \tan\alpha_1&=\frac,\\ \tan\alpha_2&=\frac,\\ \end where λ12 = λ2 − λ1In the article on great-circle distances, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latitude
In geography, latitude is a coordinate that specifies the north– south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north pole, with 0° at the Equator. Lines of constant latitude, or ''parallels'', run east–west as circles parallel to the equator. Latitude and ''longitude'' are used together as a coordinate pair to specify a location on the surface of the Earth. On its own, the term "latitude" normally refers to the ''geodetic latitude'' as defined below. Briefly, the geodetic latitude of a point is the angle formed between the vector perpendicular (or '' normal'') to the ellipsoidal surface from the point, and the plane of the equator. Background Two levels of abstraction are employed in the definitions of latitude and longitude. In the first step the physical surface is modeled by the geoid, a surface which approximates the mean sea level over the oce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Azimuth
An azimuth (; from ar, اَلسُّمُوت, as-sumūt, the directions) is an angular measurement in a spherical coordinate system. More specifically, it is the horizontal angle from a cardinal direction, most commonly north. Mathematically, the relative position vector from an observer ( origin) to a point of interest is projected perpendicularly onto a reference plane (the horizontal plane); the angle between the projected vector and a reference vector on the reference plane is called the azimuth. When used as a celestial coordinate, the azimuth is the horizontal direction of a star or other astronomical object in the sky. The star is the point of interest, the reference plane is the local area (e.g. a circular area with a 5 km radius at sea level) around an observer on planetary surface, Earth's surface, and the reference vector points to true north. The azimuth is the angle between the north vector and the star's vector on the horizontal plane In astronomy, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ellipse
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity e, a number ranging from e = 0 (the limiting case of a circle) to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola). An ellipse has a simple algebraic solution for its area, but only approximations for its perimeter (also known as circumference), for which integration is required to obtain an exact solution. Analytically, the equation of a standard ellipse centered at the origin with width 2a and height 2b is: : \frac+\frac = 1 . Assuming a \ge b, the foci are (\pm c, 0) for c = \sqrt. The standard parametric equation is: : (x,y) = (a\cos(t),b\sin(t)) \quad \text \quad 0\leq t\leq 2\pi. Ellip ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Earth Section Paths
Earth section paths are plane curves defined by the intersection of an earth ellipsoid and a plane (ellipsoid plane sections). Common examples include the ''great ellipse'' (containing the center of the ellipsoid) and normal sections (containing an ellipsoid normal direction). Earth section paths are useful as approximate solutions for geodetic problems, the direct and inverse calculation of geographic distances. The rigorous solution of geodetic problems involves skew curves known as ''geodesics''. Inverse problem The inverse problem for earth sections is: given two points, P_1 and P_2 on the surface of the reference ellipsoid, find the length, s_, of the short arc of a spheroid section from P_1 to P_2 and also find the departure and arrival azimuths (angle from true north) of that curve, \alpha_1 and \alpha_2. The figure to the right illustrates the notation used here. Let P_k have geodetic latitude \phi_k and longitude \lambda_k (''k''=1,2). This problem is best solved u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |