|
Great Complex Icosidodecahedron
In geometry, the great complex icosidodecahedron is a degenerate uniform star polyhedron In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting. Each polyhedron can contain either star polygon faces, star polygon vertex figures, .... It has 12 vertices, and 60 (doubled) edges, and 32 faces, 12 pentagrams and 20 triangles. All edges are doubled (making it degenerate), sharing 4 faces, but are considered as two overlapping edges as topological polyhedron. It can be constructed from a number of different vertex figures. As a compound The great complex icosidodecahedron can be considered a compound of the small stellated dodecahedron, , and great icosahedron, , sharing the same vertices and edges, while the second is hidden, being completely contained inside the first. {, , {, class=wikitable width=300 , + Compound polyhedron , , , , - align=center , Small s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a '' geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small Stellated Dodecahedron
In geometry, the small stellated dodecahedron is a Kepler-Poinsot polyhedron, named by Arthur Cayley, and with Schläfli symbol . It is one of four nonconvex regular polyhedra. It is composed of 12 pentagrammic faces, with five pentagrams meeting at each vertex. It shares the same vertex arrangement as the convex regular icosahedron. It also shares the same edge arrangement with the great icosahedron, with which it forms a degenerate uniform compound figure. It is the second of four stellations of the dodecahedron (including the original dodecahedron itself). The small stellated dodecahedron can be constructed analogously to the pentagram, its two-dimensional analogue, via the extension of the edges (1-faces) of the core polytope until a point is reached where they intersect. Topology If the pentagrammic faces are considered as 5 triangular faces, it shares the same surface topology as the pentakis dodecahedron, but with much taller isosceles triangle faces, with the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Complex Rhombicosidodecahedron
In geometry, the small complex rhombicosidodecahedron (also known as the small complex ditrigonal rhombicosidodecahedron) is a degenerate uniform star polyhedron. It has 62 faces (20 triangles, 12 pentagrams and 30 squares), 120 (doubled) edges and 20 vertices. All edges are doubled (making it degenerate), sharing 4 faces, but are considered as two overlapping edges as a topological polyhedron. It can be constructed from the vertex figure 3(5/2.4.3.4), thus making it also a cantellated great icosahedron. The "3" in front of this vertex figure indicates that each vertex in this degenerate polyhedron is in fact three coincident vertices. It may also be given the Schläfli symbol rr or t0,2. As a compound It can be seen as a compound of the small ditrigonal icosidodecahedron, U30, and the compound of five cubes. It is also a faceting of the dodecahedron. As a cantellation It can also be seen as a cantellation of the great icosahedron (or, equivalently, of the great stellated ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Rhombidodecadodecahedron
Complex commonly refers to: * Complexity, the behaviour of a system whose components interact in multiple ways so possible interactions are difficult to describe ** Complex system, a system composed of many components which may interact with each other * Complex (psychology), a core pattern of emotions etc. in the personal unconscious organized around a common theme such as power or status Complex may also refer to: Arts, entertainment and media * Complex (English band), formed in 1968, and their 1971 album ''Complex'' * Complex (band), a Japanese rock band * Complex (album), ''Complex'' (album), by Montaigne, 2019, and its title track * Complex (EP), ''Complex'' (EP), by Rifle Sport, 1985 * Complex (song), "Complex" (song), by Gary Numan, 1979 * Complex Networks, publisher of magazine ''Complex'', now online Biology * Protein–ligand complex, a complex of a protein bound with a ligand * Exosome complex, a multi-protein intracellular complex * Protein complex, a group of two or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small Complex Rhombicosidodecahedron
In geometry, the small complex rhombicosidodecahedron (also known as the small complex ditrigonal rhombicosidodecahedron) is a degenerate uniform star polyhedron. It has 62 faces (20 triangles, 12 pentagrams and 30 squares), 120 (doubled) edges and 20 vertices. All edges are doubled (making it degenerate), sharing 4 faces, but are considered as two overlapping edges as a topological polyhedron. It can be constructed from the vertex figure 3(5/2.4.3.4), thus making it also a cantellated great icosahedron. The "3" in front of this vertex figure indicates that each vertex in this degenerate polyhedron is in fact three coincident vertices. It may also be given the Schläfli symbol rr or t0,2. As a compound It can be seen as a compound of the small ditrigonal icosidodecahedron, U30, and the compound of five cubes. It is also a faceting of the dodecahedron. As a cantellation It can also be seen as a cantellation of the great icosahedron (or, equivalently, of the great s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small Complex Icosidodecahedron
In geometry, the small complex icosidodecahedron is a degenerate uniform star polyhedron. Its edges are doubled, making it degenerate. The star has 32 faces (20 triangles and 12 pentagons), 60 (doubled) edges and 12 vertices and 4 sharing faces. The faces in it are considered as two overlapping edges as topological polyhedron. A small complex icosidodecahedron can be constructed from a number of different vertex figures. A very similar figure emerges as a geometrical truncation of the great stellated dodecahedron, where the pentagram faces become doubly-wound pentagons ( --> ), making the internal pentagonal planes, and the three meeting at each vertex become triangles, making the external triangular planes. As a compound The small complex icosidodecahedron can be seen as a compound of the icosahedron and the great dodecahedron where all vertices are precise and edges coincide. The small complex icosidodecahedron resembles an icosahedron, because the great dodecahedron i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Complex Icosidodecahedron
In geometry, the great complex icosidodecahedron is a degenerate uniform star polyhedron In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting. Each polyhedron can contain either star polygon faces, star polygon vertex figures, .... It has 12 vertices, and 60 (doubled) edges, and 32 faces, 12 pentagrams and 20 triangles. All edges are doubled (making it degenerate), sharing 4 faces, but are considered as two overlapping edges as topological polyhedron. It can be constructed from a number of different vertex figures. As a compound The great complex icosidodecahedron can be considered a compound of the small stellated dodecahedron, , and great icosahedron, , sharing the same vertices and edges, while the second is hidden, being completely contained inside the first. {, , {, class=wikitable width=300 , + Compound polyhedron , , , , - align=center , Small s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
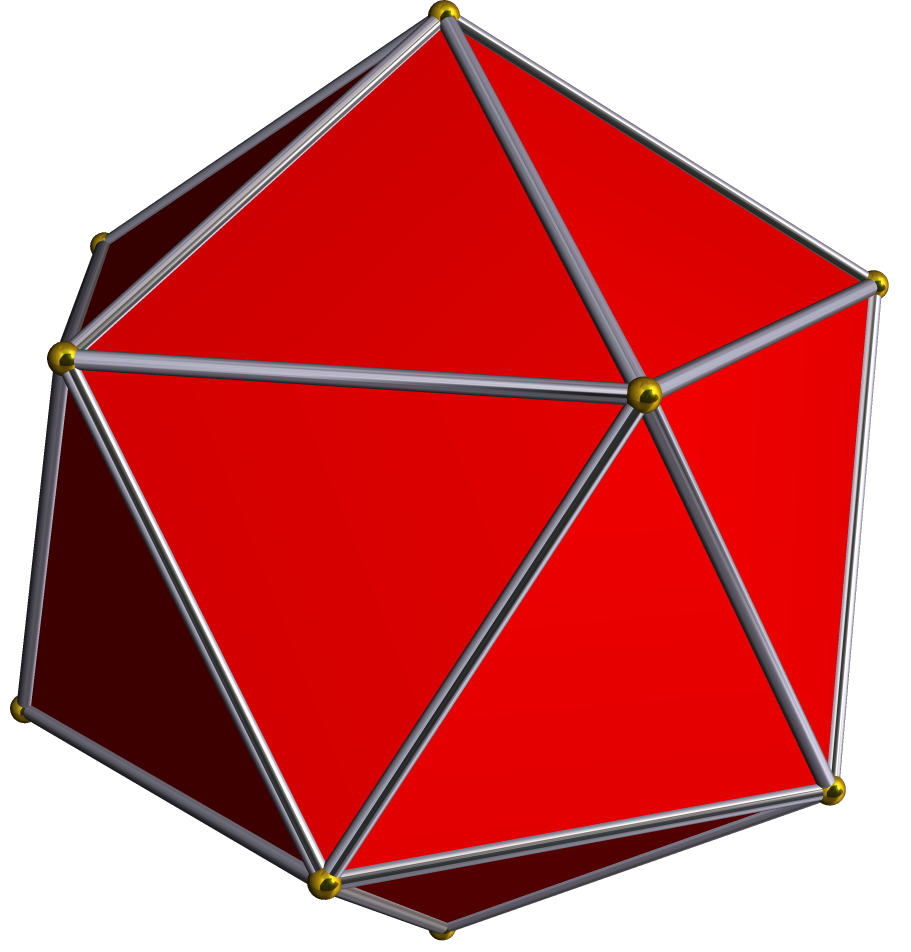
Great Icosahedron
In geometry, the great icosahedron is one of four Kepler–Poinsot polyhedra (nonconvex regular polyhedra), with Schläfli symbol and Coxeter-Dynkin diagram of . It is composed of 20 intersecting triangular faces, having five triangles meeting at each vertex in a pentagrammic sequence. The great icosahedron can be constructed analogously to the pentagram, its two-dimensional analogue, via the extension of the -dimensional simplex faces of the core -polytope (equilateral triangles for the great icosahedron, and line segments for the pentagram) until the figure regains regular faces. The grand 600-cell can be seen as its four-dimensional analogue using the same process. Images As a snub The ''great icosahedron'' can be constructed a uniform snub, with different colored faces and only tetrahedral symmetry: . This construction can be called a ''retrosnub tetrahedron'' or ''retrosnub tetratetrahedron'', similar to the snub tetrahedron symmetry of the icosahedron, as a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Star Polyhedron
In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting. Each polyhedron can contain either star polygon faces, star polygon vertex figures, or both. The complete set of 57 nonprismatic uniform star polyhedra includes the 4 regular ones, called the Kepler–Poinsot polyhedra, 5 quasiregular ones, and 48 semiregular ones. There are also two infinite sets of ''uniform star prisms'' and ''uniform star antiprisms''. Just as (nondegenerate) star polygons (which have polygon density greater than 1) correspond to circular polygons with overlapping tiles, star polyhedra that do not pass through the center have polytope density greater than 1, and correspond to spherical polyhedra with overlapping tiles; there are 47 nonprismatic such uniform star polyhedra. The remaining 10 nonprismatic uniform star polyhedra, those that pass through the center, are the hemipolyhedra as we ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small Stellated Dodecahedron
In geometry, the small stellated dodecahedron is a Kepler-Poinsot polyhedron, named by Arthur Cayley, and with Schläfli symbol . It is one of four nonconvex regular polyhedra. It is composed of 12 pentagrammic faces, with five pentagrams meeting at each vertex. It shares the same vertex arrangement as the convex regular icosahedron. It also shares the same edge arrangement with the great icosahedron, with which it forms a degenerate uniform compound figure. It is the second of four stellations of the dodecahedron (including the original dodecahedron itself). The small stellated dodecahedron can be constructed analogously to the pentagram, its two-dimensional analogue, via the extension of the edges (1-faces) of the core polytope until a point is reached where they intersect. Topology If the pentagrammic faces are considered as 5 triangular faces, it shares the same surface topology as the pentakis dodecahedron, but with much taller isosceles triangle faces, with the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Polyhedron
In geometry, a polyhedral compound is a figure that is composed of several polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram. The outer vertices of a compound can be connected to form a convex polyhedron called its convex hull. A compound is a facetting of its convex hull. Another convex polyhedron is formed by the small central space common to all members of the compound. This polyhedron can be used as the core for a set of stellations. Regular compounds A regular polyhedral compound can be defined as a compound which, like a regular polyhedron, is vertex-transitive, edge-transitive, and face-transitive. Unlike the case of polyhedra, this is not equivalent to the symmetry group acting transitively on its flags; the compound of two tetrahedra is the only regular compound with that property. There are five regular compounds of polyhedra: Best known is the regular compound of two tetrahedra, often called ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |






%2C_thick.png)