|
Global Optimisation
Global optimization is a branch of operations research, applied mathematics, and numerical analysis that attempts to find the global maximum and minimum, minimum or maximum of a function or a set of functions on a given set. It is usually described as a minimization problem because the maximization of the real-valued function g(x) is equivalent to the minimization of the function f(x):=(-1)\cdot g(x). Given a possibly nonlinear and non-convex continuous function f:\Omega\subset\mathbb^n\to\mathbb with the global minimum f^* and the set of all global minimizers X^* in \Omega, the standard minimization problem can be given as :\min_f(x), that is, finding f^* and a global minimizer in X^*; where \Omega is a (not necessarily convex) compact set defined by inequalities g_i(x)\geqslant0, i=1,\ldots,r. Global optimization is distinguished from local optimization by its focus on finding the minimum or maximum over the given set, as opposed to finding ''local'' minima or maxima. Finding ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Operations Research
Operations research () (U.S. Air Force Specialty Code: Operations Analysis), often shortened to the initialism OR, is a branch of applied mathematics that deals with the development and application of analytical methods to improve management and decision-making. Although the term management science is sometimes used similarly, the two fields differ in their scope and emphasis. Employing techniques from other mathematical sciences, such as mathematical model, modeling, statistics, and mathematical optimization, optimization, operations research arrives at optimal or near-optimal solutions to decision-making problems. Because of its emphasis on practical applications, operations research has overlapped with many other disciplines, notably industrial engineering. Operations research is often concerned with determining the extreme values of some real-world objective: the Maxima and minima, maximum (of profit, performance, or yield) or minimum (of loss, risk, or cost). Originating in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
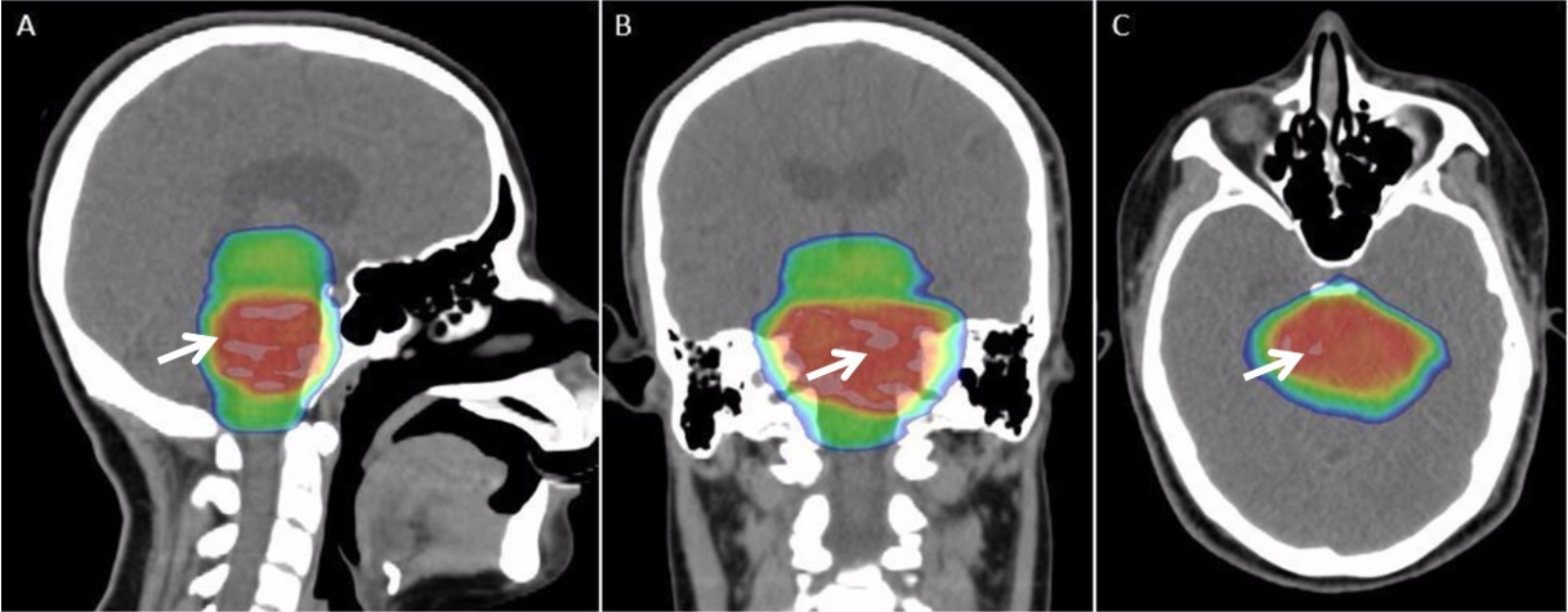
Radiation Therapy
Radiation therapy or radiotherapy (RT, RTx, or XRT) is a therapy, treatment using ionizing radiation, generally provided as part of treatment of cancer, cancer therapy to either kill or control the growth of malignancy, malignant cell (biology), cells. It is normally delivered by a linear particle accelerator. Radiation therapy may be cure, curative in a number of types of cancer if they are localized to one area of the body, and have not metastasis, spread to other parts. It may also be used as part of adjuvant therapy, to prevent tumor recurrence after surgery to remove a primary malignant tumor (for example, early stages of breast cancer). Radiation therapy is synergistic with chemotherapy, and has been used before, during, and after chemotherapy in susceptible cancers. The subspecialty of oncology concerned with radiotherapy is called radiation oncology. A physician who practices in this subspecialty is a radiation oncologist. Radiation therapy is commonly applied to the canc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Measurement Error
Observational error (or measurement error) is the difference between a measured value of a quantity and its unknown true value.Dodge, Y. (2003) ''The Oxford Dictionary of Statistical Terms'', OUP. Such errors are inherent in the measurement process; for example lengths measured with a ruler calibrated in whole centimeters will have a measurement error of several millimeters. The error or uncertainty of a measurement can be estimated, and is specified with the measurement as, for example, 32.3 ± 0.5 cm. Scientific observations are marred by two distinct types of errors, systematic errors on the one hand, and random, on the other hand. The effects of random errors can be mitigated by the repeated measurements. Constant or systematic errors on the contrary must be carefully avoided, because they arise from one or more causes which constantly act in the same way, and have the effect of always altering the result of the experiment in the same direction. They therefore alter the va ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Rounding Error
In computing, a roundoff error, also called rounding error, is the difference between the result produced by a given algorithm using exact arithmetic and the result produced by the same algorithm using finite-precision, rounded arithmetic. Rounding errors are due to inexactness in the representation of real numbers and the arithmetic operations done with them. This is a form of quantization error. When using approximation equations or algorithms, especially when using finitely many digits to represent real numbers (which in theory have infinitely many digits), one of the goals of numerical analysis is to estimate computation errors. Computation errors, also called numerical errors, include both truncation errors and roundoff errors. When a sequence of calculations with an input involving any roundoff error are made, errors may accumulate, sometimes dominating the calculation. In ill-conditioned problems, significant error may accumulate. In short, there are two major facets ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Tree (graph Theory)
In graph theory, a tree is an undirected graph in which any two vertices are connected by path, or equivalently a connected acyclic undirected graph. A forest is an undirected graph in which any two vertices are connected by path, or equivalently an acyclic undirected graph, or equivalently a disjoint union of trees. A directed tree, oriented tree,See .See . polytree,See . or singly connected networkSee . is a directed acyclic graph (DAG) whose underlying undirected graph is a tree. A polyforest (or directed forest or oriented forest) is a directed acyclic graph whose underlying undirected graph is a forest. The various kinds of data structures referred to as trees in computer science have underlying graphs that are trees in graph theory, although such data structures are generally rooted trees. A rooted tree may be directed, called a directed rooted tree, either making all its edges point away from the root—in which case it is called an arborescence or out-tree� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
State Space Search
State-space search is a process used in the field of computer science, including artificial intelligence (AI), in which successive configurations or ''states'' of an instance are considered, with the intention of finding a ''goal state'' with the desired property. Problems are often modelled as a state space, a set of ''states'' that a problem can be in. The set of states forms a graph where two states are connected if there is an ''operation'' that can be performed to transform the first state into the second. State-space search often differs from traditional computer science search methods because the state space is ''implicit'': the typical state-space graph is much too large to generate and store in memory. Instead, nodes are generated as they are explored, and typically discarded thereafter. A solution to a combinatorial search instance may consist of the goal state itself, or of a path from some ''initial state'' to the goal state. Representation In state-space searc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Combinatorial Optimization
Combinatorial optimization is a subfield of mathematical optimization that consists of finding an optimal object from a finite set of objects, where the set of feasible solutions is discrete or can be reduced to a discrete set. Typical combinatorial optimization problems are the travelling salesman problem ("TSP"), the minimum spanning tree problem ("MST"), and the knapsack problem. In many such problems, such as the ones previously mentioned, exhaustive search is not tractable, and so specialized algorithms that quickly rule out large parts of the search space or approximation algorithms must be resorted to instead. Combinatorial optimization is related to operations research, algorithm theory, and computational complexity theory. It has important applications in several fields, including artificial intelligence, machine learning, auction theory, software engineering, VLSI, applied mathematics and theoretical computer science. Applications Basic applications of combina ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Discrete Optimization
Discrete optimization is a branch of optimization in applied mathematics and computer science. As opposed to continuous optimization, some or all of the variables used in a discrete optimization problem are restricted to be discrete variables—that is, to assume only a discrete set of values, such as the integer An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...s. Branches Three notable branches of discrete optimization are:. * combinatorial optimization, which refers to problems on graphs, matroids and other discrete structures * integer programming * constraint programming These branches are all closely intertwined however, since many combinatorial optimization problems can be modeled as integer programs (e.g. shortest path) or constraint programs, any constraint pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Algorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can use Conditional (computer programming), conditionals to divert the code execution through various routes (referred to as automated decision-making) and deduce valid inferences (referred to as automated reasoning). In contrast, a Heuristic (computer science), heuristic is an approach to solving problems without well-defined correct or optimal results.David A. Grossman, Ophir Frieder, ''Information Retrieval: Algorithms and Heuristics'', 2nd edition, 2004, For example, although social media recommender systems are commonly called "algorithms", they actually rely on heuristics as there is no truly "correct" recommendation. As an e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Václav Chvátal
Václav (Vašek) Chvátal () is a Professor Emeritus in the Department of Computer Science and Software Engineering at Concordia University in Montreal, Quebec, Canada, and a visiting professor at Charles University in Prague. He has published extensively on topics in graph theory, combinatorics, and combinatorial optimization. Biography Chvátal was born in 1946 in Prague and educated in mathematics at Charles University in Prague, where he studied under the supervision of Zdeněk Hedrlín. He fled Czechoslovakia in 1968, three days after the Soviet invasion, and completed his Ph.D. in Mathematics at the University of Waterloo, under the supervision of Crispin St. J. A. Nash-Williams, in the fall of 1970. Subsequently, he took positions at McGill University (1971 and 1978–1986), Stanford University (1972 and 1974–1977), the Université de Montréal (1972–1974 and 1977–1978), and Rutgers University (1986–2004) before returning to Montreal for the Canada Research Chai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ralph E
Ralph (pronounced or ) is a male name of English origin, derived from the Old English ''Rædwulf'' and Old High German ''Radulf'', cognate with the Old Norse ''Raðulfr'' (''rað'' "counsel" and ''ulfr'' "wolf"). The most common forms are: * Ralph, the common variant form in English, which takes either of the given pronunciations. * Rafe, variant form which is less common; this spelling is always pronounced . * Raif, a very rare variant. Raif Rackstraw from H.M.S. Pinafore * Ralf, the traditional variant form in Dutch, German, Swedish, and Polish. * Ralfs, the traditional variant form in Latvian. * Raoul, the traditional variant form in French. * Raúl, the traditional variant form in Spanish. * Raul, the traditional variant form in Portuguese and Italian. * Raül, the traditional variant form in Catalan. * Rádhulbh, the traditional variant form in Irish. First name Middle Ages * Ralph the Timid (died 1057), pre-Conquest Norman earl of Hereford, England * Ralp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Convex Optimization
Convex optimization is a subfield of mathematical optimization that studies the problem of minimizing convex functions over convex sets (or, equivalently, maximizing concave functions over convex sets). Many classes of convex optimization problems admit polynomial-time algorithms, whereas mathematical optimization is in general NP-hard. Definition Abstract form A convex optimization problem is defined by two ingredients: * The ''objective function'', which is a real-valued convex function of ''n'' variables, f :\mathcal D \subseteq \mathbb^n \to \mathbb; * The ''feasible set'', which is a convex subset C\subseteq \mathbb^n. The goal of the problem is to find some \mathbf \in C attaining :\inf \. In general, there are three options regarding the existence of a solution: * If such a point ''x''* exists, it is referred to as an ''optimal point'' or ''solution''; the set of all optimal points is called the ''optimal set''; and the problem is called ''solvable''. * If f is unbou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |