|
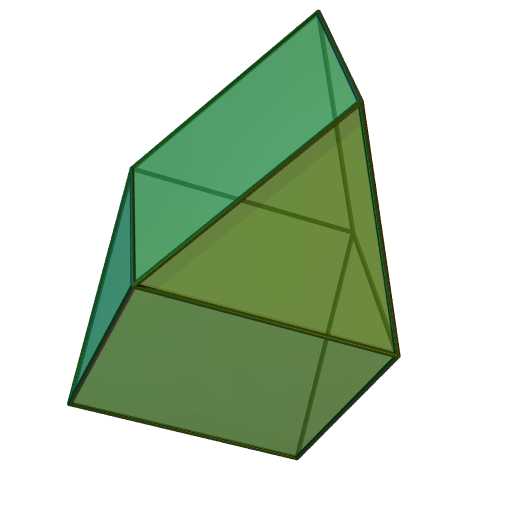
Gyrobicupola
In geometry, a bicupola is a solid formed by connecting two cupolae on their bases. There are two classes of bicupola because each cupola (bicupola half) is bordered by alternating triangles and squares. If similar faces are attached together the result is an ''orthobicupola''; if squares are attached to triangles it is a ''gyrobicupola''. Cupolae and bicupolae categorically exist as infinite sets of polyhedra, just like the pyramids, bipyramids, prisms, and trapezohedra. Six bicupolae have regular polygon faces: triangular, square and pentagonal ortho- and gyrobicupolae. The triangular gyrobicupola is an Archimedean solid, the cuboctahedron; the other five are Johnson solids. Bicupolae of higher order can be constructed if the flank faces are allowed to stretch into rectangles and isosceles triangles. Bicupolae are special in having four faces on every vertex. This means that their dual polyhedra will have all quadrilateral faces. The best known example is the rhombic dode ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cupola (geometry)
In geometry, a cupola is a solid formed by joining two polygons, one (the base) with twice as many edges as the other, by an alternating band of isosceles triangles and rectangles. If the triangles are equilateral and the rectangles are squares, while the base and its opposite face are regular polygons, the triangular, square, and pentagonal cupolae all count among the Johnson solids, and can be formed by taking sections of the cuboctahedron, rhombicuboctahedron, and rhombicosidodecahedron, respectively. A cupola can be seen as a prism where one of the polygons has been collapsed in half by merging alternate vertices. A cupola can be given an extended Schläfli symbol representing a regular polygon joined by a parallel of its truncation, or Cupolae are a subclass of the prismatoids. Its dual contains a shape that is sort of a weld between half of an -sided trapezohedron and a -sided pyramid. Examples The above-mentioned three polyhedra are the only non-trivial convex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johnson Solid
In geometry, a Johnson solid is a strictly convex polyhedron each face of which is a regular polygon. There is no requirement that isohedral, each face must be the same polygon, or that the same polygons join around each Vertex (geometry), vertex. An example of a Johnson solid is the square-based Pyramid (geometry), pyramid with equilateral sides (square pyramid, ); it has 1 square face and 4 triangular faces. Some authors require that the solid not be uniform polyhedron, uniform (i.e., not Platonic solid, Archimedean solid, prism (geometry), uniform prism, or uniform antiprism) before they refer to it as a “Johnson solid”. As in any strictly convex solid, at least three faces meet at every vertex, and the total of their angles is less than 360 degrees. Since a regular polygon has angles at least 60 degrees, it follows that at most five faces meet at any vertex. The pentagonal pyramid () is an example that has a degree-5 vertex. Although there is no obvious restriction tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cuboctahedron
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral. Its dual polyhedron is the rhombic dodecahedron. The cuboctahedron was probably known to Plato: Heron's ''Definitiones'' quotes Archimedes as saying that Plato knew of a solid made of 8 triangles and 6 squares. Synonyms *''Vector Equilibrium'' (Buckminster Fuller) because its center-to-vertex radius equals its edge length (it has radial equilateral symmetry). Fuller also called a cuboctahedron built of rigid struts and flexible vertices a ''jitterbug''; this object can be progressively transformed into an icosahedron, octahedron, and tetrahedron by folding along the diagonals of its square sid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedean Solid
In geometry, an Archimedean solid is one of the 13 solids first enumerated by Archimedes. They are the convex uniform polyhedra composed of regular polygons meeting in identical vertices, excluding the five Platonic solids (which are composed of only one type of polygon), excluding the prisms and antiprisms, and excluding the pseudorhombicuboctahedron. They are a subset of the Johnson solids, whose regular polygonal faces do not need to meet in identical vertices. "Identical vertices" means that each two vertices are symmetric to each other: A global isometry of the entire solid takes one vertex to the other while laying the solid directly on its initial position. observed that a 14th polyhedron, the elongated square gyrobicupola (or pseudo-rhombicuboctahedron), meets a weaker definition of an Archimedean solid, in which "identical vertices" means merely that the faces surrounding each vertex are of the same types (i.e. each vertex looks the same from close up), so only a lo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trapezo-rhombic Dodecahedron
In geometry, the trapezo-rhombic dodecahedron or rhombo-trapezoidal dodecahedron is a convex dodecahedron with 6 rhombic and 6 trapezoidal faces. It has symmetry. A concave form can be constructed with an identical net, seen as excavating trigonal trapezohedra from the top and bottom. Construction This polyhedron could be constructed by taking a tall uniform hexagonal prism, and making 3 angled cuts on the top and bottom. The trapezoids represent what remains of the original prism sides, and the 6 rhombi a result of the top and bottom cuts. Space-filling tessellation A space-filling tessellation, the trapezo-rhombic dodecahedral honeycomb, can be made by translated copies of this cell. Each "layer" is a hexagonal tiling, or a rhombille tiling, and alternate layers are connected by shifting their centers and rotating each polyhedron so the rhombic faces match up. :: In the special case that the long sides of the trapezoids equals twice the length of the short sides, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Orthobicupola
In geometry, the triangular orthobicupola is one of the Johnson solids (). As the name suggests, it can be constructed by attaching two triangular cupolas () along their bases. It has an equal number of squares and triangles at each vertex; however, it is not vertex-transitive. It is also called an ''anticuboctahedron'', ''twisted cuboctahedron'' or ''disheptahedron''. It is also a canonical polyhedron. The ''triangular orthobicupola'' is the first in an infinite set of orthobicupolae. Relation to cuboctahedra The ''triangular orthobicupola'' has a superficial resemblance to the cuboctahedron, which would be known as the ''triangular gyrobicupola'' in the nomenclature of Johnson solids — the difference is that the two triangular cupolas which make up the triangular orthobicupola are joined so that pairs of matching sides abut (hence, "ortho"); the cuboctahedron is joined so that triangles abut squares and vice versa. Given a triangular orthobicupola, a 60-degree rotati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Self-dual Polyhedron
In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron. Duality preserves the symmetries of a polyhedron. Therefore, for many classes of polyhedra defined by their symmetries, the duals belong to a corresponding symmetry class. For example, the regular polyhedrathe (convex) Platonic solids and (star) Kepler–Poinsot polyhedraform dual pairs, where the regular tetrahedron is self-dual. The dual of an isogonal polyhedron (one in which any two vertices are equivalent under symmetries of the polyhedron) is an isohedral polyhedron (one in which any two faces are equivalent .., and vice vers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthobifastigium
In geometry, the orthobifastigium (digonal ortho bicupola), is formed by gluing together two triangular prisms on their square faces, but without twisting. With regular faces, it has coplanar faces, so it is a limiting case of a Johnson solid. More generally the square can be isosceles trapezoids. It is topologically a self-dual polyhedron and can also be called an elongated octahedron and ''self-dual octahedron''. These polyhedra resemble the dual gyrobifastigium in that both shapes have eight vertices and eight faces, with the faces forming a belt of four quadrilaterals separating two pairs of triangles from each other. However, in the dual gyrobifastigium the two pairs of triangles are twisted with respect to each other while in the ''orthobifastigium'' they are not. Regular-faced It can be made with regular faces, squares and triangles, but the triangles will be coplanar. See also * Elongated octahedron In geometry, an elongated octahedron is a polyhedron with 8 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Digonal Orthobicupola
In geometry, the orthobifastigium (digonal ortho bicupola), is formed by gluing together two triangular prisms on their square faces, but without twisting. With regular faces, it has coplanar faces, so it is a limiting case of a Johnson solid. More generally the square can be isosceles trapezoids. It is topologically a self-dual polyhedron and can also be called an elongated octahedron and ''self-dual octahedron''. These polyhedra resemble the dual gyrobifastigium in that both shapes have eight vertices and eight faces, with the faces forming a belt of four quadrilaterals separating two pairs of triangles from each other. However, in the dual gyrobifastigium the two pairs of triangles are twisted with respect to each other while in the ''orthobifastigium'' they are not. Regular-faced It can be made with regular faces, squares and triangles, but the triangles will be coplanar. See also * Elongated octahedron In geometry, an elongated octahedron is a polyhedron with 8 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Spherical Symmetry Groups
Finite spherical symmetry groups are also called point groups in three dimensions. There are five fundamental symmetry classes which have triangular fundamental domains: dihedral, cyclic, tetrahedral, octahedral, and icosahedral symmetry. This article lists the groups by Schoenflies notation, Coxeter notation, orbifold notation, and order. John Conway uses a variation of the Schoenflies notation, based on the groups' quaternion algebraic structure, labeled by one or two upper case letters, and whole number subscripts. The group order is defined as the subscript, unless the order is doubled for symbols with a plus or minus, "±", prefix, which implies a central inversion. Hermann–Mauguin notation (International notation) is also given. The crystallography groups, 32 in total, are a subset with element orders 2, 3, 4 and 6.Sands, 1993 Involutional symmetry There are four involutional groups: no symmetry (C1), reflection symmetry (Cs), 2-fold rotational symmetry (C2), and cent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dodecahedron
In geometry, a dodecahedron (Greek , from ''dōdeka'' "twelve" + ''hédra'' "base", "seat" or "face") or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120. Some dodecahedra have the same combinatorial structure as the regular dodecahedron (in terms of the graph formed by its vertices and edges), but their pentagonal faces are not regular: The pyritohedron, a common crystal form in pyrite, has pyritohedral symmetry, while the tetartoid has tetrahedral symmetry. The rhombic dodecahedron can be seen as a limiting case of the pyritohedron, and it has octahedral symmetry. The elongated dodecahedron and trapezo-rhombic dodecahedron variations, along with the rhombic dodecahedra, are space-filling. There ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Orthobicupola
In geometry, the triangular orthobicupola is one of the Johnson solids (). As the name suggests, it can be constructed by attaching two triangular cupolas () along their bases. It has an equal number of squares and triangles at each vertex; however, it is not vertex-transitive. It is also called an ''anticuboctahedron'', ''twisted cuboctahedron'' or ''disheptahedron''. It is also a canonical polyhedron. The ''triangular orthobicupola'' is the first in an infinite set of orthobicupolae. Relation to cuboctahedra The ''triangular orthobicupola'' has a superficial resemblance to the cuboctahedron, which would be known as the ''triangular gyrobicupola'' in the nomenclature of Johnson solids — the difference is that the two triangular cupolas which make up the triangular orthobicupola are joined so that pairs of matching sides abut (hence, "ortho"); the cuboctahedron is joined so that triangles abut squares and vice versa. Given a triangular orthobicupola, a 60-degree rotati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |