|
Graph Center
The center (or Jordan center Wasserman, Stanley, and Faust, Katherine (1994), ''Social Network Analysis: Methods and Applications'', page 185. Cambridge: Cambridge University Press. ) of a graph is the set of all vertices of minimum eccentricity, that is, the set of all vertices ''u'' where the greatest distance ''d''(''u'',''v'') to other vertices ''v'' is minimal. Equivalently, it is the set of vertices with eccentricity equal to the graph's radius. Thus vertices in the center (central points) minimize the maximal distance from other points in the graph. This is also known as the vertex 1-center problem and can be extended to the vertex k-center problem. Finding the center of a graph is useful in facility location problems where the goal is to minimize the worst-case distance to the facility. For example, placing a hospital at a central point reduces the longest distance the ambulance has to travel. The center can be found using the Floyd–Warshall algorithm.Warshall, St ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Camille Jordan
Marie Ennemond Camille Jordan (; 5 January 1838 – 22 January 1922) was a French mathematician, known both for his foundational work in group theory and for his influential ''Cours d'analyse''. Biography Jordan was born in Lyon and educated at the École polytechnique. He was an engineer by profession; later in life he taught at the École polytechnique and the Collège de France, where he had a reputation for eccentric choices of notation. He is remembered now by name in a number of results: * The Jordan curve theorem, a topological result required in complex analysis * The Jordan normal form and the Jordan matrix in linear algebra * In mathematical analysis, Jordan measure (or ''Jordan content'') is an area measure that predates measure theory * In group theory, the Jordan–Hölder theorem on composition series is a basic result. * Jordan's theorem on finite linear groups Jordan's work did much to bring Galois theory into the mainstream. He also investigated the Mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Wasserman, Stanley
Stanley Wasserman (born August 29, 1951) is an American statistician and prior to retirement was the Rudy Professor of Statistics, Psychology, and Sociology at Indiana University Bloomington and the Academic Supervisor of the International laboratory for Applied Network Research at Moscow's National Research University – Higher School of Economics (since 2014). He is known for his work on social network analysis, mathematical sociology, network science and multidimensional networks. In 2017 Wasserman launched the Master's program 'Applied statistics with Network Analysis' at National Research University – Higher School of Economics. Biography Born in Louisville, Kentucky, Wasserman obtained his BSc in economics from the University of Pennsylvania in 1973, as well as his MA in Business & Applied Economics. He then moved to Harvard University, where he obtained his MA in Statistics in 1974, and his PhD in Statistics in 1977 with the thesis, entitled "Stochastic Models for Directe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Graph (discrete Mathematics)
In discrete mathematics, particularly in graph theory, a graph is a structure consisting of a Set (mathematics), set of objects where some pairs of the objects are in some sense "related". The objects are represented by abstractions called ''Vertex (graph theory), vertices'' (also called ''nodes'' or ''points'') and each of the related pairs of vertices is called an ''edge'' (also called ''link'' or ''line''). Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges. The edges may be directed or undirected. For example, if the vertices represent people at a party, and there is an edge between two people if they shake hands, then this graph is undirected because any person ''A'' can shake hands with a person ''B'' only if ''B'' also shakes hands with ''A''. In contrast, if an edge from a person ''A'' to a person ''B'' means that ''A'' owes money to ''B'', then this graph is directed, because owing mon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Eccentricity (graph Theory)
In the mathematical field of graph theory, the distance between two vertices in a graph is the number of edges in a shortest path (also called a graph geodesic) connecting them. This is also known as the geodesic distance or shortest-path distance. Notice that there may be more than one shortest path between two vertices. If there is no path connecting the two vertices, i.e., if they belong to different connected components, then conventionally the distance is defined as infinite. In the case of a directed graph the distance between two vertices and is defined as the length of a shortest directed path from to consisting of arcs, provided at least one such path exists. Notice that, in contrast with the case of undirected graphs, does not necessarily coincide with —so it is just a quasi-metric, and it might be the case that one is defined while the other is not. Related concepts A metric space defined over a set of points in terms of distances in a graph defined over ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Vertex K-center Problem
Vertex, vertices or vertexes may refer to: Science and technology Mathematics and computer science *Vertex (geometry), a point where two or more curves, lines, or edges meet *Vertex (computer graphics), a data structure that describes the position of a point *Vertex (curve), a point of a plane curve where the first derivative of curvature is zero *Vertex (graph theory), the fundamental unit of which graphs are formed * Vertex (topography), in a triangulated irregular network * Vertex of a representation, in finite group theory Physics * Vertex (physics), the reconstructed location of an individual particle collision *Vertex (optics), a point where the optical axis crosses an optical surface *Vertex function, describing the interaction between a photon and an electron Biology and anatomy *Vertex (anatomy), the highest point of the head *Vertex (urinary bladder), alternative name of the apex of urinary bladder *Vertex distance, the distance between the surface of the cornea of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Optimal Facility Location
The study of facility location problems (FLP), also known as location analysis, is a branch of operations research and computational geometry concerned with the optimal placement of facilities to minimize transportation costs while considering factors like avoiding placing hazardous materials near housing, and competitors' facilities. The techniques also apply to cluster analysis. Minimum facility location A simple facility location problem is the Weber problem, in which a single facility is to be placed, with the only optimization criterion being the minimization of the weighted sum of distances from a given set of point sites. More complex problems considered in this discipline include the placement of multiple facilities, constraints on the locations of facilities, and more complex optimization criteria. In a basic formulation, the facility location problem consists of a set of potential facility sites ''L'' where a facility can be opened, and a set of demand points ''D'' tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Floyd–Warshall Algorithm
In computer science, the Floyd–Warshall algorithm (also known as Floyd's algorithm, the Roy–Warshall algorithm, the Roy–Floyd algorithm, or the WFI algorithm) is an algorithm for finding shortest paths in a directed weighted graph with positive or negative edge weights (but with no negative cycles). See in particular Section 26.2, "The Floyd–Warshall algorithm", pp. 558–565 and Section 26.4, "A general framework for solving path problems in directed graphs", pp. 570–576. A single execution of the algorithm will find the lengths (summed weights) of shortest paths between all pairs of vertices. Although it does not return details of the paths themselves, it is possible to reconstruct the paths with simple modifications to the algorithm. Versions of the algorithm can also be used for finding the transitive closure of a relation R, or (in connection with the Schulze voting system) widest paths between all pairs of vertices in a weighted graph. History and nam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Closeness Centrality
In a connected graph, closeness centrality (or closeness) of a node is a measure of centrality in a network, calculated as the reciprocal of the sum of the length of the shortest paths between the node and all other nodes in the graph. Thus, the more central a node is, the ''closer'' it is to all other nodes. Closeness was defined by Bavelas (1950) as the reciprocal of the farness, that is: : C_B(x)= \frac, where d(y,x) is the distance (length of the shortest path) between vertices x and y. This unnormalised version of closeness is sometimes known as status. When speaking of closeness centrality, people usually refer to its normalized form which represents the average length of the shortest paths instead of their sum. It is generally given by the previous formula multiplied by N-1, where N is the number of nodes in the graph resulting in: : C(x)= \frac. The normalization of closeness simplifies the comparison of nodes in graphs of different sizes. For large graphs, the minu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
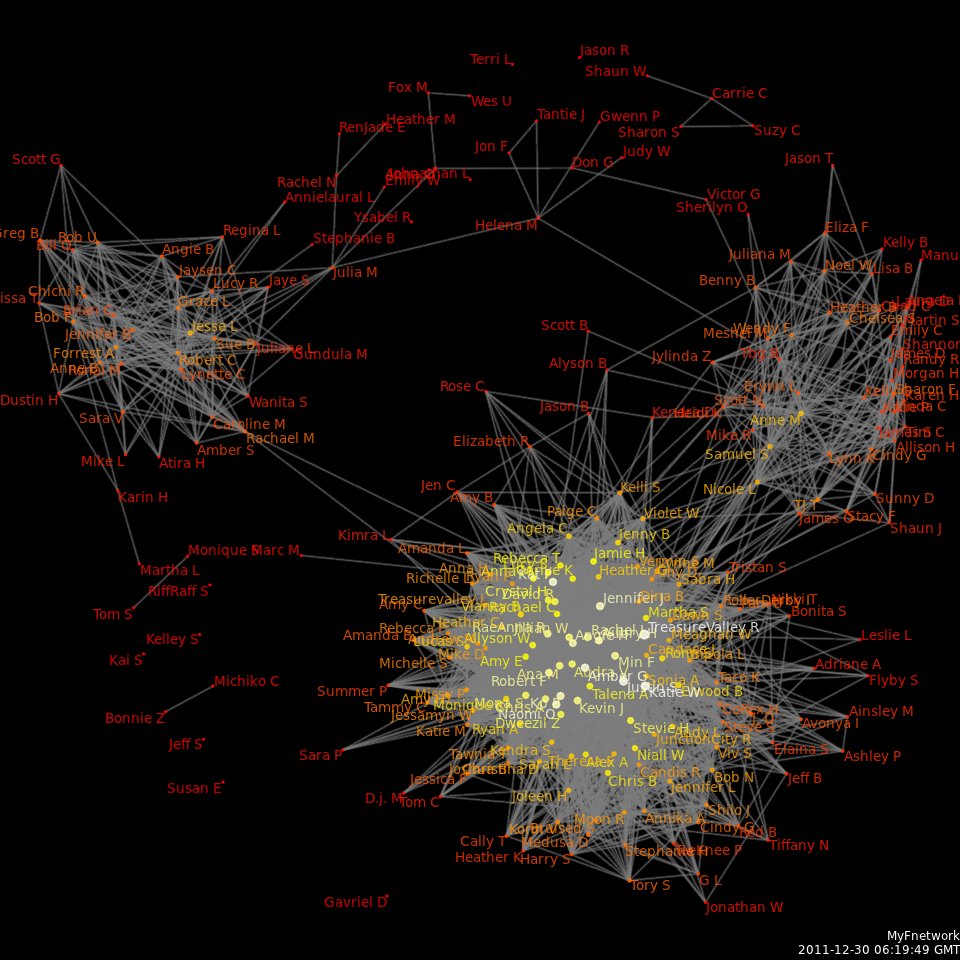
Social Network Analysis
Social network analysis (SNA) is the process of investigating social structures through the use of networks and graph theory. It characterizes networked structures in terms of ''nodes'' (individual actors, people, or things within the network) and the ''ties'', ''edges'', or ''links'' (relationships or interactions) that connect them. Examples of social structures commonly visualized through social network analysis include social media networks, meme proliferation, information circulation, friendship and acquaintance networks, business networks, knowledge networks, difficult working relationships, collaboration graphs, kinship, disease transmission, and sexual relationships. These networks are often visualized through '' sociograms'' in which nodes are represented as points and ties are represented as lines. These visualizations provide a means of qualitatively assessing networks by varying the visual representation of their nodes and edges to reflect attributes of inter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |